comm.gpu.PSKDemodulator

Demodulate signals using M-ary PSK method with GPU

To use this object, you must install Parallel Computing Toolbox™ and have access to a supported GPU. If the host computer has a GPU configured, processing uses the GPU. Otherwise, processing uses the CPU. For more information about GPUs, see GPU Computing (Parallel Computing Toolbox).

Description

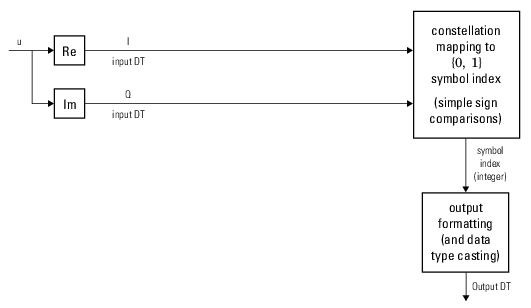
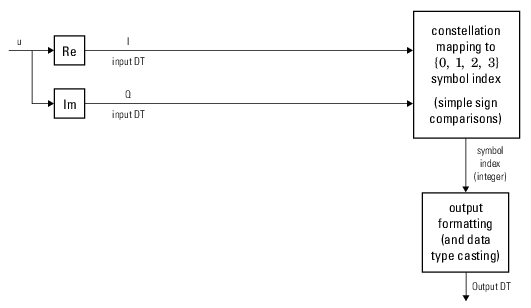
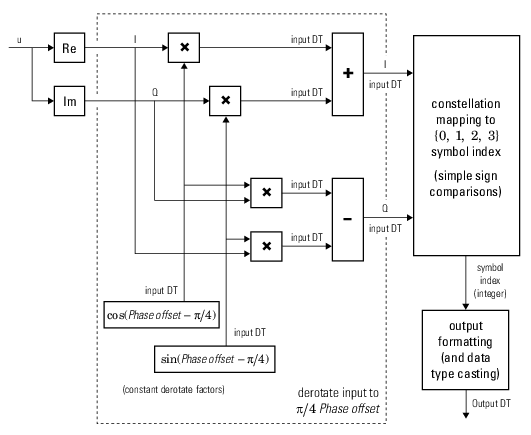
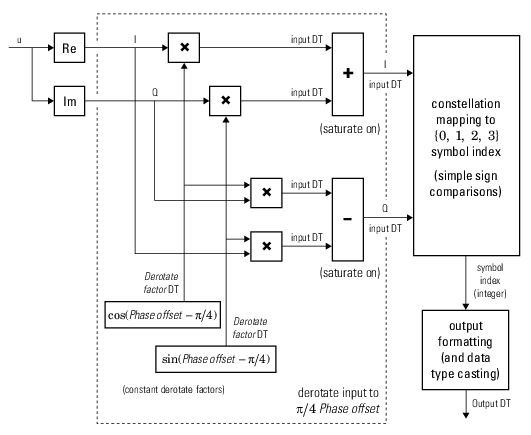
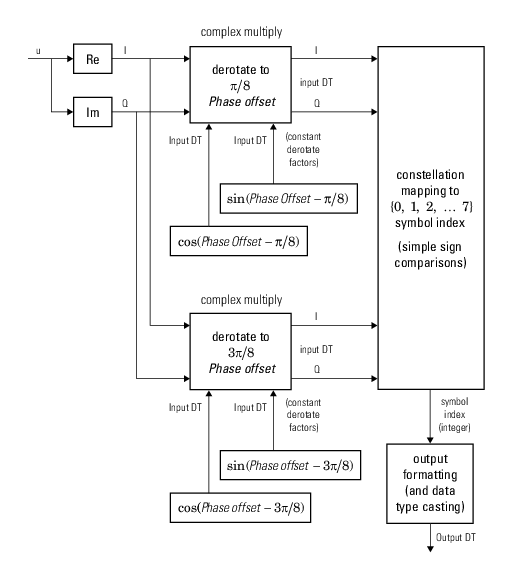
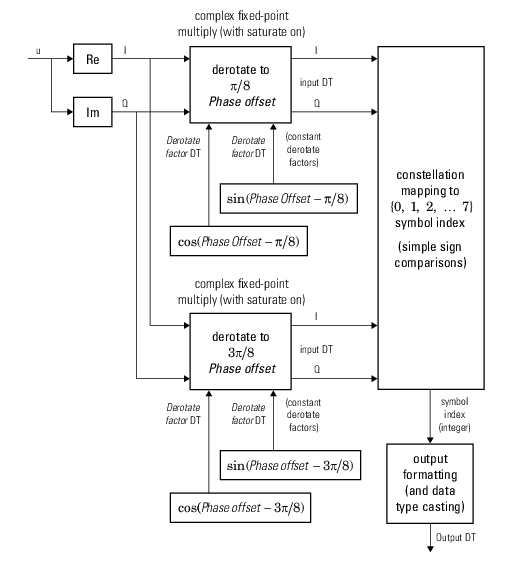
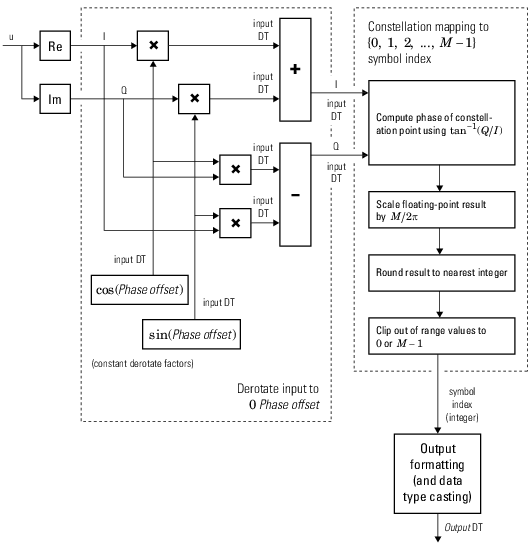
The comm.gpu.PSKDemodulator object demodulates a signal that was modulated using the M-ary phase shift keying (M-PSK) method implemented on a graphics processing unit (GPU). The input is a baseband representation of the modulated signal.

To demodulate a signal that was modulated using the M-PSK method:

Create the comm.gpu.PSKDemodulator object and set its properties.
Call the object with arguments, as if it were a function.

To learn more about how System objects work, see What Are System Objects?

Creation

Syntax

gpumpskdemod = comm.PSKDemodulator

gpumpskdemod = comm.PSKDemodulator(Name=Value)

gpumpskdemod = comm.PSKDemodulator(M,phase,Name=Value)

Description

gpumpskdemod = comm.PSKDemodulator creates a GPU-based demodulator System object™ that demodulates the input signal using the M-PSK method.

example

gpumpskdemod = comm.PSKDemodulator(Name=Value) sets properties using one or more name-value arguments. For example, comm.gpu.PSKDemodulator(DecisionMethod="Hard decision") specifies demodulation using the hard-decision method.

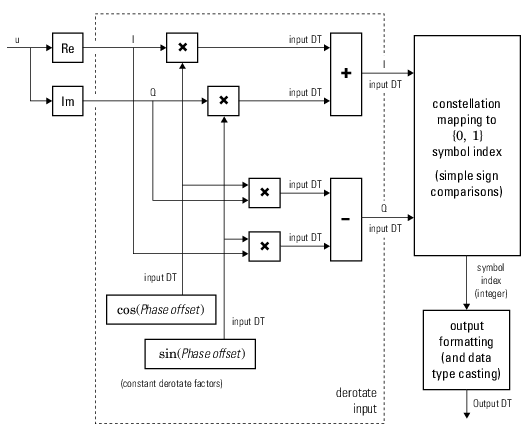
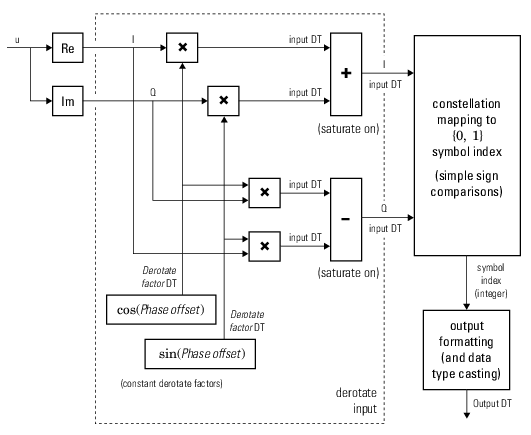
gpumpskdemod = comm.PSKDemodulator(M,phase,Name=Value) sets the ModulationOrder property to M, sets the PhaseOffset property to phase, and sets optional name-value arguments. Specify phase in radians.

example

Properties

expand all

Unless otherwise indicated, properties are nontunable, which means you cannot change their values after calling the object. Objects lock when you call them, and the release function unlocks them.

If a property is tunable, you can change its value at any time.

For more information on changing property values, see System Design in MATLAB Using System Objects.

`ModulationOrder` — Number of points in signal constellation
`8` (default) | positive integer

Number of points in signal constellation, specified as a positive integer.

Data Types: double

`PhaseOffset` — Phase of zeroth point in constellation
`pi/8` (default) | scalar

Phase of the zeroth point in the constellation in radians, specified as a scalar.

Example: PhaseOffset=0 aligns the QPSK signal constellation points on the axes {(1,0), (0,j), (-1,0), (0,-j)}.

Data Types: double

`BitOutput` — Option to output data as bits
`0` or `false` (default) | `1` or `true`

Option to output data as bits, specified as a logical 0 (false) or 1 (true).

Set this property to false to output data as integer values in the range [0, (ModulationOrder – 1)] with length equal to the input data vector.
Set this property to true to output data as a column vector of bit values with length equal to log2(ModulationOrder) times the number of demodulated symbols.

Data Types: logical

`SymbolMapping` — Symbol encoding mapping of constellation bits
`'Gray'` (default) | `'Binary'` | `'Custom'`

Symbol encoding mapping of the constellation bits, specified as 'Gray', 'Binary', or 'Custom'. Each integer or group of log2(ModulationOrder) bits corresponds to one symbol.

When you set this property to 'Gray', the object maps symbols to a Gray-encoded signal constellation.
When you set this property to 'Binary', the object maps symbols to a natural binary-encoded signal constellation. Specifically, the complex value e^{j(PhaseOffset
+
(2πm/ModulationOrder))}, where m is an integer in the range [0, (ModulationOrder – 1)].
When you set this property to 'Custom', the object maps symbols to the signal constellation defined in the CustomSymbolMapping property.

`CustomSymbolMapping` — Custom symbol encoding
`0:7` (default) | integer vector

Custom symbol encoding, specified as an integer vector with length equal to the value of ModulationOrder and unique values in the range [0, (ModulationOrder – 1)]. The first element of this vector corresponds to the constellation point at an angle of 0 + PhaseOffset, with subsequent elements running counterclockwise. The last element corresponds to the constellation point at an angle of –2π/ModulationOrder + PhaseOffset.

Dependencies

To enable this property, set the SymbolMapping property to 'Custom'.

Data Types: double

`DecisionMethod` — Demodulation decision method
`'Hard decision'` (default) | `'Log-likelihood ratio'` | `'Approximate log-likelihood ratio'`

Demodulation decision method, specified as 'Hard decision', 'Log-likelihood ratio', or 'Approximate log-likelihood ratio'. When you set the BitOutput property to false, the object always performs hard-decision demodulation.

Dependencies

To enable this property, set the BitOutput property to true.

`VarianceSource` — Source of noise variance
`'Property'` (default) | `'Input port'`

Source of noise variance, specified as 'Property' or 'Input port'.

Dependencies

To enable this property, set the BitOutput property to true and the DecisionMethod property to 'Log-likelihood ratio' or 'Approximate log-likelihood ratio'.

`Variance` — Noise variance
`1` (default) | positive scalar

Noise variance, specified as a positive scalar.

Tips

The exact LLR algorithm computes exponentials using finite precision arithmetic. For computations involving very large positive or negative magnitudes, the exact LLR algorithm yields:

Inf or -Inf if the noise variance is a very large value
NaN if the noise variance and signal power are both very small values

The approximate LLR algorithm does not compute exponentials. You can avoid Inf, -Inf, and NaN results by using the approximate LLR algorithm.

Dependencies

To enable this property, set the BitOutput property to true, the DecisionMethod property to 'Log-likelihood ratio' or 'Approximate log-likelihood ratio', and the VarianceSource property to 'Property'.

Data Types: double

`OutputDataType` — Data type of output
`'Full precision'` (default)

This property is read-only.

Data type of the output, specified as 'Full precision'. The output data type matches the input data type.

Usage

Syntax

y = gpumpskdemod(x)

y = gpumpskdemod(x,var)

Description

y = gpumpskdemod(x) applies M-PSK demodulation to the input signal and returns the demodulated signal.

example

y = gpumpskdemod(x,var) uses soft decision demodulation and noise variance var. This syntax applies when you set the BitOutput property to true, the DecisionMethod property to 'Approximate log-likelihood ratio' or 'Log-likelihood ratio', and the VarianceSource property to 'Input port'.

Input Arguments

expand all

`x` — M-PSK-modulated signal
scalar | column vector

M-PSK-modulated signal, specified as a scalar or column vector.

To decrease data transfer latency, format the input signal as a gpuArray (Parallel Computing Toolbox) object. For more information, see Array Processing with GPU-Based System Objects.

Data Types: double | single

`var` — Noise variance
scalar

Noise variance, specified as a scalar.

Dependencies

To enable this argument, set the VarianceSource property to 'Input port', the BitOutput property to true, and the DecisionMethod property to 'Approximate log-likelihood ratio' or 'Log-likelihood ratio'.

Data Types: single | double

Output Arguments

expand all

`y` — Output signal
scalar | column vector

Output signal, returned as a scalar or column vector. To specify whether the object outputs values as integers or bits, use the BitOutput property. The output data type matches the input data type.

Object Functions

To use an object function, specify the System object as the first input argument. For example, to release system resources of a System object named obj, use this syntax:

release(obj)

expand all

Specific to `comm.gpu.PSKDemodulator`

constellation Calculate or plot ideal signal constellation

Common to All System Objects

`step`	Run System object algorithm
`release`	Release resources and allow changes to System object property values and input characteristics
`reset`	Reset internal states of System object

Examples

collapse all

GPU PSK Demodulator

Open Script

Create a GPU PSK modulator and demodulator pair.

gpuMod = comm.gpu.PSKModulator;
gpuDemod = comm.gpu.PSKDemodulator;

Generate random data symbols. Modulate the data.

txData = randi([0 7],1000,1);
txSig = gpuMod(txData);

Pass the signal through an AWGN channel.

rxSig = awgn(txSig,20);

Demodulate the received signal.

rxData = gpuDemod(rxSig);

Determine the number of symbol errors.

numSymErrors = symerr(txData,rxData)

numSymErrors =

     0

Pass Data to GPU-Based System Objects Using gpuarray Input

Open Live Script

In this example, you transmit 1/2 rate convolutionally encoded 16-PSK-modulated data through an AWGN channel, demodulate and decode the received data, and assess the error rate of the received data. For this implementation, you use the GPU-based Viterbi decoder System object™ to process multiple signal frames in a single call and then use gpuArray (Parallel Computing Toolbox) objects to pass data into and out of the GPU-based System objects.

Create GPU-based System objects for PSK modulation and demodulation, convolutional encoding, and Viterbi decoding. Create a System object for error rate calculation.

M = 16; % Modulation order
numframes = 100;

gpuconvenc = comm.gpu.ConvolutionalEncoder;
gpupskmod = comm.gpu.PSKModulator(M,pi/16,BitInput=true);
gpupskdemod = comm.gpu.PSKDemodulator(M,pi/16,BitOutput=true);
gpuvitdec = comm.gpu.ViterbiDecoder( ...
    InputFormat='Hard', ...
    TerminationMethod='Truncated', ...
    NumFrames=numframes);
errorrate = comm.ErrorRate(ComputationDelay=0,ReceiveDelay=0);

Due to the computational complexity of the Viterbi decoding algorithm, loading multiple frames of signal data on the GPU and processing them in one call can reduce overall simulation time. To enable this implementation, the GPU-based Viterbi decoder System object contains a NumFrames property. Instead of using an external for-loop to process individual frames of data, you use the NumFrames property to configure the GPU-based Viterbi decoder System object to process multiple data frames. Generate numframes of binary data frames. To efficiently manage the data frames for processing by the GPU-based System objects, represent the transmission data frames as a gpuArray object.

numsymbols = 50;
rate = 1/2; 
dataA = gpuArray.randi([0 1],rate*numsymbols*log2(M),numframes);

The error rate object does not support gpuArray objects or multichannel data, so you must retrieve the array from the GPU by using the gather (Parallel Computing Toolbox) function to compute the error rate on each frame of data in a for-loop. Perform the GPU-based encoding, modulation, AWGN, and demodulation inside a for-loop.

for ii = 1:numframes
    encodedData = gpuconvenc(dataA(:,ii));
    modsig = gpupskmod(encodedData);
    noisysig = awgn(modsig,30); % SNR = 30 dB. Signal power = 0 dBW
    demodsig(:,ii) = gpupskdemod(noisysig);
end

The GPU-based Viterbi decoder performs multiframe processing without a for-loop.

rxbits = gpuvitdec(demodsig(:));

errorStats = errorrate(gather(dataA(:)),gather(rxbits));
fprintf('BER = %f\nNumber of errors = %d\nTotal bits = %d', ...
    errorStats(1), errorStats(2), errorStats(3))

BER = 0.009900
Number of errors = 99
Total bits = 10000

More About

expand all

Hard-Decision BPSK Demodulation

The signal preprocessing required for BPSK demodulation depends on the configuration.

This figure shows the hard-decision BPSK demodulation signal diagram for the trivial phase offset (multiple of π/2) configuration.

This figure shows the hard-decision BPSK demodulation floating-point signal diagram for the nontrivial phase offset configuration.

This figure shows the hard-decision BPSK demodulation fixed-point signal diagram for the nontrivial phase offset configuration.

Hard-Decision QPSK Demodulation

The signal preprocessing required for QPSK demodulation depends on the configuration.

This figure shows the hard-decision QPSK demodulation signal diagram for the trivial phase offset (odd multiple of π/4) configuration.

This figure shows the hard-decision QPSK demodulation floating-point signal diagram for the nontrivial phase offset configuration.

This figure shows the hard-decision QPSK demodulation fixed-point signal diagram for the nontrivial phase offset configuration.

Hard-Decision Higher-Order PSK

The signal preprocessing required for higher order PSK demodulation depends on the configuration.

This figure shows the hard-decision 8-PSK demodulation signal diagram for the trivial phase offset (odd multiple of π/8) configuration.

This figure shows the hard-decision 8-PSK demodulation fixed-point signal diagram for trivial phase offset (odd multiple of π/8) configuration.

This figure shows the hard-decision M-PSK demodulation floating-point signal diagram for the nontrivial phase offset configuration.

For M > 8, to improve speed and implementation costs, no derotation arithmetic is performed for trivial case (specifically, when phase offset is 0, π/2, π, or 3π/2).

Also, for M > 8, only double and single input types are supported.

Array Processing with GPU-Based System Objects

A GPU-based System object accepts typical MATLAB^® arrays or gpuArray (Parallel Computing Toolbox) objects. The output signal data type matches the input signal data type.

When the input signal to the GPU-based System object is a gpuArray object, calculations take place entirely on the GPU, the data remains on the GPU, and the output signal is a gpuArray object. Passing gpuArray arguments minimizes data transfer latency by limiting the number of data transfers between the CPU and the GPU when your simulation runs. For more information, see Establish Arrays on a GPU (Parallel Computing Toolbox).
When the input signal is a MATLAB array, the GPU-based System object transfers the data between the CPU and the GPU for each object call. The output signal is a MATLAB array and data transfer latency occurs.

References

[1] Proakis, John G. Digital Communications. 4th ed. New York: McGraw Hill, 2001.

Extended Capabilities

GPU Arrays
Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.

This System object supports GPU array inputs. For more information, see Accelerate Simulation Using GPUs.

Version History

Introduced in R2012a

comm.gpu.PSKDemodulator

Description

Creation

Syntax

Description

Properties

ModulationOrder — Number of points in signal constellation 8 (default) | positive integer

PhaseOffset — Phase of zeroth point in constellation pi/8 (default) | scalar

BitOutput — Option to output data as bits 0 or false (default) | 1 or true

SymbolMapping — Symbol encoding mapping of constellation bits 'Gray' (default) | 'Binary' | 'Custom'

CustomSymbolMapping — Custom symbol encoding 0:7 (default) | integer vector

Dependencies

DecisionMethod — Demodulation decision method 'Hard decision' (default) | 'Log-likelihood ratio' | 'Approximate log-likelihood ratio'

Dependencies

VarianceSource — Source of noise variance 'Property' (default) | 'Input port'

Dependencies

Variance — Noise variance 1 (default) | positive scalar

Tips

Dependencies

OutputDataType — Data type of output 'Full precision' (default)

Usage

Syntax

Description

Input Arguments

x — M-PSK-modulated signal scalar | column vector

var — Noise variance scalar

Dependencies

Output Arguments

y — Output signal scalar | column vector

Object Functions

Specific to comm.gpu.PSKDemodulator

Common to All System Objects

Examples

GPU PSK Demodulator

Pass Data to GPU-Based System Objects Using gpuarray Input

More About

Hard-Decision BPSK Demodulation

Hard-Decision QPSK Demodulation

Hard-Decision Higher-Order PSK

Array Processing with GPU-Based System Objects

References

Extended Capabilities

GPU Arrays Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.

Version History

See Also

Functions

Objects

Blocks

Topics

`ModulationOrder` — Number of points in signal constellation
`8` (default) | positive integer

`PhaseOffset` — Phase of zeroth point in constellation
`pi/8` (default) | scalar

`BitOutput` — Option to output data as bits
`0` or `false` (default) | `1` or `true`

`SymbolMapping` — Symbol encoding mapping of constellation bits
`'Gray'` (default) | `'Binary'` | `'Custom'`

`CustomSymbolMapping` — Custom symbol encoding
`0:7` (default) | integer vector

`DecisionMethod` — Demodulation decision method
`'Hard decision'` (default) | `'Log-likelihood ratio'` | `'Approximate log-likelihood ratio'`

`VarianceSource` — Source of noise variance
`'Property'` (default) | `'Input port'`

`Variance` — Noise variance
`1` (default) | positive scalar

`OutputDataType` — Data type of output
`'Full precision'` (default)

`x` — M-PSK-modulated signal
scalar | column vector

`var` — Noise variance
scalar

`y` — Output signal
scalar | column vector

Specific to `comm.gpu.PSKDemodulator`

GPU Arrays
Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.