info
Characteristic information about fading channel object
Syntax
Description
Examples
Use the info object function to get information from a comm.RayleighChannel object.
Create a Rayleigh channel object with two paths and data to pass through the channel.
rayleighchan = comm.RayleighChannel( ... SampleRate=1000, ... PathDelays=[0 4e-3], ... AveragePathGains=[0 0])
rayleighchan =
comm.RayleighChannel with properties:
SampleRate: 1000
PathDelays: [0 0.0040]
AveragePathGains: [0 0]
NormalizePathGains: true
MaximumDopplerShift: 1.0000e-03
DopplerSpectrum: [1×1 struct]
ChannelFiltering: true
PathGainsOutputPort: false
Show all properties
data = randi([0 1],600,1);
Check the Rayleigh channel object information.
info(rayleighchan)
ans = struct with fields:
ChannelFilterCoefficients: [2×5 double]
ChannelFilterDelay: 0
NumSamplesProcessed: 0
Pass data through the channel and check the object information again to see that the information structure accounts for the number of samples processed.
rayleighchan(data); Sint = info(rayleighchan)
Sint = struct with fields:
ChannelFilterCoefficients: [2×5 double]
ChannelFilterDelay: 0
NumSamplesProcessed: 600
Breaking down the group delay per path, the specified PathDelays times SampleRate results in ([0 4e-3]*1000) = [0 4] sample path delays. Since the requested path delays are all integer-valued, the implemented channel filter adds no excess delay to the channel output, and the ChannelFilterDelay field reports 0 samples for the delay. As configured, the channel results in a constant group delay equal to (PathDelays*SampleRate + ChannelFilterDelay) = ([0 4e-3]*1000 + 0) = [0 4] samples per path. Use the grpdelay function to confirm the group delay for each path.
figure subplot(2,1,1) grpdelay(Sint.ChannelFilterCoefficients(1,:),1) title('Integer Path Delay: Group Delay for First Delay Path') subplot(2,1,2) grpdelay(Sint.ChannelFilterCoefficients(2,:),1) title('Integer Path Delay: Group Delay for Second Delay Path')

Release the object so you can update attributes. Change the second path delay to a noninteger value of 1.5e-3 seconds. Implementing a filter with a noninteger path delay introduces excess group delay. The info object function reports this excess delay in the ChannelFilterDelay field of the information structure. Recheck the object configuration and information.
release(rayleighchan) rayleighchan.PathDelays = [0 1.5e-3]
rayleighchan =
comm.RayleighChannel with properties:
SampleRate: 1000
PathDelays: [0 0.0015]
AveragePathGains: [0 0]
NormalizePathGains: true
MaximumDopplerShift: 1.0000e-03
DopplerSpectrum: [1×1 struct]
ChannelFiltering: true
PathGainsOutputPort: false
Show all properties
rayleighchan(data); Snonint = info(rayleighchan)
Snonint = struct with fields:
ChannelFilterCoefficients: [2×16 double]
ChannelFilterDelay: 6
NumSamplesProcessed: 600
Breaking down the group delay per path, the specified PathDelays times SampleRate results in ([0 1.5e-3]*1000) = [0 1.5] sample path delays. Since the requested path delays contain at least one noninteger value, the channel filter implementation results in excess group delay at the channel output and the ChannelFilterDelay field now reports 6 samples for the delay. As configured, the channel results in a constant group delay equal to (PathDelays*SampleRate + ChannelFilterDelay) = ([0 1.5e-3]*1000 + 6) = [6 7.5] samples per path. Use the grpdelay function to confirm the group delay for each path.
figure subplot(2,1,1) grpdelay(Snonint.ChannelFilterCoefficients(1,:),1) title('Noninteger Path Delay: Group Delay for First Delay Path') subplot(2,1,2) grpdelay(Snonint.ChannelFilterCoefficients(2,:),1) title('Noninteger Path Delay: Group Delay for Second Delay Path')

Use the info object function to get information from a comm.RicianChannel object.
Create a Rician channel object with two paths and data to pass through the channel.
ricianchan = comm.RicianChannel( ... SampleRate=500, ... PathDelays=[0 2e-3], ... AveragePathGains=[0 0])
ricianchan =
comm.RicianChannel with properties:
SampleRate: 500
PathDelays: [0 0.0020]
AveragePathGains: [0 0]
NormalizePathGains: true
KFactor: 3
DirectPathDopplerShift: 0
DirectPathInitialPhase: 0
MaximumDopplerShift: 1.0000e-03
DopplerSpectrum: [1×1 struct]
ChannelFiltering: true
PathGainsOutputPort: false
Show all properties
data = randi([0 1],600,1);
Check the Rician channel object information.
info(ricianchan)
ans = struct with fields:
ChannelFilterCoefficients: [2×2 double]
ChannelFilterDelay: 0
NumSamplesProcessed: 0
Pass data through the channel and check the object information again to see that the information structure accounts for the number of samples processed.
ricianchan(data); Sint = info(ricianchan)
Sint = struct with fields:
ChannelFilterCoefficients: [2×2 double]
ChannelFilterDelay: 0
NumSamplesProcessed: 600
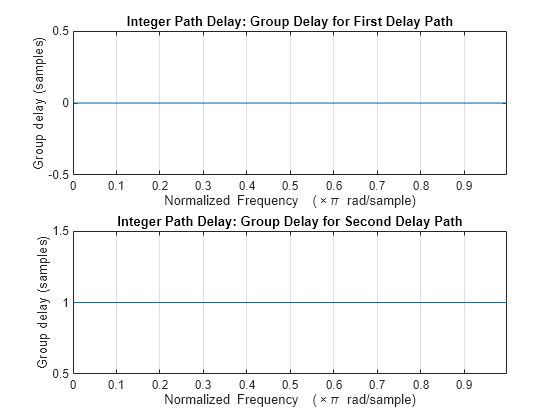
Breaking down the group delay per path, the specified PathDelays times SampleRate results in ([0 2e-3]*500) = [0 1] sample path delays. Since the requested path delays are all integer-valued, the implemented channel filter adds no excess delay to the channel output, and the ChannelFilterDelay field reports 0 samples for the delay. As configured, the channel results in a constant group delay equal to (PathDelays*SampleRate + ChannelFilterDelay) = ([0 2e-3]*500 + 0) = [0 1] samples per path. Use the grpdelay function to confirm the group delay for each path.
figure subplot(2,1,1) grpdelay(Sint.ChannelFilterCoefficients(1,:),1) title('Integer Path Delay: Group Delay for First Delay Path') subplot(2,1,2) grpdelay(Sint.ChannelFilterCoefficients(2,:),1) title('Integer Path Delay: Group Delay for Second Delay Path')
Release the object so you can update attributes. Change the second path delay to a noninteger value, such as 2.2e-3 seconds. Implementing a filter with a noninteger path delay introduces excess group delay. The info object function reports this excess delay in the ChannelFilterDelay field of the information structure. Recheck the object configuration and information.
release(ricianchan) ricianchan.PathDelays = [0 2.2e-3]; ricianchan(data); Snonint = info(ricianchan)
Snonint = struct with fields:
ChannelFilterCoefficients: [2×16 double]
ChannelFilterDelay: 6
NumSamplesProcessed: 600
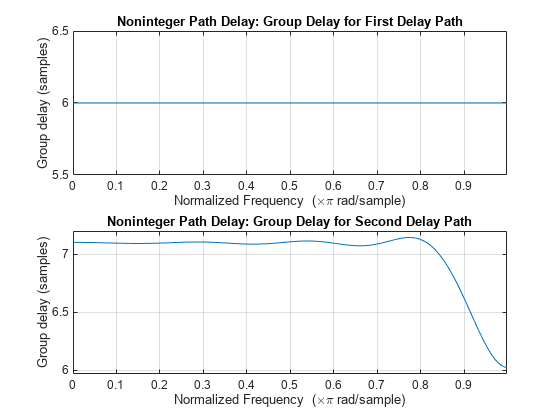
Breaking down the group delay per path, the specified PathDelays times SampleRate results in ([0 2.2e-3]*500) = [0 1.1] sample path delays. Since the requested path delays contain at least one noninteger value, the channel filter implementation results in excess group delay at the channel output and the ChannelFilterDelay field now reports 6 samples for the delay. For a Rician channel, the filter is not symmetric which can be observed by variation in the group delay for the second path. As configured, the channel results in a group delay centered around (PathDelays*SampleRate + ChannelFilterDelay) = ([0 2.2e-3]*500 + 6) = [6 7.1] samples per path. Use the grpdelay function to confirm the group delay for each path.
figure subplot(2,1,1) grpdelay(Snonint.ChannelFilterCoefficients(1,:),1) title('Noninteger Path Delay: Group Delay for First Delay Path') subplot(2,1,2) grpdelay(Snonint.ChannelFilterCoefficients(2,:),1) title('Noninteger Path Delay: Group Delay for Second Delay Path')
Use the info object function to get information from a comm.MIMOChannel object.
Create a MIMO channel object with one path and data to pass through the channel.
mimo = comm.MIMOChannel( ... SampleRate=1000, ... PathDelays=4e-3, ... AveragePathGains=0)
mimo =
comm.MIMOChannel with properties:
SampleRate: 1000
PathDelays: 0.0040
AveragePathGains: 0
NormalizePathGains: true
FadingDistribution: 'Rayleigh'
MaximumDopplerShift: 1.0000e-03
DopplerSpectrum: [1×1 struct]
SpatialCorrelationSpecification: 'Separate Tx Rx'
TransmitCorrelationMatrix: [2×2 double]
ReceiveCorrelationMatrix: [2×2 double]
AntennaSelection: 'Off'
NormalizeChannelOutputs: true
ChannelFiltering: true
PathGainsOutputPort: false
Show all properties
data = randi([0 1],600,2);
Check the MIMO channel object information.
info(mimo)
ans = struct with fields:
ChannelFilterCoefficients: [0 0 0 0 1]
ChannelFilterDelay: 0
NumSamplesProcessed: 0
Pass data through the channel and check the object information again to see that the information structure accounts for the number of samples processed.
mimo(data); Sint = info(mimo)
Sint = struct with fields:
ChannelFilterCoefficients: [0 0 0 0 1]
ChannelFilterDelay: 0
NumSamplesProcessed: 600
Breaking down the group delay, the specified PathDelays times SampleRate results in (4e-3*1000) = 4 sample path delay. Since the requested path delay is integer-valued, the implemented channel filter adds no excess delay to the channel output, and the ChannelFilterDelay field reports 0 samples for the delay. As configured, the channel results in a constant group delay equal to (PathDelays*SampleRate + ChannelFilterDelay) = (4e-3*1000 + 0) = 4 samples. Use the grpdelay function to confirm the group delay for the integer path delay.
grpdelay(Sint.ChannelFilterCoefficients,1)
title('Integer Path Delay: Group Delay')
Release the object so you can update attributes. Change the path delay to a noninteger value, such as 2.5e-3 seconds. Implementing a filter with a noninteger path delay introduces excess group delay. The info object function reports this excess delay in the ChannelFilterDelay field of the information structure. Recheck the object configuration and information.
release(mimo) mimo.PathDelays = 2.5e-3
mimo =
comm.MIMOChannel with properties:
SampleRate: 1000
PathDelays: 0.0025
AveragePathGains: 0
NormalizePathGains: true
FadingDistribution: 'Rayleigh'
MaximumDopplerShift: 1.0000e-03
DopplerSpectrum: [1×1 struct]
SpatialCorrelationSpecification: 'Separate Tx Rx'
TransmitCorrelationMatrix: [2×2 double]
ReceiveCorrelationMatrix: [2×2 double]
AntennaSelection: 'Off'
NormalizeChannelOutputs: true
ChannelFiltering: true
PathGainsOutputPort: false
Show all properties
Snonint = info(mimo)
Snonint = struct with fields:
ChannelFilterCoefficients: [-0.0326 0.0403 -0.0504 0.0646 -0.0861 0.1238 -0.2101 0.6359 0.6359 -0.2101 0.1238 -0.0861 0.0646 -0.0504 0.0403 -0.0326]
ChannelFilterDelay: 5
NumSamplesProcessed: 0
Breaking down the group delay, the specified PathDelays times SampleRate results in (2.5e-3*1000) = 2.5 sample path delay. Since the requested path delay contains a noninteger value, the channel filter implementation results in excess group delay at the channel output and the ChannelFilterDelay field now reports 5 samples for the delay. As configured, the channel results in a constant group delay equal to (PathDelays*SampleRate + ChannelFilterDelay) = (2.5e-3*1000 + 5) = 7.5 samples. Use the grpdelay function to compare the group delay for the integer and noninteger path delay.
figure subplot(2,1,1) grpdelay(Sint.ChannelFilterCoefficients,1) title('Integer Path Delay: Group Delay') subplot(2,1,2) grpdelay(Snonint.ChannelFilterCoefficients,1) title('Noninteger Path Delay: Group Delay')

Show that the channel state is maintained for discontinuous transmissions by using MIMO channel System objects configured to use the sum-of-sinusoids fading technique. Observe discontinuous channel response segments overlaid on a continuous channel response.
Set the channel properties.
fs = 1000; % Sample rate (Hz) pathDelays = [0 2.5e-3]; % Path delays (s) pathPower = [0 -6]; % Path power (dB) fD = 5; % Maximum Doppler shift (Hz) ns = 1000; % Number of samples nsdel = 100; % Number of samples for delayed paths
Define a continuous time span and three discontinuous time segments over which to plot and view the channel response. View a 1000-sample continuous channel response starting at time 0 and three 100-sample channel responses starting at times 0.1, 0.4, and 0.7 seconds, respectively.
to0 = 0.0; to1 = 0.1; to2 = 0.4; to3 = 0.7; t0 = (to0:ns-1)/fs; % Transmission 0 t1 = to1+(0:nsdel-1)/fs; % Transmission 1 t2 = to2+(0:nsdel-1)/fs; % Transmission 2 t3 = to3+(0:nsdel-1)/fs; % Transmission 3
Create a flat-fading 2-by-2 MIMO channel System object, disabling channel filtering and specifying a 1000 Hz sampling rate, the sum-of-sinusoids fading technique, and the number of samples to view. Specify a seed value so that results can be repeated. Use the default InitialTime property setting so that the fading channel is simulated from time 0.
mimoChan1 = comm.MIMOChannel('SampleRate',fs, ... 'MaximumDopplerShift',fD, ... 'RandomStream','mt19937ar with seed', ... 'Seed',17, ... 'FadingTechnique','Sum of sinusoids', ... 'ChannelFiltering',false, ... 'NumSamples',ns);
Create a clone of the MIMO channel System object. Change the number of samples for the delayed paths and the source for the initial time so that you can specify the fading channel offset time as an input argument when calling the System object.
mimoChan2 = clone(mimoChan1);
mimoChan2.InitialTimeSource = 'Input port';
mimoChan2.NumSamples = nsdel;Save the path gain output for the continuous channel response by using the mimoChan1 object and for the discontinuous delayed channel responses by using the mimoChan2 object with initial time offsets provided as input arguments.
pg0 = mimoChan1(); pg1 = mimoChan2(to1); pg2 = mimoChan2(to2); pg3 = mimoChan2(to3);
Compare the number of samples processed by the two channels by using the info method. The results show that mimoChan1 processed 1000 samples and that mimoChan2 processed only 300 samples.
G = info(mimoChan1); H = info(mimoChan2); [G.NumSamplesProcessed H.NumSamplesProcessed]
ans = 1×2
1000 300
Convert the path gains into decibels for the path corresponding to the first transmit and first receive antenna.
pathGain0 = 20*log10(abs(pg0(:,1,1,1))); pathGain1 = 20*log10(abs(pg1(:,1,1,1))); pathGain2 = 20*log10(abs(pg2(:,1,1,1))); pathGain3 = 20*log10(abs(pg3(:,1,1,1)));
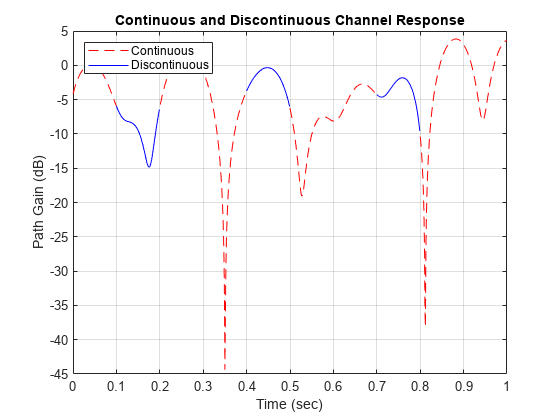
Plot the path gains for the continuous and discontinuous cases. The results show that the gains for the three segments match the gain for the continuous case. The alignment of the two shows that the sum-of-sinusoids technique is ideally suited to the simulation of packetized data because the channel characteristics are maintained even when data is not transmitted.
plot(t0,pathGain0,'r--') hold on plot(t1,pathGain1,'b') plot(t2,pathGain2,'b') plot(t3,pathGain3,'b') grid title('Continuous and Discontinuous Channel Response') xlabel('Time (sec)') ylabel('Path Gain (dB)') legend('Continuous','Discontinuous','location','nw')
Input Arguments
System object to get information from, specified as a comm.MIMOChannel, comm.RayleighChannel, or
comm.RicianChannel
System object.
Output Arguments
Structure containing these fields with information about the System object.
Excess filter delay in samples, returned as a positive integer.
If you configure the
PathDelaysproperty of your channel object with all integer-valued delays, the implemented channel filter adds no excess delay to the channel output. In this case, theChannelFilterDelayfield reports0for the excess path delay.If you configure the
PathDelaysproperty of your channel object with any noninteger-valued delays, the implemented channel filter may add excess delay to the channel output. In this case, theChannelFilterDelayfield may report a nonzero value for the excess path delay.
Channel filter coefficients, returned as a matrix. The time varying path gains are applied as gains to this non-varying filter to produce the channel output over time
Number of samples processed by the channel object since the last reset, returned as a positive integer.
Last frame ending time in seconds, returned as a positive scalar. Use this value to confirm the simulation time.
Dependencies
This property applies when the
FadingTechnique property is
'Sum of sinusoids' and the
InitialTimeSource property is
'Input port'.
Version History
Introduced in R2012a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
选择网站
选择网站以获取翻译的可用内容,以及查看当地活动和优惠。根据您的位置,我们建议您选择:。
您也可以从以下列表中选择网站:
如何获得最佳网站性能
选择中国网站(中文或英文)以获得最佳网站性能。其他 MathWorks 国家/地区网站并未针对您所在位置的访问进行优化。
美洲
- América Latina (Español)
- Canada (English)
- United States (English)
欧洲
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)