M-APSK Demodulator Baseband
M-ary amplitude phase shift keying (APSK) demodulation
Libraries:
Communications Toolbox /
Modulation /
Digital Baseband Modulation /
APM
Description
The M-APSK Demodulator Baseband block demodulates a baseband representation of an M-ary amplitude phase shift keying (APSK) modulated signal. M is the Modulation Order for M-APSK. For a description of M-APSK demodulation, see APSK Hard Demodulation and APSK Soft Demodulation.
Note
M-APSK Demodulator Baseband specifically applies to multiple ring PSK constellations. For a single ring PSK constellation, use M-PSK Demodulator Baseband.
This icon shows the block with all ports enabled: ![]()
Examples
Apply 16-APSK modulation to a signal of random data. Pass the modulated signal through an AWGN channel. Demodulate the noisy 16-APSK signal. The example reports bit error rate (BER) and symbol error rate (SER) at two SNR settings.
The slex_16apsk_mod model passes a 16-APSK modulated signal through an AWGN channel, demodulates the signal and then computes the error rate statistics. The upper workflow computes the BER and the lower workflow computes the SER. Some block parameters get set by using workspace variables initialized in the PreLoadFcn callback function loads simulation variables into the workspace. For more information, see Model Callbacks (Simulink).
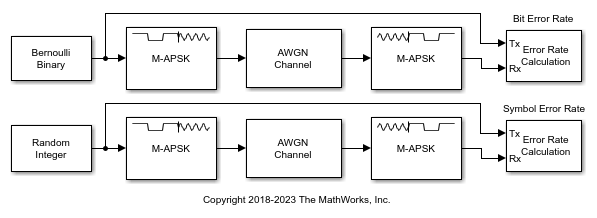
Run the model with the AWGN channel blocks set to EbN0 = 6 dB and display the computed BER and SER. The AWGN Channel block in the lower workflow converts the EbN0 setting to an EsN0 setting. The results are saved to the workspace variables BERVec and SERVec in 1-by-3 row vectors. The first element contains the error rate.
With EbN0 set to 6.00 dB, BER: 0.070 With EsN0 set to 12.02 dB, SER: 0.160
Change the EbN0 of the AWGN channel block to 10 dB. Run the model, display the computed BER and SER, and observe the decrease in error rate.
With EbN0 set to 10.00 dB, BER: 0.016 With EsN0 set to 16.02 dB, SER: 0.051
Ports
Input
APSK modulated signal, specified as a scalar, vector, or matrix. When
this input is a matrix, each column is treated as an independent
channel. This port is unnamed until the Var port is
enabled.
Data Types: double | single
Complex Number Support: Yes
Noise variance, specified as a positive scalar or vector of positive values. When the noise variance or signal power result in computations involving extreme positive or negative magnitudes, see APSK Soft Demodulation for demodulation decision type considerations.
Dependencies
To enable this port, set Noise variance source to Input
port.
Data Types: double | single
Output
Demodulated signal, returned as a scalar, vector, or matrix. The data type and dimensions of the demodulated signal depend on the values specified by the Output type and Decision type parameters. This port is unnamed on the block.
| Output type | Decision type | Demodulated Signal Description | Dimensions of Demodulated Signal |
|---|---|---|---|
Integer | — | Demodulated integer values in the range [0, (M – 1)] | The output signal has the same dimensions as the input signal. |
Bit | Hard decision | Demodulated bits | The number of rows in the output signal is log2(M) times the number of rows in the input signal. Each demodulated symbol is mapped to a group of log2(M) elements in a column, where the first element represents the MSB and the last element represents the LSB. |
Log-likelihood
ratio | Log-likelihood ratio value for each bit | ||
Approximate log-likelihood
ratio | Approximate log-likelihood ratio value for each bit | ||
M is the Modulation Order for M-APSK. | |||
Use Output data type to specify the output data type.
Data Types: single | double
Parameters
To edit block parameters interactively, use the Property Inspector. From the Simulink® Toolstrip, on the Simulation tab, in the Prepare gallery, select Property Inspector.
Constellation points per PSK ring, specified as a vector with more than one element. Each vector element indicates the number of constellation points in its corresponding PSK ring. The first element corresponds to the innermost circle, and so on until the last element, which corresponds to the outermost circle. The sum of the elements in Constellation points per circle determines the modulation order. Element values must be multiples of four, and the modulation order must be a power of two.
Example: [4,12,16] specifies a three PSK ring
constellation with a modulation order of 32.
Radius per PSK ring, specified as a vector with the same length as Constellation points per circle. Each vector element indicates the radius of its corresponding PSK ring. The first element corresponds to the innermost circle, and so on until the last element, which corresponds to the outermost circle. These element values must be positive values arranged in increasing order.
Example: [0.5,1,2] defines radii for three constellation
PSK rings. The inner ring has a radius of 0.5, the second ring has a radius
of 1.0, and the outer ring has a radius of 2.0.
Phase offset per PSK ring in radians, specified as a scalar or vector with the same length as Constellation points per circle. Each vector element indicates the phase offset of its corresponding PSK ring. The first element corresponds to the innermost circle, and so on until the last element, which corresponds to the outermost circle. The Phase offset of each circle (rad) can be a scalar only if all the elements of Constellation points per circle are the same value.
Example: [pi/4,pi/12,pi/16] defines phase offsets for
three constellation PSK rings. The inner ring has a phase offset of π/4, the
second ring has a phase offset of π/12, and the outer ring has a phase
offset of π/16.
Symbol mapping, specified as one of the following:
Contourwise-gray— Uses Gray mapping along the contour in the phase dimension for each PSK ring.Gray— Uses Gray mapping along the contour in both the amplitude and phase dimensions. For Gray symbol mapping, all elements in Constellation points per circle must be equal, and all elements in Phase offset of each circle (rad) must be equal. For a description of the Gray mapping used, see [2].User-defined— See Custom symbol mapping.
The default symbol mapping depends on the
Constellation points per circle and Phase
offset of each circle (rad) parameters. When all elements in
Constellation points per circle are equal, and all
elements in Phase offset of each circle (rad) are
equal, the default is Gray. For all other cases,
the default is Contourwise-gray.
Custom symbol mapping, specified as an integer vector. This vector must consist of M unique elements with values in the range [0, (M – 1)], where M is the Modulation Order for M-APSK. The first element in Custom symbol mapping corresponds to the constellation point in the first quadrant of the innermost circle, with subsequent elements positioned counterclockwise around the PSK rings.
Example: The default value,
[0,4,12,8,1,3,2,6,7,5,13,15,14,10,11,9], specifies
contourwise-gray symbol mapping. The distribution of constellation points is
nonuniform on all contours.
Dependencies
To enable this parameter, set Symbol
mapping to
User-defined.
Output type, specified as Integer or
Bit.
Demodulation decision type, specified as Hard
decision, Log-likelihood ratio,
or Approximate log-likelihood ratio. See APSK Soft Demodulation for
algorithm selection considerations.
Dependencies
This parameter applies only when Output
type is set to Bit.
Noise variance source, specified as:
Property— The noise variance is set using the Noise variance parameter.Input port— The noise variance is set using the Var input port.
Dependencies
This parameter applies only when Decision type is set to either
Log-likelihood ratio or
Approximate log-likelihood ratio.
Noise variance, specified as a positive scalar or vector of positive values.
When specified as a scalar, that value is used on all elements in the input signal.
When specified as a vector, the vector length must be equal to the number of columns in the input signal. Each noise variance vector element is applied to its corresponding column in the input signal.
When the noise variance or signal power result in computations involving extreme positive or negative magnitudes, see APSK Soft Demodulation for Decision type specification considerations.
Dependencies
This parameter applies only when Noise
variance source is set to
Property and Decision type is set to either
Log-likelihood ratio or
Approximate log-likelihood ratio.
Output data type, specified as one of the acceptable values from this table. Acceptable Output data type values depend on the Output type and Decision type parameter values.
| Output type | Decision type | Output data type Options |
|---|---|---|
Integer | Not applicable | double,
single,
int8,
uint8,
int16,
uint16,
int32, or
uint32 |
Bit | Hard decision | double,
single,
int8,
uint8,
int16,
uint16,
int32,
uint32, or
logical |
Log-likelihood ratio or
Approximate log-likelihood
ratio | The output signal is the same data type as the input signal. |
Dependencies
This parameter applies only when Output
type is set to Integer or
when Output
type is set to Bit and
Decision type is set to Hard
decision.
Type of simulation to run, specified as Interpreted
execution or Code generation.
Interpreted execution— Simulate the model by using the MATLAB® interpreter. This option requires less startup time, but the speed of subsequent simulations is slower than with theCode generationoption. In this mode, you can debug the source code of the block.Code generation— Simulate the model by using generated C code. The first time you run a simulation, Simulink generates C code for the block. The model reuses the C code for subsequent simulations unless the model changes. This option requires additional startup time, but the speed of the subsequent simulations is faster than with theInterpreted executionoption.
For more information, see Interpreted Execution vs. Code Generation (Simulink).
Block Characteristics
Data Types |
|
Multidimensional Signals |
|
Variable-Size Signals |
|
More About
The modulation order, M, for M-APSK equals the sum of the vector elements in the Constellation points per circle parameter and is the total number of points in the signal constellation. Element values in Constellation points per circle must be multiples of four, and M must be a power of two.
The hard demodulation algorithm applies amplitude phase decoding, as described in [1].
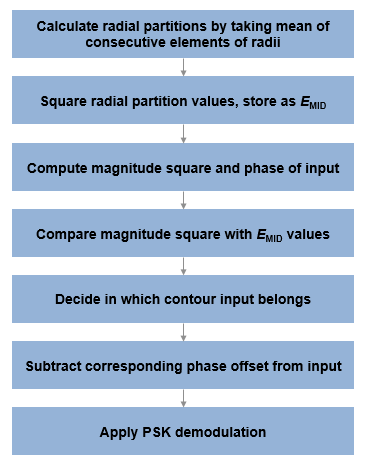
For soft demodulation, two soft-decision log-likelihood ratio (LLR) algorithms are available: exact LLR and approximate LLR. The exact LLR algorithm is more accurate but has slower execution speed than the approximate LLR algorithm. For further description of these algorithms, see the Hard- vs. Soft-Decision Demodulation topic.
Note
The exact LLR algorithm computes exponentials using finite precision arithmetic. For computations involving very large positive or negative magnitudes, the exact LLR algorithm yields:
Infor-Infif the noise variance is a very large valueNaNif the noise variance and signal power are both very small values
The approximate LLR algorithm does not compute exponentials. You can avoid
Inf, -Inf, and NaN results by using
the approximate LLR algorithm.
Tips
For faster execution of the M-APSK Demodulator Baseband block, set the Simulate using parameter to:
Code generationwhen using hard decision demodulation.Interpreted executionwhen using soft decision demodulation.
References
[1] Sebesta, J. “Efficient Method for APSK Demodulation.” Selected Topics on Applied Mathematics, Circuits, Systems, and Signals (P. Pardalos, N. Mastorakis, V. Mladenov, and Z. Bojkovic, eds.). Vouliagmeni, Athens, Greece: WSEAS Press, 2009.
[2] Liu, Z., Q. Xie, K. Peng, and Z. Yang. "APSK Constellation with Gray Mapping." IEEE Communications Letters. Vol. 15, Number 12, December 2011, pp. 1271–1273.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.
Version History
Introduced in R2018b
See Also
Blocks
Functions
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
选择网站
选择网站以获取翻译的可用内容,以及查看当地活动和优惠。根据您的位置,我们建议您选择:。
您也可以从以下列表中选择网站:
如何获得最佳网站性能
选择中国网站(中文或英文)以获得最佳网站性能。其他 MathWorks 国家/地区网站并未针对您所在位置的访问进行优化。
美洲
- América Latina (Español)
- Canada (English)
- United States (English)
欧洲
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)