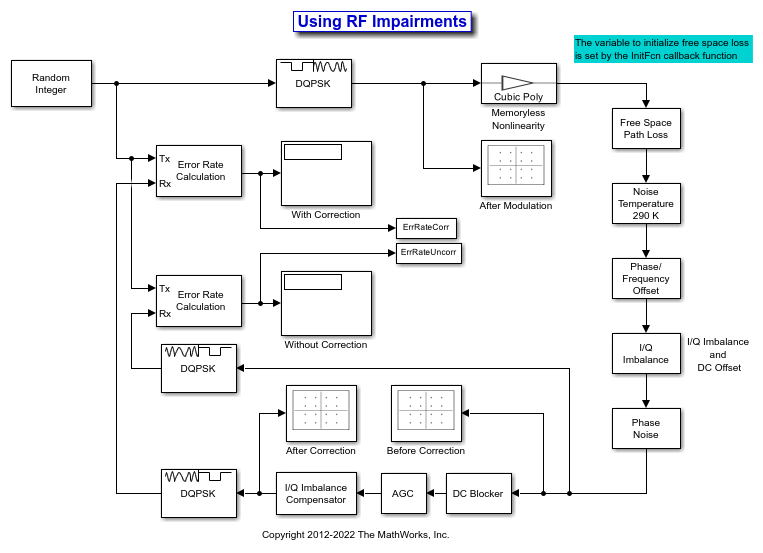
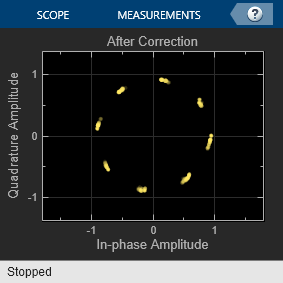
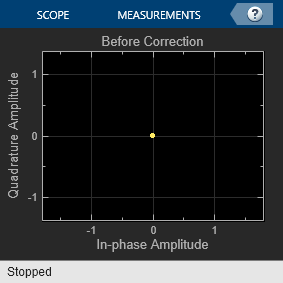
Memoryless Nonlinearity
Apply amplifier models to complex baseband signal
Libraries:
Communications Toolbox /
RF Impairments and Components
Description
The Memoryless Nonlinearity block applies amplifier models to a complex baseband signal. Use this block to model memoryless nonlinear impairments caused by signal amplification in the radio frequency (RF) transmitter or receiver. For more information, see Amplifier Model Methods.
Examples
Ports
Input
Output
Parameters
Block Characteristics
Data Types |
|
Multidimensional Signals |
|
Variable-Size Signals |
|
More About
Tips
To visualize the power characteristics of your model, set the parameters listed in the table and click the Plot power characteristics button.
Model Parameters and Example Values Power Characteristics Plot Cubic Polynomial Main tab:
Linear power gain (dB):
7Type of Non-linearity:
IIP3IIP3 (dBm):
33Simulate using:
Code generation

AM/AM - AM/PM Main tab:
Lookup table (Pin(dBm), Pout(dBm), deg):
[-25, 5, -1; -10, 20, -2; 0, 27, 5; 5, 28, 12]Simulate using:
Code generation

Note
To determine appropriate Pout (dBm) and
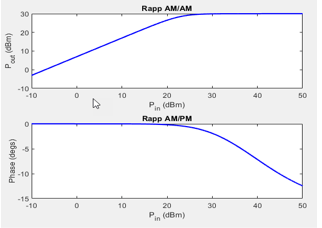
degvalues for any Pin (dBm) values below the value specified in the first row of the Lookup table (Pin(dBm), Pout(dBm), deg) parameter, the block applies the same power gain anddegas the first row, to maintain linearity and phase continuity. For any Pin (dBm) higher than the value in the last row of the Lookup table (Pin(dBm), Pout(dBm), deg) parameter, the block uses linear extrapolation from last two rows of the Lookup table (Pin(dBm), Pout(dBm), deg).Modified Rapp Main tab:
Linear power gain (dB):
7Output saturation level (V):
1Magnitude smoothness factor:
2Phase gain (rad):
-.45Phase saturation:
0.88Phase smoothness factor:
3.43Simulate using:
Code generation
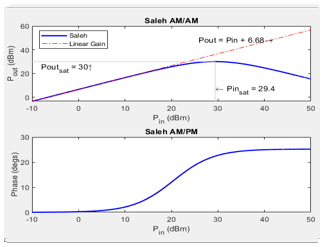
Saleh Main tab:
Input scaling (dB):
0AM/AM parameters [alpha beta]:
[ 2.1587, 1.1517 ]AM/PM parameters [alpha beta]:
[ 4.0033, 9.1040 ]Output scaling (dB):
0Simulate using:
Interpreted execution
References
[1] Saleh, A.A.M. “Frequency-Independent and Frequency-Dependent Nonlinear Models of TWT Amplifiers.” IEEE® Transactions on Communications 29, no. 11 (November 1981): 1715–20. https://doi.org/10.1109/TCOM.1981.1094911.
[2] Ghorbani, A., and M. Sheikhan. "The Effect of Solid State Power Amplifiers (SSPAs) Nonlinearities on MPSK and M-QAM Signal Transmission." In 1991 Sixth International Conference on Digital Processing of Signals in Communications (1991): 193–97.
[3] Rapp, Ch. "Effects of HPA-Nonlinearity on a 4-DPSK/OFDM-Signal for a Digital Sound Broadcasting System." In Proceedings Second European Conf. on Sat. Comm. (ESA SP-332), 179–84. Liege, Belgium, 1991. https://elib.dlr.de/33776/.
[4] Kundert, Ken."Accurate and Rapid Measurement of IP2 and IP3," The Designer Guide Community, May 22, 2002.