ofdmEqualize

Obtain the channel response for a beamformed OFDM signal with ${\mathit{N}}_{\mathrm{S}}$ parallel data streams filtered through an ${\mathit{N}}_{\mathrm{T}}$-by-${\mathit{N}}_{\mathrm{R}}$ MIMO channel. Use the channel response to apply OFDM equalization to the received OFDM-demodulated signal.

Define simulation variables.

rng(1);
numStreams = 2;  % Number of parallel data streams (Ns)
numTx = 4;       % Number of transmit antennas (Nt)
numRx = 3;       % Number of receive antennas (Nr)
bps = 6;         % Bits per QAM symbol (and OFDM data subcarrier)
nfft = 256;      % FFT length
cpLen = 16;      % Cyclic prefix length
numOFDMSym = 10; % Number of OFDM symbols
SNRdB = 40;      % Signal-to-noise ratio

Check that the number of data streams is no greater than either the number of transmit antennas or the number of receive antennas.

if numStreams > min(numTx,numRx)
    error('numStreams must be equal to or less than numTx and numRx.');
end

Configure OFDM subcarriers.

ofdmNullIdx = ...   % Guard bands and DC subcarrier
    [1:9 (nfft/2+1) (nfft-8+1:nfft)]'; 
numDataSC = ...     % Number of data subcarriers
    nfft-length(ofdmNullIdx);

Generate an array of data symbols consisting of ${\mathit{N}}_{\mathrm{S}}$ parallel data streams, QAM-modulate the symbols, and then OFDM-modulate the QAM-modulated symbols.

dataBits = randi([0,1],[numDataSC*bps numOFDMSym numStreams]);
M = 2^bps; % Modulation order
qamTx = qammod(dataBits,M, ...
    InputType="bit", ...
    UnitAveragePower=true);
ofdmOut = ofdmmod(qamTx,nfft,cpLen,ofdmNullIdx);

Beamforming expands the dimensionality of the transmit signal to improve link performance over multipath channels. The data streams are fed through a beamformer that focuses the transmit energy over an ${\mathit{N}}_{\mathrm{T}}$-by-1 transmit antenna array where the number of antennas ${\mathit{N}}_{\mathrm{T}}\ge {\mathit{N}}_{\mathrm{S}}$.

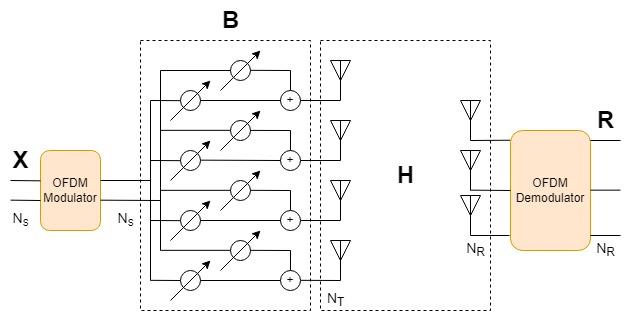
Form a beamformer matrix from steering vectors acting on each stream.

% Beamform the transmitted signal
fc = 1e9;
lambda = physconst('LightSpeed')/fc;
beamAngles = 15;
antIdx = (0:numTx-1);
antDelay = 2*pi*sin(2*pi*beamAngles*(0:numStreams-1).'/360)/lambda;
B = exp(1i*antIdx.*antDelay);  % Ns x Nt beamformer matrix
txOut = ofdmOut * B;

Filter the OFDM-modulated signal through a MIMO channel to get the channel coefficients.

mimoChannel = comm.MIMOChannel( ...
    SampleRate=1e6, ...
    PathDelays=[0 3e-6 5e-6], ...
    AveragePathGains=[0 0.5 0.2], ...
    MaximumDopplerShift=0, ...
    SpatialCorrelationSpecification="None", ...
    NumTransmitAntennas=numTx, ...
    NumReceiveAntennas=numRx, ...
    PathGainsOutputPort=true);
[channelOut,pathGains] = mimoChannel(txOut);

In a practical system, the channel must be sounded to estimate the channel response. Instead of sounding, the ofdmChannelResponse function computes the exact channel response using the path gains and path filters that are available after you pass data through the MIMO channel System object. Use channel path gains returned by the MIMO channel object, and the path filters and timing offset returned by the info object function, to obtain the OFDM channel response. If ${\mathit{N}}_{\mathrm{T}}<{\mathit{N}}_{\mathrm{R}}$, the channel forms an over-determined system (there are more receive antennas than necessary to adequately decode the transmitted signals). Call ofdmChannelResponse with the pathGains from the MIMO channel function to get the channel response.

mimoChannelInfo = info(mimoChannel);
pathFilters = mimoChannelInfo.ChannelFilterCoefficients;
toffset = mimoChannelInfo.ChannelFilterDelay;
h = ofdmChannelResponse(pathGains,pathFilters,nfft,cpLen, ...
    setdiff(1:nfft,ofdmNullIdx),toffset); % Nsc x Nsym x Nt x Nr

[rxIn,nVar] = awgn(channelOut,SNRdB,"measured");

Before demodulating the OFDM signal, account for the timing offset and symbol offset, remove the initial samples, and then pad with zeros to keep the signal length unchanged.

zeropadding = zeros(toffset,numRx);
ofdmDemodIn = [rxIn(toffset+1:end,:); zeropadding];
symOffset = cpLen/2;

OFDM-demodulate and equalize the received signal.

rxSym = ofdmdemod(ofdmDemodIn,nfft,cpLen,symOffset,ofdmNullIdx);

The effects of beamforming and the MIMO channel affect the received data streams. The effective channel (${\mathit{H}}_{\mathrm{eff}}$) is an ${\mathit{N}}_{\mathrm{S}}$-by-${\mathit{N}}_{\mathrm{R}}$ matrix defined as the product of the transmit beamformer and the MIMO channel coefficients.

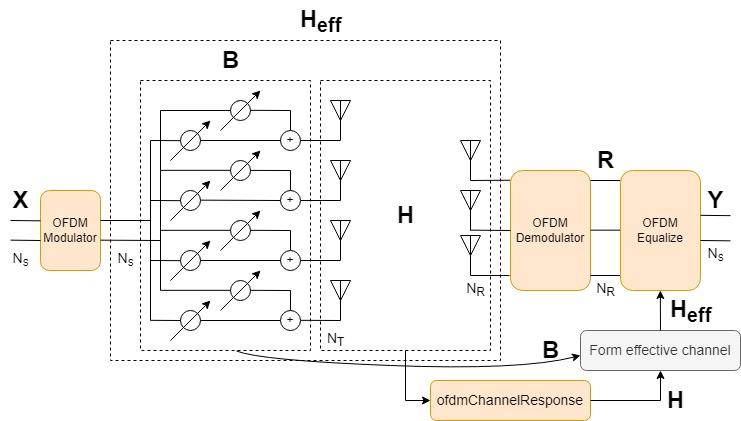
To use the OFDM channel response when equalizing the OFDM-demodulated signal, you must reshape the ${\mathit{N}}_{\mathit{SC}}$-by-${\mathit{N}}_{\mathrm{OFDMsym}}$-by-${\mathit{N}}_{\mathrm{T}}$-by-${\mathit{N}}_{\mathrm{R}}$ array to an ${\mathit{N}}_{\mathrm{QAMsym}}$-by-${\mathit{N}}_{\mathrm{T}}$-by-${\mathit{N}}_{\mathrm{R}}$ array. Form the effective channel using the beamformer matrix B and the reshaped channel coefficients h. Equalize the received OFDM signal using the calculated effective channel, the noise variance, and the MMSE algorithm.

hReshaped = reshape(h,[],numTx,numRx);

hEff = zeros(numDataSC*numOFDMSym,numStreams,numRx);
for k = 1:numOFDMSym*numDataSC
    hEff(k,:,:) = B * squeeze(hReshaped(k,:,:));
end

eqSym = ofdmEqualize(rxSym,hEff,nVar);

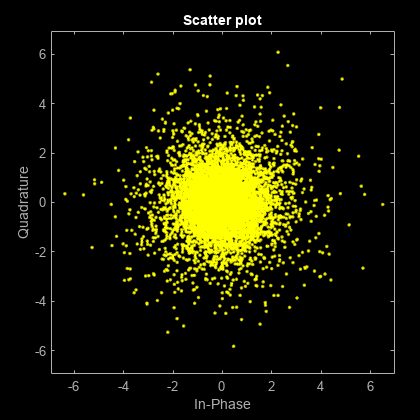
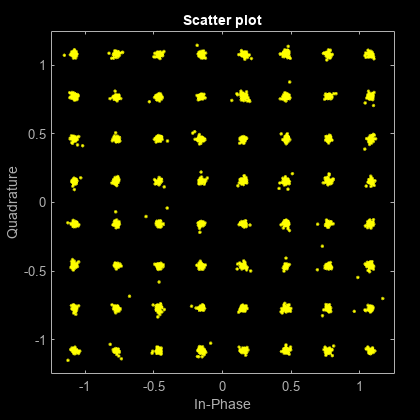
Show the received OFDM-demodulated symbols (rxSym) and the equalized OFDM-demodulated symbols (eqSym). The constellation of the OFDM-demodulated symbols before equalization does not resemble the QAM constellation. After equalization, the constellation points lay near the reference constellation.

figure(1);
scatterplot(rxSym(:));

figure(2);
scatterplot(eqSym(:));

Initialize variables for simulation of a MIMO system and a 120-resource-element subset of the OFDM subcarrier-symbol grid.

Nre = 120;  % Number of resource elements
Ns = 4;     % Number of data streams
Nr = 8;     % Number of receive antennas
nvar = 0.1; % Noise variance

Create random signals for a 2-D symbol array and a channel estimate.

rxsym2d = complex(randn(Nre,Nr),randn(Nre,Nr));
Hest = complex(randn(Nre,Ns,Nr),randn(Nre,Ns,Nr));

Apply OFDM equalization to the 2-D signal contained in an 120-by-8 symbol array.

[eqsym2d,csi2d] = ofdmEqualize(rxsym2d,Hest,nvar,DataFormat="2-D");

Reshape the 2-D signal to a 30-by-4-by-8 symbol array. Apply OFDM equalization to the 3-D signal. Compare the results of OFDM equalization for the 30-by-4-by-8 symbol array with OFDM equalization for the 120-by-8 symbol array. As the isequal function result shows, the equalized symbols and soft channel state information returned for the 30-by-4-by-8 and 120-by-8 symbol arrays are equal.

rxsym3d = reshape(rxsym2d,30,4,Nr);
[eqsym3d,csi3d] = ofdmEqualize(rxsym3d,Hest,nvar,DataFormat="3-D");
isequal(eqsym3d,reshape(eqsym2d,30,4,Ns))

ans = logical
   1

isequal(csi3d,csi2d)

ans = logical
   1

Reshape the 2-D signal to a 60-by-2-by-8 symbol array. Apply OFDM equalization to the 3-D signal. Compare the results of OFDM equalization for the 60-by-2-by-8 symbol array with OFDM equalization for the 120-by-8 symbol array. The isequal function result confirms the equalized symbols and soft channel state information returned for the 60-by-2-by-8 and 120-by-8 symbol arrays are equal.

rxsym3d2 = reshape(rxsym2d,60,2,Nr);
[eqsym3d2,csi3d2] = ofdmEqualize(rxsym3d2,Hest,nvar,DataFormat="3-D");
isequal(eqsym3d2,reshape(eqsym2d,60,2,Ns))

ans = logical
   1

isequal(csi3d2,csi2d)

ans = logical
   1