Main Content

ofdmPrecode

Precode MIMO-OFDM input data

Since R2024b

collapse all in page

Syntax

out = ofdmPrecode(in,P)

Description

out = ofdmPrecode(in,P) precodes an input data signal, in, with a precoding matrix or array, P.

example

Examples

collapse all

Open Live Script

This example creates a precoding matrix using the channel coefficients from a static 2-by-2 MIMO channel. This process allows MIMO transmissions without interference. It sends precoded data across the channel. Then, it uses effective channel estimates to recover this data, showing a transmission without errors.

rng(1);
Nss = 2;    % number of data streams
Ntx = Nss;  % number of transmit chains
Nrx = Nss;  % number of receive chains
Nsym = 7;   % number of data symbols per frame
Nfft = 64;  % OFDM FFT length
Ncp = 16;   % cyclic prefix length for OFDM modulator

Use the comm.MIMOChannel System object to form a static MIMO channel. Keep the channel static by setting the Doppler shift to zero. Use the channel taps from the System object to obtain the channel matrix.

mimoChannel = comm.MIMOChannel(PathGainsOutputPort=true, ...
    SpatialCorrelationSpecification="None", ...
    NumTransmitAntennas=Ntx, ...
    NumReceiveAntennas=Nrx, ...
    MaximumDopplerShift=0);
[~,chTaps] = mimoChannel(complex(zeros(1,2),zeros(1,2))); % step the object to get the channel taps
H = squeeze(chTaps(1,1,:,:));

Break down the channel matrix with singular value decomposition (SVD) to find the precoding matrix and the effective channel matrix. Use the effective channel matrix to equalize the received signal and recover the data symbols.

[U,S,V] = svd(H);
P = U';                           % Use U' as the precoding matrix
Heff = repmat(inv(V/S),1,1,Nfft); % Use inv(V/S) as the effective channel estimate
Heff = permute(Heff,[3 1 2]);     % Permute Heff to be Nfft-by-Nss-by-Ntx

Create data symbols, apply precoding, and transmit the precoded symbols using OFDM through the MIMO channel. Then, demodulate and equalize to retrieve the data symbols.

data = randi([0 1],2*Nfft*Nsym*Nss,1);        % Create serial data stream
x = pskmod(data,4,pi/4,InputType="bit");      % Generate QPSK data symbols
frame = reshape(x,Nfft,Nsym,Nss);             % Reshape to form OFDM grid
precodeOut = ofdmPrecode(frame,P);            % Precode the data symbols
txOut = ofdmmod(precodeOut,Nfft,Ncp);         % OFDM modulate the precoded symbols
chanOut = mimoChannel(txOut);                 % Transmit through the MIMO channel
rxIn = awgn(chanOut,50);                      % Add 50 dB of AWGN
rxSym = ofdmdemod(rxIn,Nfft,Ncp);             % OFDM-demodulate the received signals
eqOut = ofdmEqualize(rxSym,Heff);             % Equalize the symbols
y = reshape(eqOut,[],1);                      % Serialize the symbols
rxData = pskdemod(y,4,pi/4,OutputType="bit"); % Decode the symbols using QPSK

Show that the received data is recovered perfectly without any errors.

constDiag = comm.ConstellationDiagram;
constDiag(y);

fprintf('Bit errors = %d\n',biterr(rxData,data));
Bit errors = 0
Open Live Script

This example shows how to compute precoding matrices for each subcarrier in an OFDM-MIMO system. It uses channel estimates from a static, frequency-selective 2-by-2 MIMO channel. The goal is to enable interference-free MIMO transmission. You send precoded data over the channel and recover it using effective channel estimates to achieve error-free transmission.

rng(1);
Nss = 2;    % number of data streams
Ntx = Nss;  % number of transmit chains
Nrx = Nss;  % number of receive chains
Nsym = 7;   % number of data symbols per frame
Nfft = 64;  % OFDM FFT length
Ncp = 16;   % OFDM cyclic prefix length

Channel Sounding

To find the coefficiets of the MIMO channel matrix coefficients, one transmit antenna sends out a reference signal. Both the transmitter and receiver know this signal. Meanwhile, the other transmit antennas send nothing. This way, the receiving antennas get a clear signal to measure the channel coefficients accurately.

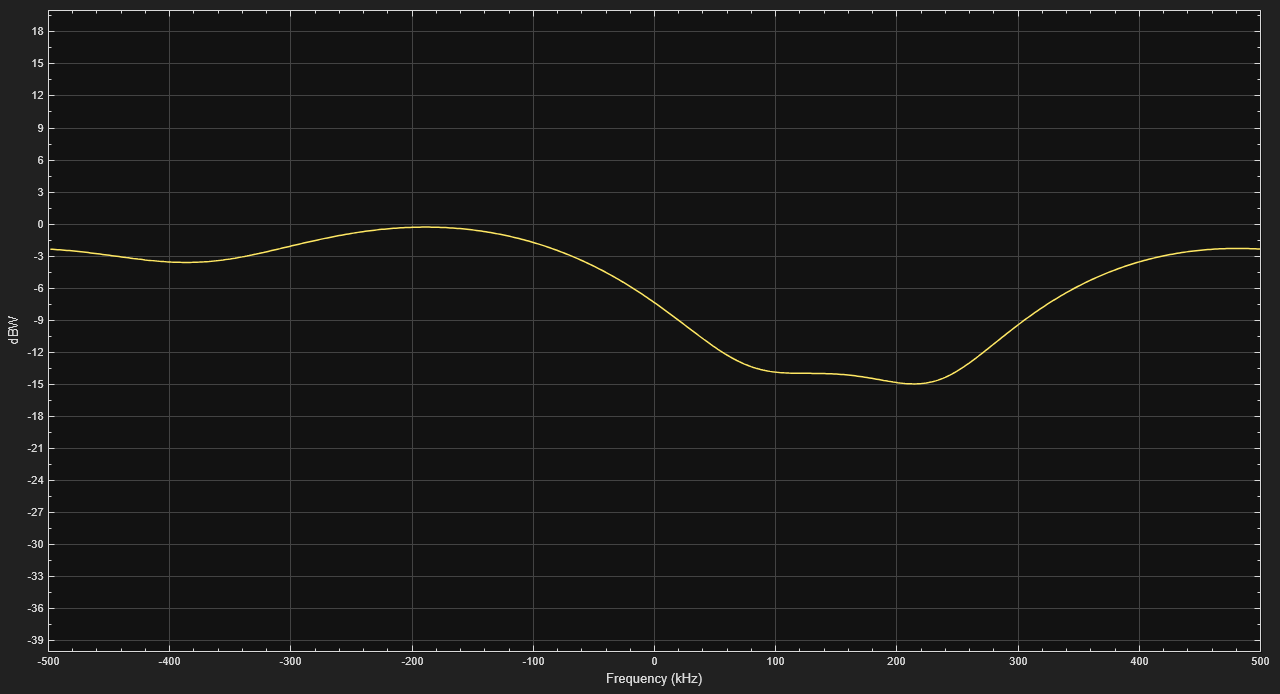
Create a static, frequency-selective MIMO channel using the comm.MIMOChannel System object. To keep the channel unchanged, set the Doppler shift to zero. Introduce path delays to make the channel frequency-selective. Turn on visualization for the channel from transmit antenna 1 to receive antenna 1. In the resulting frequency response, you can see that each subcarrier goes through a different channel response and each subcarrier needs its own precoding matrix.

mimoChannel = comm.MIMOChannel( ...
    MaximumDopplerShift=0, ...
    SpatialCorrelationSpecification="None", ...
    NumTransmitAntennas=Ntx, ...
    NumReceiveAntennas=Nrx, ...
    SampleRate=1e6, ...
    PathDelays=[0 1e-6 3e-6], ...
    AveragePathGains=[0 -6 -9], ...
    Visualization="Frequency Response");

MIMO Channel Sounding

For MIMO channel sounding, use an OFDM reference signal to map the channel across all subcarriers and antennas. To find the channel coefficients h11 and h12, send a reference signal from antenna 1 and keep antenna 2 silent.

H = zeros(Nfft,Ntx,Nrx);                      % MIMO channel matrix
ref = pskmod(randi([0 3],Nfft,1,Ntx),4,pi/4); % Generate QPSK reference symbol
ref(:,1,2) = zeros(Nfft,1);                   % Silence tx antenna 2
txOut = ofdmmod(ref,Nfft,Ncp);                % OFD-modulate the symbols
rxIn = mimoChannel(txOut);                    % Sound the MIMO channel
rxSym = ofdmdemod(rxIn,Nfft,Ncp);             % OFDM-demodulate the symols
H(:,1,:) = rxSym(:,1,:) ./ ref(:,1,1);        % Estimate channel using least-squares

Repeat the sounding process to obtain the channel coefficients h21 and h22 by transmitting a reference signal from antenna 2 while keeping antenna 1 silent.

ref = pskmod(randi([0 3],Nfft,1,Ntx),4,pi/4); % Generate QPSK reference symbol
ref(:,1,1) = zeros(Nfft,1);                   % Silence tx antenna 1
txOut = ofdmmod(ref,Nfft,Ncp);                % OFDM-modulate the symbols
rxIn = mimoChannel(txOut);                    % Sound the MIMO channel
rxSym = ofdmdemod(rxIn,Nfft,Ncp);             % OFDM-demodulate the symbols
H(:,2,:) = rxSym(:,1,:) ./ ref(:,1,2);        % Estimate channel using least-squares

Break down the channel matrices for each subcarrier using singular value decomposition (SVD). This step gives you the precoding matrix and the effective channel matrix for that subcarrier. Use the effective channel matrix to balance the received signal and retrieve the data symbols.

P = zeros(Nss,Ntx,Nfft);     % Precoding array
Heff = zeros(Nfft,Nrx,Nss);  % Effective channel array
for sc = 1:Nfft
    [U,S,V] = svd(squeeze(H(sc,:,:)));
    P(:,:,sc) = U';          % Use U' as the precoding matrix
    Heff(sc,:,:) = inv(V/S); % Use inv(V/S) as the effective channel estimate
end

Create data symbols, apply precoding, and send them through the MIMO channel using OFDM. 

data = randi([0 1],2*Nfft*Nsym*Nss,1);        % Create serial data stream
x = pskmod(data,4,pi/4,InputType="bit");      % Generate QPSK data symbols
frame = reshape(x,Nfft,Nsym,Nss);             % Reshape to form OFDM grid
precodeOut = ofdmPrecode(frame,P);            % Precode the data symbols
txOut = ofdmmod(precodeOut,Nfft,Ncp);         % OFDM-modulate the precoded symbols
chanOut = mimoChannel(txOut);                 % Transmit through the MIMO channel

Then, demodulate and equalize the signal to get back the data symbols.

rxIn = awgn(chanOut,60);                      % Add 60 dB of AWGN
rxSym = ofdmdemod(rxIn,Nfft,Ncp);             % OFDM-demodulate the received signals
eqOut = ofdmEqualize(rxSym,Heff);             % Equalize the symbols
y = reshape(eqOut,[],1);                      % Serialize the symbols
rxData = pskdemod(y,4,pi/4,OutputType="bit"); % Decode the symbols using QPSK

Show that the output constellation is free of interference.

constDiag = comm.ConstellationDiagram;
constDiag(y);

Show that the received data is recovered without error.

fprintf('Bit errors = %d\n',biterr(rxData,data));
Bit errors = 0

Input Arguments

collapse all

OFDM input data, specified as an array of real or complex values of size Nsc-by-Nsym-by-Nss where,

  • Nsc is the number of precoded subcarriers.

  • Nsym is the number of OFDM data symbols.

  • Nss is the number of spatial streams.

Data Types: single | double
Complex Number Support: Yes

Precoder matrix, specified as a matrix of size Nss-by-Ntxchains or an array of precoder matrices of size Nss-by-Ntxchains-by-Nsc, where Ntxchains is the number of transmit chains.

  • When P is a matrix, it is used across all Nsc subcarriers.

  • When P is an array of precoder matrices, each nth matrix in P(:,:,n) is applied to the nth data subcarrier in in.

Data Types: single | double
Complex Number Support: Yes

Output Arguments

collapse all

Precoded output symbols, returned as an array of size Nss-by-Ntxchains-by-Nsc where,

  • Nss is the number of spatial streams.

  • Ntxchains is the number of transmit chains.

  • Nsc is the number of precoded subcarriers.

Algorithms

collapse all

MIMO Overview

MIMO transmission takes advantage of channels that have a large number of multipath signals between the transmitter and receiver. You can mathematically decompose the channel and consider each of the multipath as independent data paths. These data paths increase the channel capacity of the transmission system. Now you can transmit multiple independent data streams over each path with reduced interference between the paths.

Using Ntxchains antennas, the MIMO transmitter creates up to Ntxchains data streams. Let the number of data streams be Nss, where Nss ≤ Ntxchains. After the mathematical decomposition of the channel, the 1-by-Nss is transformed rotationally through a matrix multiplication of a precoding matrix with the input data signal. This rotation of the data across the Nss dimensions reduces the correlation between the data significantly, depending on the richness of the multiple data paths. If Nss < Ntxchains, the precoding matrix increases the dimensionality of the signal to send Nss data streams through Ntxchains antennas, taking advantage of a high-rank channel (a channel that can support many independent data paths).

Mathematically, for a single carrier signal, you precode 1-by-Nss data stream d by an Nss-by-Ntxchains matrix P to get a precoder output y = d*P. For multicarrier modulation, the data streams and precoding matrices operate independently on a per-subcarrier basis.

Version History

Introduced in R2024b

See Also

|

Topics