Phase Noise

Apply receiver phase noise to complex baseband signal

Libraries:
Communications Toolbox / RF Impairments and Components

Description

The Phase Noise block adds phase noise to a complex signal. This block emulates impairments introduced by the local oscillator of a wireless communication transmitter or receiver. The block generates filtered phase noise according to the specified spectral mask and adds it to the input signal. For a description of the phase noise modeling, see Algorithms.

Examples

expand all

Phase Noise Effects on 16-QAM in Simulink

This example uses:

Open Model

Add a phase noise vector and frequency offset vector to a 16-QAM signal. Display the constellation.

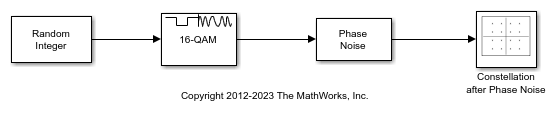
The slex_PhaseNoise16QAM model generates random data, applies 16-QAM modulation to the data, and adds phase noise to the signal. The Phase Noise block specifies a spectral mask with phase noise levels of –40 dBc/Hz at 100 Hz and –70 dBc/Hz at 200 Hz.

The constellation diagram shows a reference 16-QAM constellation and the signal samples impaired by phase noise.

View Phase Noise Effects on Signal Spectrum in Simulink

This example uses:

Open Model

This example shows the effects that spectral and phase noise have on a 100 kHz sine wave.

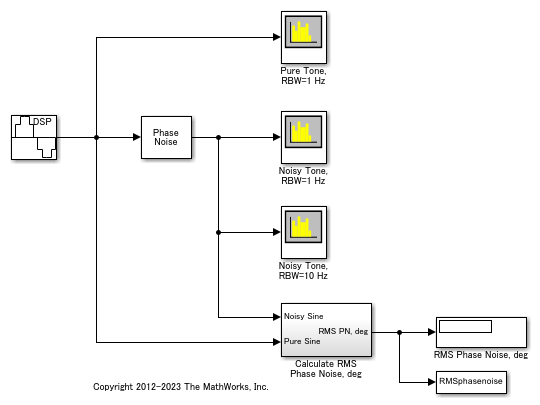
The slex_phasenoise model generates a 100 kHz tone by using a Sine Wave block and adds phase noise at these frequencies by using a Phase Noise block.

-85 dBc/Hz at a frequency offset of 1e3 Hz
-118 dBc/Hz at a frequency offset of 9.5e3 Hz
-125 dBc/Hz at a frequency offset of 19.5e3 Hz
-145 dBc/Hz at a frequency offset of 195e3 Hz

To analyze the spectrum and phase noise, the model includes three Spectrum Analyzer blocks configured for the dBW/Hz view:

Pure Tone, RBW=1 Hz — 1 Hz resolution bandwidth
Noisy Tone, RBW=1 Hz — 1 Hz resolution bandwidth
Noisy Tone, RBW=10 Hz — 10 Hz resolution bandwidth

The model also includes a subsystem to calculate the RMS phase noise. The subsystem that calculates the RMS phase noise finds the phase error between the pure and noisy sine waves, then calculates the RMS phase noise in degrees. In general, to accurately determine the phase error, the pure signal must be time aligned with the noisy signal. However, the periodicity of the sine wave in this model makes this step unnecessary.

The model displays the signal spectrum and outputs the average of the calculated phase noise. The calculated phase noise achieves the spectrum defined by the Phase Noise block.

When the model runs, it displays the signal spectrum and outputs the average of the calculated phase noise. The calculated phase noise achieves the spectrum defined by the Phase Noise block.

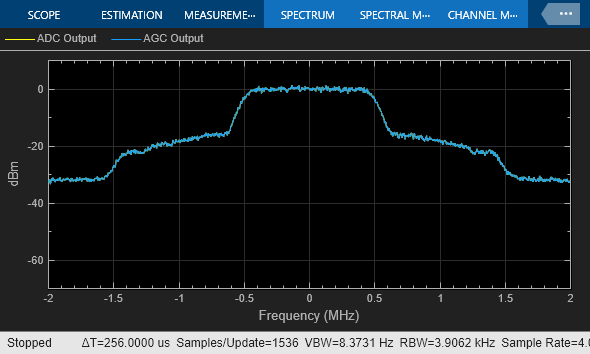
With the resolution bandwidth set to 1 Hz, the dBW/Hz view for the spectrum analyzer shows the tone at 0 dBW/Hz. With the resolution bandwidth set to 10 Hz, the dBW/Hz view for the spectrum analyzer shows the tone at -10 dBW/Hz. That same tone energy is now spread across 10 Hz instead of 1 Hz, so the sine wave PSD level reduces by 10 dB. With the resolution bandwidth at 10 Hz, the displayed average of the calculated phase noise still achieves the phase noise defined by the Phase Noise block.

The Spectrum Analyzer block achieves better spectral averaging with the wider resolution bandwidth. For more information, see Windows.

The calculated average phase noise is 0.37 degrees.

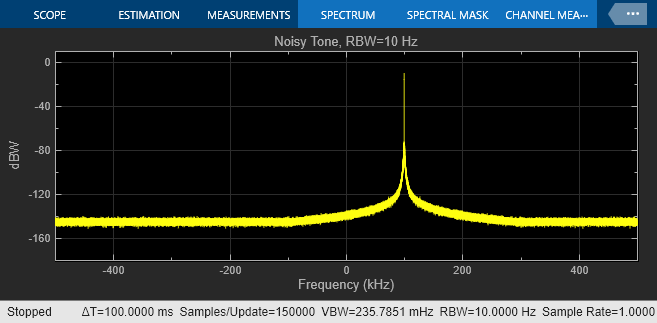
To explore further, you can change the Phase noise level (dBc/Hz) parameter in the Phase Noise block, rerun the model, and notice how the spectrum shape changes. With more noise, the side lobes increase in amplitude. As more phase noise is added, the 100 Hz signal becomes less distinct and the measured RMS phase noise increases.

Extended Examples

Impact of RF Effects on Communication System Performance

Model thermal noise, phase noise, and nonlinearity impairments of an RF transceiver in Simulink^®.

Open Script

Ports

Input

expand all

In — Input signal
vector | matrix

Input signal, specified as an N_S-by-1 numeric vector or N_S-by-M numeric matrix. N_S represents the number of samples and M is the number of channels.

Data Types: double | single
Complex Number Support: Yes

Output

expand all

Out — Output signal
vector | matrix

Output signal, returned as a complex-valued signal with the same data type and size as the input signal.

Parameters

expand all

To edit block parameters interactively, use the Property Inspector. From the Simulink Toolstrip, on the Simulation tab, in the Prepare gallery, select Property Inspector.

Phase noise level (dBc/Hz) — Phase noise level
`[-80 -100]` (default) | vector of negative scalars

Phase noise level in decibels relative to carrier per hertz (dBc/Hz), specified as a vector of negative scalars. The Phase noise level (dBc/Hz) and Frequency offset (Hz) parameters must have the same length.

Frequency offset (Hz) — Frequency offset
`[2000 20000]` (default) | vector of positive increasing values

Frequency offset in Hz, specified as a vector of positive increasing values. The maximum frequency offset value must be less than F_S / 2, where F_S represents the Sample rate (Hz) parameter value.

The Phase noise level (dBc/Hz) and Frequency offset (Hz) parameters must have the same length.

Sample rate (Hz) — Sample rate
`1e6` (default) | positive scalar

Sample rate in Hz, specified as a positive scalar greater than two times the maximum value specified by the Frequency offset (Hz) parameter.

Initial seed — Initial seed of noise generator
`2137` (default) | positive scalar

Initial seed of noise generator, specified as a positive scalar.

This block uses the Random Source block to generate noise. The block generates random numbers using the Ziggurat method (V5 RANDN algorithm). Every time you rerun the simulation, the block reuses the same initial seed. That way, the block outputs the same signal each time you run a simulation.

View Filter Response — Display magnitude response of filter
button

Display magnitude response of filter defined by the block.

Simulate using — Type of simulation to run
`Interpreted execution` (default) | `Code generation`

Type of simulation to run, specified as Interpreted execution or Code generation.

Interpreted execution — Simulate the model by using the MATLAB^® interpreter. This option requires less startup time, but the speed of subsequent simulations is slower than with the Code generation option. In this mode, you can debug the source code of the block.
Code generation — Simulate the model by using generated C code. The first time you run a simulation, Simulink generates C code for the block. The model reuses the C code for subsequent simulations unless the model changes. This option requires additional startup time, but the speed of the subsequent simulations is faster than with the Interpreted execution option.

For more information, see Interpreted Execution vs. Code Generation (Simulink).

Block Characteristics

Data Types	`double` \| `single`
Multidimensional Signals	`no`
Variable-Size Signals	`no`

Algorithms

expand all

The output signal, y_k, is related to input sequence x_k by y_k=x_ke^jφ_k, where φ_k is the phase noise. The phase noise is filtered Gaussian noise such that φ_k=f(n_k), where n_k is the noise sequence and f represent a filtering operation.

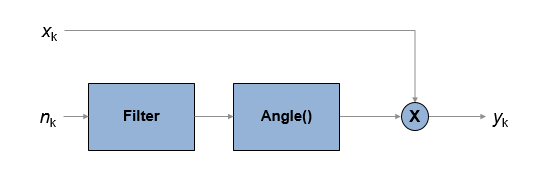
Diagram showing phase noise applied to input signal

To model the phase noise, define the power spectrum density (PSD) mask characteristic by specifying scalar or vector values for the frequency offset and phase noise level.

For a scalar frequency offset and phase noise level specification, an IIR digital filter computes the spectrum mask. The spectrum mask has a 1 / f characteristic that passes through the specified point. For more information, see IIR Digital Filter.
For a vector frequency offset and phase noise level specification, an FIR filter computes the spectrum mask. The spectrum mask is interpolated across log10(f). For more information, see FIR Filter.

IIR Digital Filter

For the IIR digital filter, the numerator coefficient is

$λ = \sqrt{2 π f_{o f f s e t} 10^{L / 10}},$

where f_offset is the frequency offset in Hz and L is the phase noise level in dBc/Hz. The denominator coefficients, γ_i, are recursively determined as

$γ_{i} = (i - 2.5) \frac{γ_{i - 1}}{i - 1},$

where γ₁ = 1, i = {1, 2,..., N_t}, and N_t is the number of filter coefficients. N_t is a power of 2 in the range [2⁷, 2¹⁹]. The value of N_t grows as the phase noise offset decreases towards 0 Hz.

FIR Filter

For the FIR filter, the phase noise level is determined through log10(f) interpolation for frequency offsets over the range [df, f_s / 2], where df is the frequency resolution and f_s is the sample rate. The phase noise is flat over the range [0, df] in Hz, and from the largest frequency offset to f_s / 2. The phase noise has 1 / f³ characteristic from df to the smallest frequency offset. The phase noise is linearly interpolated between the smallest and the largest frequency offset. The frequency resolution is equal to (f_s / 2)(1 / N_t), where N_t is the number of coefficients, and is a power of 2 less than or equal to 2¹⁶.

Use a time domain FIR filter if the number of taps, N_t, of the resulting filter is less than 2⁸. Use a frequency domain FIR filter if 2⁸ <= N_t <= 2¹⁶. Use a cascaded system of filters and synthesizers if N_t > 2¹⁶. Divide the [0, f_s/2] frequency range into two equal halves. Design a filter to shape the phase noise in each sub band. Combine the two sub bands using a synthesizer that results in the desired phase noise characteristics over the [0, f_s/2] range. Repeat this process for each sub band until the number of taps of each filter is less than or equal to2¹⁶.

The single filter, or the cascaded filter-synthesizer system, is primed during initialization to remove filter latency.

References

[1] Kasdin, N. J. "Discrete Simulation of Colored Noise and Stochastic Processes and 1/(f^alpha); Power Law Noise Generation." The Proceedings of the IEEE^® 83, no. 5 (May, 1995): 802–27.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

Introduced before R2006a

expand all

R2024a: Model high frequency phase noise impairment

Use the Phase Noise block to accurately model phase noise at higher frequency signals. Use the View Filter Response button on Phase Noise block mask to verify the accuracy of the realized phase noise.

Phase Noise

Description

Examples

Phase Noise Effects on 16-QAM in Simulink

View Phase Noise Effects on Signal Spectrum in Simulink

Extended Examples

Impact of RF Effects on Communication System Performance