加窗法

在数字滤波器设计和频谱估计中，加窗函数的选择对于整体结果的质量有重大影响。加窗的主要作用是减弱因无穷级数截断而产生的吉布斯现象的影响。

Signal Processing Toolbox™ 产品提供两个处理加窗的图形用户界面工具：

有关详细信息，请参见参考页。

基本窗是矩形窗，即由 1 组成的适当长度的向量。以下是一个长度为 50 的矩形窗

n = 50;
w = rectwin(n);

Signal Processing Toolbox 按照惯例将窗存储在列向量中，因此等效的表达式是

w = ones(50,1);

要使用窗设计器创建此窗，请键入

windowDesigner

App 打开并默认加载一个 Hamming 窗。要显示矩形窗，请在“当前窗信息”面板中设置类型 = 矩形和长度 = 50，然后按应用。

Bartlett（或三角形）窗是两个矩形窗的卷积。函数 bartlett 和 triang 相似，都计算三角形窗，但有三个重要区别。bartlett 函数始终返回在序列末尾有两个零的窗，因此对于奇数 n，bartlett(n+2) 的中间部分等效于 triang(n)：

Bartlett = bartlett(7);
isequal(Bartlett(2:end-1),triang(5))

ans =
     1

对于偶数 n，bartlett 仍然是两个矩形序列的卷积。偶数 n 的三角形窗则没有标准定义；在这种情况下，triang 结果的线段斜率比 bartlett 稍陡：

w = bartlett(8); 
[w(2:7) triang(6)]

您可以在窗设计器中看到奇数和偶数 Bartlett 窗的区别。

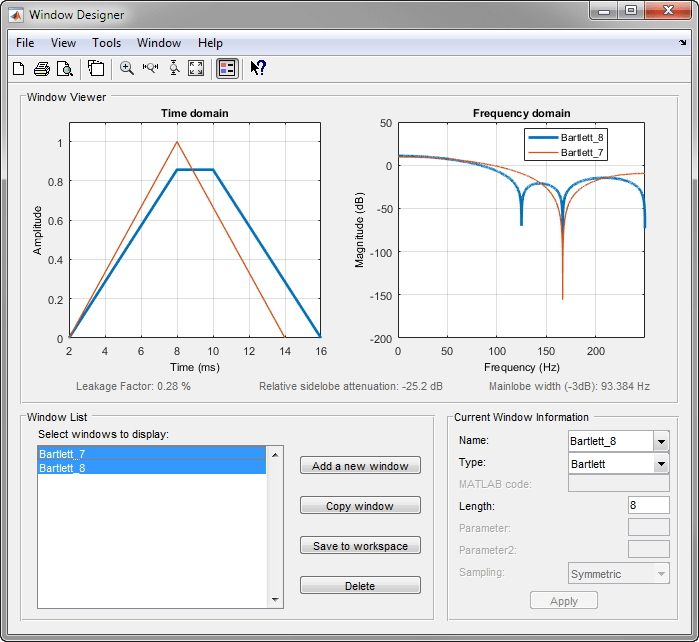
Bartlett 窗和三角形窗之间的最后一个区别可以在这些函数的傅里叶变换中清楚地观察到。对于偶数 n，Bartlett 窗的傅里叶变换为负。然而，三角形窗的傅里叶变换始终为非负。

下图描绘包含 8 个点的 Bartlett 窗和三角形窗的零相位响应，以说明这种差异。

zerophase(bartlett(8))
hold on
zerophase(triang(8))
legend('Bartlett','Triangular')
axis([0.3 1 -0.2 0.5])

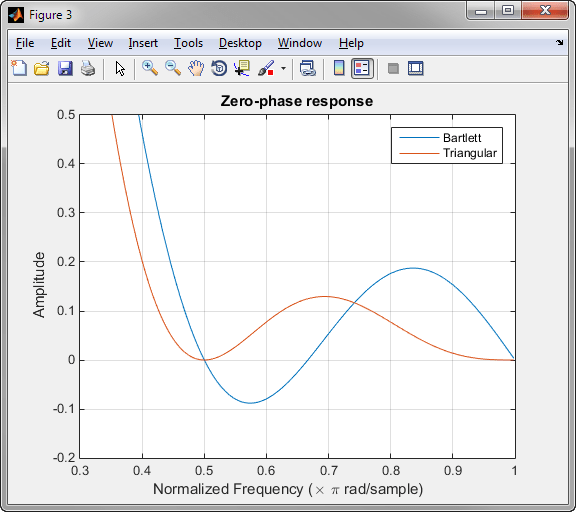
当为某些频谱估计方法（如 Blackman-Tukey 方法）选择窗时，这一差异可能会很关键。Blackman-Tukey 通过计算自相关序列的傅里叶变换来形成频谱估计值。如果窗的傅里叶变换为负值，则在某些频率下得到的估计值可能是负值。

另请参阅