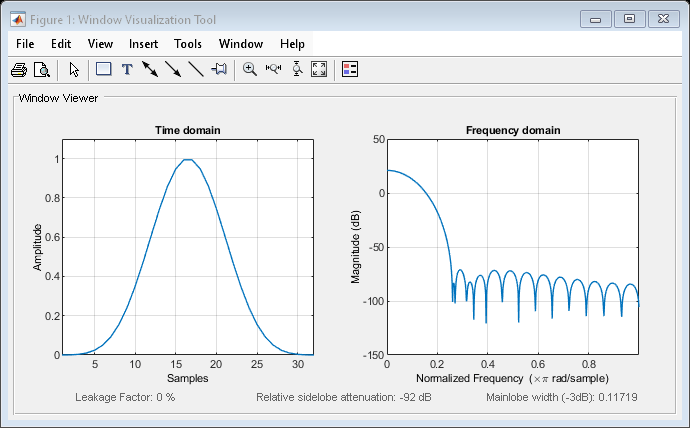
blackmanharris

最小四项布莱克曼-哈里斯窗

全页折叠

语法

w = blackmanharris(N)

w = blackmanharris(N,sflag)

说明

w = blackmanharris(N) 返回一个长度为 N 个点的对称四项布莱克曼-哈里斯窗。

示例

w = blackmanharris(N,sflag) 使用由 sflag 指定的窗采样方法返回一个布莱克曼-哈里斯窗。

示例

全部折叠

布莱克曼-哈里斯窗

打开实时脚本

创建一个长度为 32 个点的对称布莱克曼-哈里斯窗。使用 wvtool 显示结果。

N = 32;
wvtool(blackmanharris(N))

输入参数

全部折叠

`N` — 窗长度
正整数

窗长度，指定为正整数。

数据类型: single | double

`sflag` — 窗采样
`'symmetric'` (默认) | `'periodic'`

窗采样方法，指定为：

'symmetric' - 在使用窗进行滤波器设计时使用此选项。
'periodic' - 此选项对于频谱分析很有用，因为它使加窗信号可具有离散傅里叶变换中固有的完美周期延拓。当指定 'periodic' 时，该函数计算长度为 L + 1 的窗，并返回前 L 个点。

输出参量

全部折叠

`w` — 布莱克曼-哈里斯窗
列向量

布莱克曼-哈里斯窗，以列向量形式返回。

算法

长度为 N 的对称四项布莱克曼-哈里斯窗的方程为

$w (n) = a_{0} - a_{1} \cos (\frac{2 π n}{N - 1}) + a_{2} \cos (\frac{4 π n}{N - 1}) - a_{3} \cos (\frac{6 π n}{N - 1}), 0 \leq n \leq N - 1$

长度为 N 的周期性四项布莱克曼-哈里斯窗的方程为：

$w (n) = a_{0} - a_{1} \cos \frac{2 π n}{N} + a_{2} \cos \frac{4 π n}{N} - a_{3} \cos \frac{6 π n}{N}, 0 \leq n \leq N - 1$

周期性窗以长度 N 为周期。

系数	值
a₀	0.35875
a₁	0.48829
a₂	0.14128
a₃	0.01168

参考

[1] harris, fredric j. “On the Use of Windows for Harmonic Analysis with the Discrete Fourier Transform.” Proceedings of the IEEE^®. Vol. 66, January 1978, pp. 51–83.

扩展功能

C/C++ 代码生成
使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

版本历史记录

在 R2006a 之前推出

另请参阅

App

窗设计器

函数

barthannwin | bartlett | bohmanwin | nuttallwin | parzenwin | rectwin | triang | WVTool

blackmanharris

语法

说明

示例

布莱克曼-哈里斯窗

输入参数

N — 窗长度 正整数

sflag — 窗采样 'symmetric' (默认) | 'periodic'

输出参量

w — 布莱克曼-哈里斯窗 列向量

算法

参考

扩展功能

C/C++ 代码生成 使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

版本历史记录

另请参阅

App

函数

WeChat

`N` — 窗长度
正整数

`sflag` — 窗采样
`'symmetric'` (默认) | `'periodic'`

`w` — 布莱克曼-哈里斯窗
列向量

C/C++ 代码生成
使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。