Spreading Sequences

Spreading consists of multiplying input data bits by a pseudorandom or pseudonoise (PN) sequence. The ratio of the PN sequence bit rate to the data rate is called the spreading factor. When the PN sequence has a bit rate higher than the data bit rate, the spreading factor is greater than 1. When the spreading factor is greater than 1, spreading input data adds redundancy to the transmission signal.

Spreading input data by using spreading sequences with low cross-correlation properties enables the receiver to resolve individual user data after despreading the received signal. Using spreading sequences with low cross-correlation properties helps resolve individual user data in a multipath environment in the presence of interference signals.

After signal synchronization on the receiver side, the received signal is multiplied by the same PN that was used by the transmitter. This operation removes the spreading from the received signal. Ideally, after this despreading, the signal for the user of interest is recovered with no further contribution by the signals of interferers. In CDMA systems, each transmitter is assigned distinct spreading codes that have low cross-correlation properties, such as the ideal orthogonal codes or any one of the PN, Gold, or Kasami sequences.

Spread-spectrum communication systems spread the transmission signal over a wide frequency band, typically much wider than the minimum bandwidth required to transmit the data. The spreading uses a waveform that appears random to anyone except the intended receiver of the transmitted signal. The waveform is actually pseudorandom in the sense that it can be generated by precise rules, yet has the statistical properties of a truly random sequence.

The following sections highlight various spreading sequences, their properties, and characteristic performance in single-user or multiuser and single-path or multipath transmission environments.

Orthogonal Spreading for Multiuser System in Single-Path Channel

This example uses:

Open Model

This model compares data recovery for a single-user system versus a two-user system. Transmission data passes through a single-path AWGN channel in two data streams that are independently spread by different orthogonal codes.

The model uses random binary data, which is BPSK modulated (real), spread by orthogonal codes of length 64, and then transmitted over an AWGN channel. The receiver consists of a despreader followed by a BPSK demodulator.

Using the same transmission data, the model calculates the BER performance for recovery of the single-user and two-user transmissions through identically configured AWGN channels.

The bit error rate results are exactly the same for the individual users in both cases. The matching error rates result from perfect despreading due to the ideal cross-correlation properties of the orthogonal codes selected.

To experiment further, open the model. Modify the settings to see how the performance varies with different Hadamard codes for the individual users.

Orthogonal Spreading for Single-User System in Multipath Channel

This example uses:

Open Model

This model simulates orthogonal spreading for a single-user system in a multipath transmission environment. This is similar to a mobile channel environment where the signals are received over multiple paths. Each path can have different amplitudes and delays. The receiver combines the independent paths coherently by using diversity reception to realize gains from the multipath transmissions received. The modeled system does not simulate fading effects and the receiver gets perfect knowledge of the number of paths and their respective delays.

The model uses random binary data, which is BPSK modulated (real), spread by orthogonal codes of length 64, and then transmitted over a multipath AWGN channel. The receiver consists of a despreader, a diversity combiner, and a BPSK demodulator.

The non-ideal, auto-correlation values of the chosen orthogonal spreading codes prevent perfect resolution of the individual paths. As a consequence, BER performance is not improved by using diversity combining in the receiver. For a multipath example that uses PN sequences when spreading user data and uses diversity combining in the receiver, see PN Spreading for Single-User System in Multipath Channel.

To experiment further, open the model. Modify the settings to see how the performance varies for different path delays or with different Hadamard codes.

PN Spreading for Single-User System in Multipath Channel

This example uses:

Open Model

This model simulates pseudo-random spreading for a single-user system in a multipath transmission environment. This is similar to a mobile channel environment where the signals are received over multiple paths. Each path can have different amplitudes and delays. The receiver combines the independent paths coherently by using diversity reception to realize gains from the multipath transmissions received. The modeled system does not simulate fading effects and the receiver gets perfect knowledge of the number of paths and their respective delays.

The model uses random binary data, which is BPSK modulated (real), spread by PN sequences, and then transmitted over a multipath AWGN channel. The receiver consists of a despreader, a diversity combiner, and a BPSK demodulator. The receiver achieves gains from diversity combining due to the ideal auto-correlation properties of the PN sequences used when spreading the data.

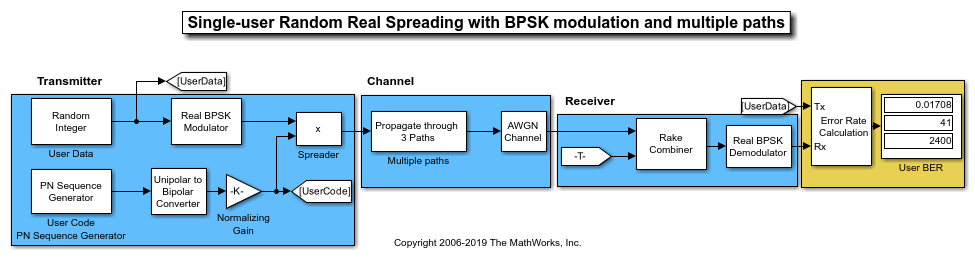
To experiment further, open the model. Modify the settings to see how the performance varies for different path delays or adjust the PN sequence generator parameters.

PN Spreading for Multiuser System in Multipath Channel

This example uses:

Open Model

This model simulates pseudo-random spreading for two users in a multipath transmission environment. This is similar to a mobile channel environment where the signals are received over multiple paths. Each path can have different amplitudes and delays. The receiver combines the independent paths coherently using diversity reception to realize gains from the multipath transmissions received. The modeled system does not simulate fading effects and the receiver gets perfect knowledge of the number of paths and their respective delays.

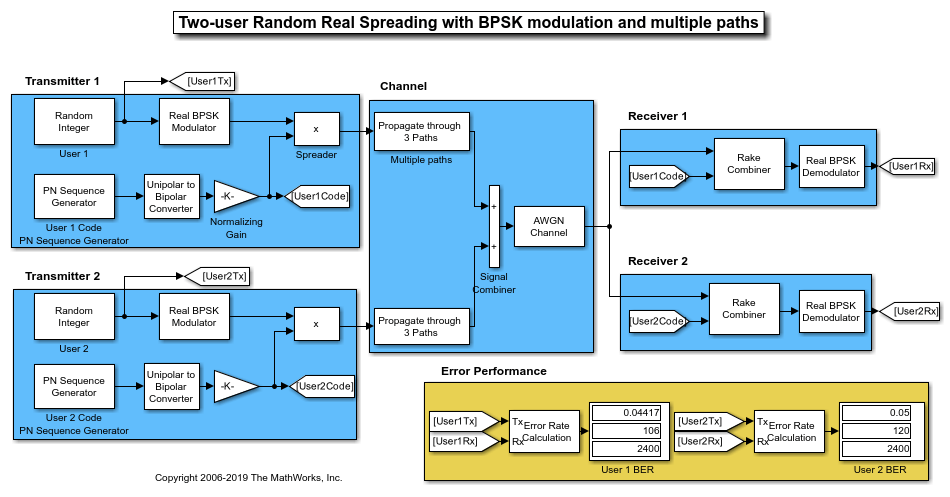
Using the same transmission data, the model calculates the performance for two-user transmissions through identically configured, multipath AWGN channels.

Because the transmissions for the individual users were spread using different PN sequences, the error rate computed for the users are different. Due to the higher cross-correlation properties of the nonorthogonal PN sequences used to spread the data, BER performance is degraded in a multipath environment. Sequences with high orthogonality, such as Hadamard and Kasami, are a better choice for multipath environments. For a multipath example that uses Hadamard code sequences when spreading user data, see Orthogonal Spreading for Multiuser System in Single-Path Channel. For a multipath example that uses Kasami code sequences when spreading user data, see Kasami Spreading for Multiuser System in Multipath Channel.

To experiment further, open the model. Modify the settings to see how the performance varies for different path delays or with different PN sequences for the individual users.

Benefits of Diversity Combining for Nonorthogonal Sequence Spreading

For the PN Spreading for Multiuser System in Multipath Channel example, the individual user performance is degraded for the same channel conditions that were used in the PN Spreading for Single-User System in Multipath Channel example. This is primarily due to the higher cross-correlation values between the two sequences, which prevent ideal separation. However, there are still advantages to diversity combining when using nonorthogonal sequence spreading, because the error rate for a multipath AWGN channel received using RAKE with diversity combining is nearly as good as the AWGN-only case in the Orthogonal Spreading for Multiuser System in Single-Path Channel example.

Kasami Spreading for Multiuser System in Multipath Channel

This example uses:

Open Model

This model simulates Kasami sequence spreading for two users in a multipath transmission environment. This is similar to a mobile channel environment where the signals are received over multiple paths. Each path can have different amplitudes and delays. The receiver combines the independent paths coherently using diversity reception to realize gains from the multipath transmissions received. The modeled system does not simulate fading effects and the receiver gets perfect knowledge of the number of paths and their respective delays.

The model uses random binary data, which is BPSK modulated (real), spread by Kasami sequences, and then transmitted over a multipath AWGN channel. The receiver consists of a despreader, a diversity combiner, and a BPSK demodulator.

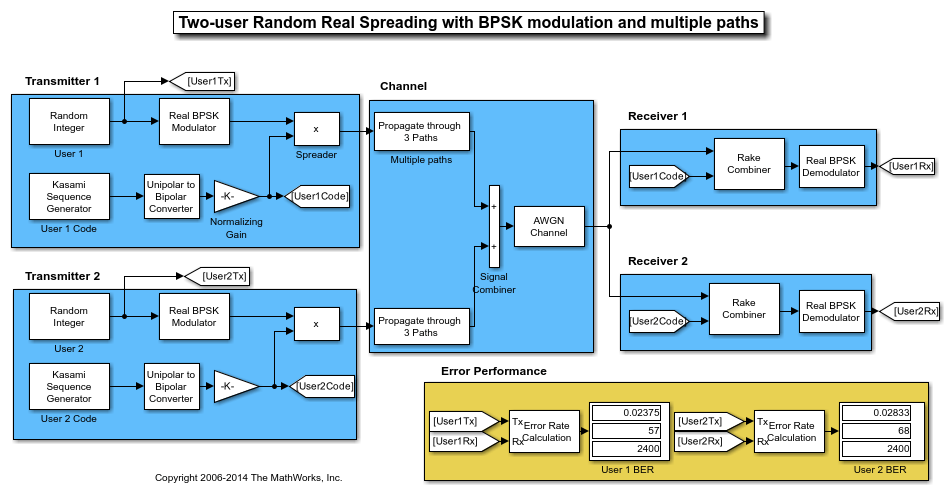
Using the same transmission data, the model calculates the performance for two-user transmissions through identically configured multipath AWGN channels.

The computed BER indicates transmission data spread using Kasami sequences exhibit low cross-correlation. The Kasami sequences provide a balance between the ideal cross-correlation properties of orthogonal codes and the ideal auto-correlation properties of PN sequences.

To experiment further, open the model. Modify the settings to see how the performance varies for different path delays or with different Kasami sequence generator settings for the individual users.