setDelayModel

Construct state-space model with internal delays

Syntax

sys = setDelayModel(H,tau) sys = setDelayModel(A,B1,B2,C1,C2,D11,D12,D21,D22,tau)

Description

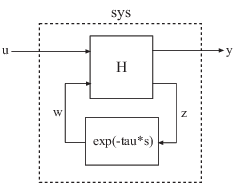
sys = setDelayModel(H,tau) constructs the state-space model sys obtained by LFT interconnection of the state-space model H with the vector of internal delays tau, as shown:

sys = setDelayModel(A,B1,B2,C1,C2,D11,D12,D21,D22,tau) constructs the state-space model sys described by the following equations:

$\begin{matrix} \frac{d x (t)}{d t} = A x (t) + B_{1} u (t) + B_{2} w (t) \\ y (t) = C_{1} x (t) + D_{11} u (t) + D_{12} w (t) \\ z (t) = C_{2} x (t) + D_{21} u (t) + D_{22} w (t) \\ w (t) = z (t - τ) . \end{matrix}$

tau (τ) is the vector of internal delays in sys.

Input Arguments

H

State-space (ss) model to interconnect with internal delays tau.

tau

Vector of internal delays of sys.

For continuous-time models, express tau in seconds.

For discrete-time models, express tau as integer values that represent multiples of the sample time.

A,B1,B2,C1,C2,D11,D12,D21,D22

Set of state-space matrices that, with the internal delay vector tau, explicitly describe the state-space model sys.

Output Arguments

sys

State-space (ss) model with internal delays tau.

Tips

setDelayModel is an advanced operation and is not the natural way to construct models with internal delays. See Time Delays in Linear Systems for recommended ways of creating internal delays.
The syntax sys = setDelayModel(A,B1,B2,C1,C2,D11,D12,D21,D22,tau) constructs a continuous-time model. You can construct the discrete-time model described by the state-space equations
$\begin{matrix} x [k + 1] = A x [k] + B_{1} u [k] + B_{2} w [k] \\ y [k] = C_{1} x [k] + D_{11} u [k] + D_{12} w [k] \\ z [k] = C_{2} x [k] + D_{21} u [k] + D_{22} w [k] \\ w [k] = z [k - τ] . \end{matrix}$
To do so, first construct sys using sys = setDelayModel(A,B1,B2,C1,C2,D11,D12,D21,D22,tau). Then, use sys.Ts to set the sample time.

Version History

Introduced in R2007a