NCFBalancedTruncation
Balanced truncation of normalized coprime factors model order reduction specification
Since R2023b
Description
The NCFBalancedTruncation object stores model order reduction
specifications for the balanced truncation of normalized coprime factors (NCF) of ordinary
(nonsparse) linear time-invariant (LTI) models.
Creation
The reducespec
function creates an NCF balanced truncation model order reduction (MOR) object when you use
this syntax.
R = reducespec(sys,"ncf")Here, sys is any nonsparse LTI model. The workflow uses this object to
set up MOR tasks and store results. For the full workflow, see Task-Based Model Order Reduction Workflow.
This method requires Robust Control Toolbox™ software.
Properties
Object Functions
process | Run model order reduction algorithm |
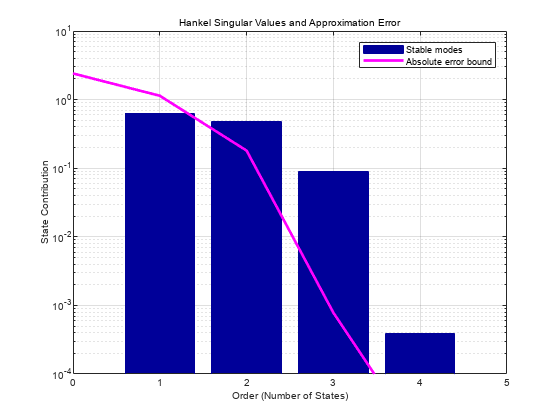
view (ncf) | Plot state contributions when using balanced truncation of normalized coprime factors method |
getrom (ncf) | Obtain reduced-order models when using balanced truncation of normalized coprime factors method |
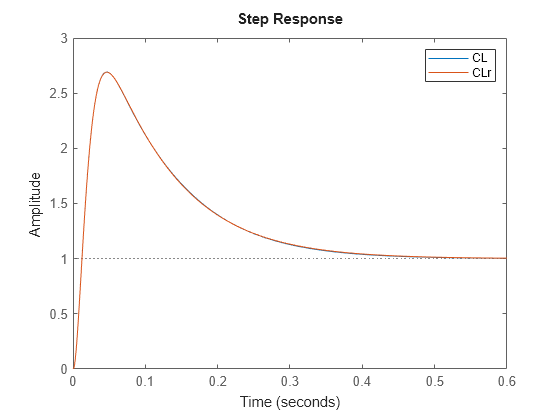
Examples
Tips
You can use this method to reduce the plant G or controller K while preserving closed-loop stability of the following SISO or MIMO feedback loop.
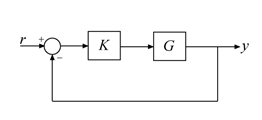
Stability of this loop is preserved as long as the approximation error of the reduced plant is smaller than the robustness margin for this loop given by
ncfmargin(G,K).For controllers computed with
ncfsyn(Robust Control Toolbox), reducing the controller Ks thatncfsyncomputes for the shaped controller Gs is preferable. Both Ks and Gs are returned byncfsynin theinfooutput argument. You can then compute Kr, the reduced controller for the original plant G, from Kr = W1KsrW2, where W1 and W2 are the shaping weights used withncfsyn. For an example, see Reduce Controller Order While Preserving Stability and Robustness.For controllers obtained by other techniques, reduction with this method also preserves stability if the error does not exceed the
ncfmarginmargin. However, such reduction can partially remove integral action and introduce steady-state tracking errors. Therefore, removing any integrator terms from the controller before reduction and replacing them in the reduced controller is recommended.
Algorithms
The balanced truncation of normalized coprime factors algorithm performs these steps to reduce the input model G to the desired order k.
Find the left normalized coprime factorization [Ml,Nl] of
G, whereG= Ml\Nl (seelncf(Robust Control Toolbox)).Obtain the kth-order approximation [Mk,Nk] of [Ml,Nl], using balanced model truncation with absolute error control (see the Algorithms section of
BalancedTruncation).Set
Gred= Mk\Nk.
Version History
Introduced in R2023b
See Also
process | view (ncf) | getrom (ncf) | lncf (Robust Control Toolbox)