Control Design for Spinning Disks

This example uses:

This example shows how to design a gain-scheduled $H_{2}$ controller for a mechanical system consisting of coupled spinning disks described in [1].

Coupled Spinning Disks

A pair of rotating disks is shown in this figure. The slotted disks rotate at rates of $Ω_{1}$ rad/s and $Ω_{2}$ rad/s. The disks contain masses $M_{1}$ and $M_{2}$ , which can move in the horizontal plane and slide radially. The two masses are connected by a wire, coupler, and pulley system that can transmit force in both compression and tension. This coupling system acts as a spring with spring constant $k$ , and friction due to the sliding motion of each mass is modeled by a damping coefficient $b$ .

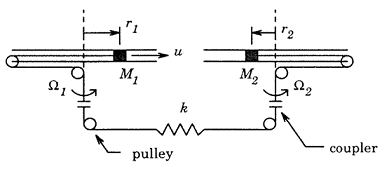
A pair of spinning disks.

The goal is to control the positions of the two masses: $r_{1}$ for mass $M_{1}$ and $r_{2}$ for $M_{2}$ . The control input is a radial force $f_{u}$ acting on mass $M_{1}$ and radial disturbance forces $f_{1}$ and $f_{2}$ act on each mass. The equations of motions are as follows.

$M_{1} (\ddot{r_{1}} - Ω_{1}^{2} r_{1}) + b \dot{r_{1}} + k (r_{1} + r_{2}) = f_{u} + f_{1}$

$M_{2} (\ddot{r_{2}} - Ω_{2}^{2} r_{2}) + b \dot{r_{2}} + k (r_{1} + r_{2}) = f_{2}$

Here:

$M_{1}$ = 1 kg and is the mass of the sliding mass in disk 1.
$M_{1}$ = 2 kg and is the mass of the sliding mass in disk 2.
$b$ = 1 kg/s and is the damping coefficient due to friction.
$k$ = 200 N/m is the spring constant of mass coupling system.
$r_{1} (t)$ is the position of the sliding mass $M_{1}$ relative to the center of disk 1 (m).
$r_{2} (t)$ is the position of the sliding mass $M_{2}$ relative to the center of disk 2 (m).
$Ω_{1} (t)$ is the rotational rate of disk 1 (rad/s).
$Ω_{2} (t)$ is the rotational rate of disk 2 (rad/s).
$f_{u}$ is the control force acting radially on mass $M_{1}$ (N).
$f_{1}$ and $f_{2}$ are the disturbance forces acting radially on $M_{1}$ and $M_{2}$ , respectively (N).

The rotational rates of the spinning disks are allowed to vary in the ranges $Ω_{1} \in [0, 3]$ and $Ω_{2} \in [0, 5]$ (in rad/s). These rates are not known in advance but are measured and available for control design. The objective of the control design is to command the radial position of mass $M_{2}$ . Note that the control input is applied to mass $M_{1}$ and is transmitted to mass $M_{2}$ through the disk coupling system.

LPV Model

The equations of motions are linear except for the rates $Ω_{1}$ and $Ω_{2}$ . Choosing $p_{1} = Ω_{1}^{2}$ , $p_{2} = Ω_{2}^{2}$ , $p_{1} \in [0, 9]$ , and $p_{2} \in [0, 25]$ as scheduling parameters, you obtain the following LPV model of the overall system.

$\dot{x} (t) = [\begin{array}{c} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ p_{1} - \frac{k}{M_{1}} & - \frac{k}{M_{1}} & - \frac{b}{M_{1}} & 0 \\ - \frac{k}{M_{2}} & p_{2} - \frac{k}{M_{2}} & 0 & - \frac{b}{M_{2}} \end{array}] x (t) + [\begin{array}{c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ \frac{1}{M_{1}} & \frac{0.1}{M_{1}} & 0 \\ 0 & 0 & \frac{0.1}{M_{2}} \end{array}] [\begin{array}{c} f_{u} (t) \\ f_{1} (t) \\ f_{2} (t) \end{array}]$

$y (t) = [\begin{array}{c} 0 & 1 & 0 & 0 \end{array}] x (t)$

Here, the state vector $x (t) = [\begin{array}{c} r_{1} (t) \\ r_{2} (t) \\ \dot{r_{1}} (t) \\ \dot{r_{2}} (t) \end{array}]$ .

To create this LPV model, write a function disksGFCN that computes the $A$ , $B$ , $C$ matrices as a function of the scheduling parameters $p = [\begin{array}{c} p_{1} \\ p_{2} \end{array}]$ . To see the code for this function, see the disksGFCN.m file or enter type disksGFCN at the command line.

Define system parameters.

m1 = 1;
m2 = 0.5;
k = 200;
b = 1;

Define the LPV system.

fh = @(t,p) disksGFCN(t,p,m1,m2,k,b);
G = lpvss(["p1","p2"],fh);

Gain-Scheduled H2 Control Design

Design a gain-scheduled $H_{2}$ -optimal controller. First, design an $H_{2}$ -optimal controller at each point on a grid of ( ${Ω_{1}^{2}}_{}$ , $Ω_{2}^{2}$ ) values. For fixed rotational rates, such controllers minimize the closed-loop $H_{2}$ norm from disturbance $d = [\begin{array}{c} f_{1} (t) \\ f_{2} (t) \end{array}]$ to error $e$ for the weighted interconnection. For appropriately selected weights, this interconnection defines the desired $H_{2}$ performance of the control law. The controller takes in the reference $r$ and measurement $y$ and generates the command $u_{c}$ .

The weighted design interconnection.

Define the weights and build an LPV model of this interconnection.

% Add input/output names to plant
G.InputName = {'u'; 'f1'; 'f2'};
G.OutputName = 'Gy';

% Actuator model
act = ss(-100,100,1,0);
act.InputName = 'uc';
act.OutputName = 'u';

% Weight: Control Command
Wu = ss(1/50);
Wu.InputName = 'uc';
Wu.OutputName = 'eu';

% Weight: Actuator Output
Wa = ss(0.00001);
Wa.InputName = 'u';
Wa.OutputName = 'ea';

% Weight: Tracking Error
We = tf(2,[1 0.04]);
We.InputName = 'e';
We.OutputName = 'er';

% Weight: Noise
Wn = tf([1,0.4],[0.01 400]);
Wn.InputName = 'dn';
Wn.OutputName = 'n';

% Form synthesis interconnection
sum1 = sumblk('y = Gy + n');
sum2 = sumblk('e = Gy - r');
IC = connect(G,act,Wu,Wa,We,Wn,sum1,sum2,{'r','f1','f2','dn','uc'},...
     {'eu','ea','er','r','y'});

Construct a grid of ( ${Ω_{1}^{2}}_{}$ , $Ω_{2}^{2}$ ) values and compute the $H_{2}$ -optimal controller at each grid point.

p1 = linspace(0,9,3);
p2 = linspace(0,25,3);
[p1,p2] = ndgrid(p1,p2);

Sample IC at grid points and design $H_{2}$ -optimal controllers.

nmeas = 2;   % # of measurements
ncon = 1;    % # of controls
ICs = sample(IC,[],p1,p2);
Ks = ss( zeros([ncon nmeas size(p1)]) );
for i=1:numel(p1)
   Ks(:,:,i) = h2syn(ICs(:,:,i),nmeas,ncon);
end

Use ssInterpolant to create a gain-scheduled controller that linearly interpolates these $H_{2}$ controllers between grid points. This approach is valid when the rotational rates vary slowly. Alternative LPV methods for rapid changes are described in [1].

Ks.SamplingGrid = struct('p1',p1,'p2',p2);
Klpv = ssInterpolant(Ks,[]);
Klpv.InputName = {'r','Gy'};
Klpv.OutputName = {'uc'};

LTI Performance Evaluation

Evaluate the gain-scheduled controller for fixed rotation rates using a finer grid than for the controller design.

Form closed-loop system from [r;f1;f2] to Gy.

CL = connect(G,act,Klpv,{'r','f1','f2'},{'Gy'});

Evaluate open and closed-loop on a finer grid of points.

p1 = linspace(0,9,5);
p2 = linspace(0,25,5);
[p1,p2] = ndgrid(p1,p2);
Gs = sample(G,[],p1,p2);
CLs = sample(CL,[],p1,p2);

The controller achieves good tracking with minimal overshoot, approximately 2.5 s settling time, and less than 3% steady-state tracking error. Furthermore, the disturbances have minimal effect.

step(CLs,5)
grid on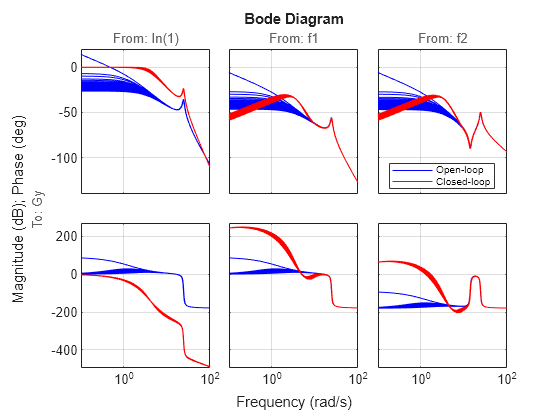

MATLAB figure

The closed-loop Bode response from r to Gy has a DC gain near one with a bandwidth near 3 rad/s. It shows good disturbance attenuation below 1 rad/s compared to the open loop.

bode(Gs,"b",CLs,"r",{0.1,100})
legend("Open-loop","Closed-loop","Location","best")
grid minor

MATLAB figure

LPV Performance Evaluation

Finally, evaluate the gain-scheduled controller with a time-domain simulation with time-varying rotation rates. The parameters vary in time as follows:

$p_{1} (t) = Ω_{1}^{2} (t) = \sin (t) + 1.5$ , $p_{2} (t) = Ω_{2}^{2} (t) = 0.5 \cos (5 t) + 3$ .

The reference signal $r$ is a unit step and the disturbances are set to

$f_{1} (t) = \cos (3 t) + \sin (5 t) + \cos (8 t)$ , $f_{2} (t) = \cos (t) + \sin (2 t) + \cos (4 t)$ .

Define the inputs to the system.

t = 0:0.01:15;
u = ones(size(t));
d1 = cos(3*t)+sin(5*t)+cos(8*t);
d2 = cos(t)+sin(2*t)+cos(4*t);

Define the trajectories of the parameters.

p1 = sin(t)+1.5;
p2 = 0.5*cos(5*t)+3;

Simulate the LPV model with and without disturbances.

[y1,t1,x1] = lsim(CL,[u;d1;d2],t,[],[p1;p2]);
[y2,t2,x2] = lsim(CL,[u;0*d1;0*d2],t,[],[p1;p2]);

figure 
plot(t1,y1,"b",t2,y2,"r");
grid on;
title("LPV Simulation")
ylabel("y");
legend("With disturbances","Without disturbances","Location","best")

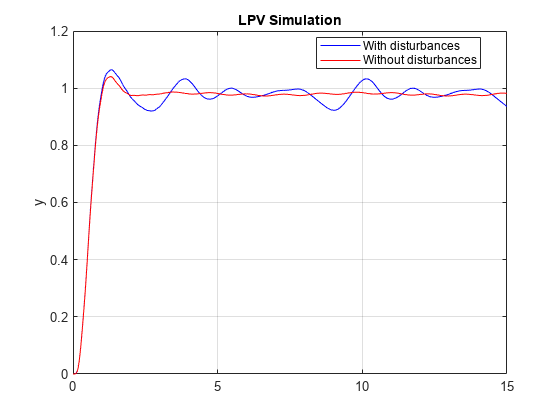
Figure contains an axes object. The axes object with title LPV Simulation, ylabel y contains 2 objects of type line. These objects represent With disturbances, Without disturbances.

The error due to the disturbances is on the order of 5% and consists of 1–2 Hz oscillations about the disturbance-free response. This frequency range is incidentally where the LTI frequency response analysis indicates that disturbances have the greatest impact on the output signal.

Data Function

type disksGFCN.m

function [A,B,C,D,E,dx0,x0,u0,y0,Delays] = GFCN(t,p,m1,m2,k,b)
% Matrices and offsets for LPV model of spinning disks.

% Enforce 0<=p1<=9, 0<=p2<=25
p(1) = max(0,min(p(1),9));
p(2) = max(0,min(p(2),25));

% Define state-space matrices
A = [   0              0            1       0    ; ...
        0              0            0       1    ; ...
    p(1)-k/m1       -k/m1        -b/m1     0    ; ...
      -k/m2         p(2)-k/m2       0     -b/m2  ];
B = [    0      0       0     ; ...
         0      0       0     ; ...
      1/m1   .1/m1      0     ; ...  
         0      0     .1/m2 ];
C = [ 0 1 0 0];
D = [0 0 0];
E = [];
% no offsets or delays
dx0 = []; x0 = []; u0 = []; y0 = []; Delays = [];

References

[1] Wu, Fen. "Control of Linear Parameter Varying Systems," Ph.D. dissertation, Department of Mechanical Engineering, University of California at Berkeley, May 1995.