卡尔曼滤波

打开实时脚本

此示例说明如何执行卡尔曼滤波。首先，使用 kalman 命令设计一个稳态滤波器。然后，对系统进行仿真以显示它如何降低测量噪声带来的误差。此示例还说明如何实现一个时变滤波器，这对于具有非平稳噪声源的系统非常有用。

稳态卡尔曼滤波器

假设有以下输入端为高斯噪声 w、输出端为测量噪声 v 的离散被控对象：

$\begin{array}{c} x [n + 1] = A x [n] + B u [n] + G w [n] \\ y [n] = C x [n] + D u [n] + H w [n] + v [n] \end{array}$

目标是设计一个卡尔曼滤波器，根据含噪测量值 $y [n]$ 来估计真实的被控对象输出 $y_{t} [n] = y [n] - v [n]$ 。这种稳态卡尔曼滤波器使用以下方程进行这种估计。

时间更新：

$\hat{x} [n + 1 | n] = A \hat{x} [n | n - 1] + Bu [n] + Gw [n]$

测量更新：

$\begin{array}{l} x_{}^{ˆ} [n | n] = x_{}^{ˆ} [n | n - 1] + M_{x} (y [n] - C x_{}^{ˆ} [n | n - 1] - D u [n]) \\ y_{}^{ˆ} [n | n] = C x_{}^{ˆ} [n | n - 1] + D u [n] + M_{y} (y [n] - C x_{}^{ˆ} [n | n - 1] - D u [n]) \end{array}$

其中，

$\hat{x} [n | n - 1]$ 基于给定的到 $y [n - 1]$ 为止的过往测量值计算的 $x [n]$ 的估计值。
$\hat{x} [n | n]$ 和 $\hat{y} [n | n]$ 是估计的状态值和测量值，它们基于上一次测量值 $y [n]$ 进行更新。
$M_{x}$ 和 $M_{y}$ 是最优新信息增益，在给定噪声协方差 $E (w [n] {w [n]}^{T}) = Q$ 、 $E (v [n] {v [n]}^{T}) = R$ 和 $N = E (w [n] {v [n]}^{T}) = 0$ 的情况下，通过最小化估计误差的稳态协方差来选择最优值。（有关如何选择这些增益的详细信息，请参阅kalman。）

（这些更新方程描述一个 current 类型估计器。有关 current 估计器和 delayed 估计器之间差异的信息，请参阅kalman。）

设计滤波器

您可以使用 kalman 函数来设计此稳态卡尔曼滤波器。此函数根据您提供的过程噪声协方差 Q 和传感器噪声协方差 R 确定特定被控对象的最佳稳态滤波器增益 M。对于此示例，使用以下值作为被控对象的状态空间矩阵。

A = [1.1269   -0.4940    0.1129 
     1.0000         0         0 
          0    1.0000         0];

B = [-0.3832
      0.5919
      0.5191];

C = [1 0 0];

D = 0;

对于此示例，设置 $G = B$ ，意味着过程噪声 w 是加性输入噪声。此外，设置 $H = 0$ ，意味着输入噪声 w 对输出 y 没有直接影响。这些假设产生更简单的被控对象模型：

$\begin{array}{c} x [n + 1] = A x [n] + B u [n] + B w [n] \\ y [n] = C x [n] + v [n] \end{array}$

当 H = 0 时，可以证明 $M_{y} = C M_{x}$ （请参阅kalman）。总的来说，这些假设也简化了卡尔曼滤波器的更新方程。

时间更新：

$\hat{x} [n + 1 | n] = A \hat{x} [n | n - 1] + Bu [n] + Bw [n]$

测量更新：

$\begin{array}{l} x_{}^{ˆ} [n | n] = x_{}^{ˆ} [n | n - 1] + M_{x} (y [n] - C x_{}^{ˆ} [n | n - 1]) \\ y_{}^{ˆ} [n | n] = C x_{}^{ˆ} [n | n] \end{array}$

要设计此滤波器，首先创建具有 w 的一个输入的被控对象模型。将采样时间设置为 -1 以将被控对象标记为离散（没有特定采样时间）。

Ts = -1;
sys = ss(A,[B B],C,D,Ts,'InputName',{'u' 'w'},'OutputName','y');  % Plant dynamics and additive input noise w

过程噪声协方差 Q 和传感器噪声协方差 R 是大于零的值，通常从对系统的研究或测量值中获得。对于此示例，请指定以下值。

Q = 2.3; 
R = 1;

使用 kalman 命令设计滤波器。

[kalmf,L,~,Mx,Z] = kalman(sys,Q,R);

此命令设计卡尔曼滤波器 kalmf，这是实现时间更新和测量更新方程的状态空间模型。滤波器输入是被控对象输入 u 和含噪被控对象输出 y。kalmf 的第一个输出是真实被控对象输出的估计值 $\hat{y}$ ，其余输出是状态估计值 $\hat{x}$ 。

对于此示例，丢弃状态估计值，只保留第一个输出 $\hat{y}$ 。

kalmf = kalmf(1,:);

使用滤波器

要了解此滤波器的工作原理，请生成一些数据，并将滤波后的响应与真实的被控对象响应进行比较。完整的系统如下图所示。

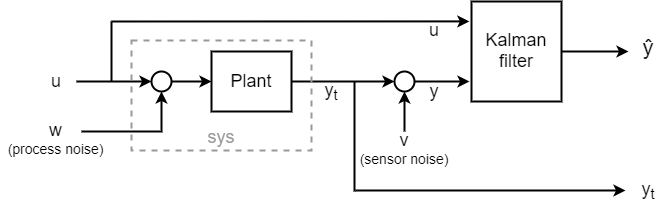
要仿真此系统，请使用 sumblk 为测量噪声 v 创建一个输入。然后，使用 connect 将 sys 和卡尔曼滤波器联接在一起，使得 u 是共享输入，并且含噪被控对象输出 y 馈入另一个滤波器输入。其结果是一个仿真模型，它具有输入 w、v 和 u，输出 yt（真实响应）和 ye（经过滤波的响应或估计的响应 $\hat{y}$ ）。信号 yt 和 ye 分别是被控对象和滤波器的输出。

sys.InputName = {'u','w'};
sys.OutputName = {'yt'};
vIn = sumblk('y=yt+v');

kalmf.InputName = {'u','y'};
kalmf.OutputName = 'ye';

SimModel = connect(sys,vIn,kalmf,{'u','w','v'},{'yt','ye'});

要模拟滤波器行为，需要生成一个已知正弦输入向量。

t = (0:100)';
u = sin(t/5);

使用设计滤波器时使用的相同噪声协方差值 Q 和 R 生成过程噪声和传感器含噪向量。

rng(10,'twister');
w = sqrt(Q)*randn(length(t),1);
v = sqrt(R)*randn(length(t),1);

最后，使用 lsim 仿真响应。

out = lsim(SimModel,[u,w,v]);

lsim 在输出端 yt 和 ye 生成对 w、v 和 u 输入的响应。提取 yt 和 ye 通道，并计算测量的响应。

yt = out(:,1);   % true response
ye = out(:,2);  % filtered response
y = yt + v;     % measured response

将真实响应与滤波后的响应进行比较。

clf
subplot(211), plot(t,yt,'b',t,ye,'r--'), 
xlabel('Number of Samples'), ylabel('Output')
title('Kalman Filter Response')
legend('True','Filtered')
subplot(212), plot(t,yt-y,'g',t,yt-ye,'r--'),
xlabel('Number of Samples'), ylabel('Error')
legend('True - measured','True - filtered')

Figure contains 2 axes objects. Axes object 1 with title Kalman Filter Response, xlabel Number of Samples, ylabel Output contains 2 objects of type line. These objects represent True, Filtered. Axes object 2 with xlabel Number of Samples, ylabel Error contains 2 objects of type line. These objects represent True - measured, True - filtered.

如第二个图所示，卡尔曼滤波器能够减少由于测量噪声引起的误差 yt - y。要确认这种误差减少，请计算滤波前的误差协方差（测量误差协方差）和滤波后的误差协方差（估计误差协方差）。

MeasErr = yt - y;
MeasErrCov = sum(MeasErr.*MeasErr)/length(MeasErr)

MeasErrCov = 
0.9871

EstErr = yt - ye;
EstErrCov = sum(EstErr.*EstErr)/length(EstErr)

EstErrCov = 
0.3479

时变卡尔曼滤波器设计

之前的设计假设噪声协方差不随时间而改变。即使在噪声协方差不平稳时，时变卡尔曼滤波器也能很好地工作。

时变卡尔曼滤波器具有以下更新方程。在时变滤波器中，误差协方差 $P [n]$ 和新信息增益 $M_{x} [n]$ 都可以随时间而改变。您可以修改时间和测量更新方程以考虑时变，如下所示，再次采用 $G = B$ ，因此过程噪声 w 是加性输入噪声。

时间更新：

$\begin{array}{l} x_{}^{ˆ} [n + 1 | n] = A x_{}^{ˆ} [n | n] + B u [n] + B w [n] \\ P [n + 1 | n] = A P [n | n] A^{T} + B Q B^{T} \end{array}$

测量更新：

$\begin{array}{l} x_{}^{ˆ} [n | n] = x_{}^{ˆ} [n | n - 1] + M_{x} [n] (y [n] - C x_{}^{ˆ} [n | n - 1]) \\ M_{x} [n] = P [n | n - 1] C^{T} {(C P [n | n - 1] C^{T} + R [n])}^{- 1} \\ P [n | n] = (I - M_{x} [n] C) P [n | n - 1] \\ y_{}^{ˆ} [n | n] = C x_{}^{ˆ} [n | n] \end{array}$

有关这些表达式的详细信息，请参阅kalman。

在 Simulink® 中，您可以使用 Kalman Filter 模块（请参阅State Estimation Using Time-Varying Kalman Filter）实现时变卡尔曼滤波器。

要在 MATLAB® 中创建时变卡尔曼滤波器，请首先生成含噪被控对象响应。仿真被控对象对之前定义的输入信号 u 和过程噪声 w 的响应。然后，将测量噪声 v 与仿真的真实响应 yt 相加以获得含噪响应 y。在此示例中，含噪向量 w 和 v 的协方差不随时间而变化。但是，您可以对非平稳噪声使用相同的过程。

yt = lsim(sys,[u w]);   
y = yt + v;

接下来，在 for 循环中实现递归滤波器更新方程。

P = B*Q*B';         % Initial error covariance
x = zeros(3,1);     % Initial condition on the state

ye = zeros(length(t),1);
ycov = zeros(length(t),1); 
errcov = zeros(length(t),1); 

for i=1:length(t)
  % Measurement update
  Mxn = P*C'/(C*P*C'+R);
  x = x + Mxn*(y(i)-C*x);   % x[n|n]
  P = (eye(3)-Mxn*C)*P;     % P[n|n]

  ye(i) = C*x;
  errcov(i) = C*P*C';

  % Time update
  x = A*x + B*u(i);        % x[n+1|n]
  P = A*P*A' + B*Q*B';     % P[n+1|n] 
end

将真实响应与滤波后的响应进行比较。

subplot(211), plot(t,yt,'b',t,ye,'r--')
xlabel('Number of Samples'), ylabel('Output')
title('Response with Time-Varying Kalman Filter')
legend('True','Filtered')
subplot(212), plot(t,yt-y,'g',t,yt-ye,'r--'),
xlabel('Number of Samples'), ylabel('Error')
legend('True - measured','True - filtered')

Figure contains 2 axes objects. Axes object 1 with title Response with Time-Varying Kalman Filter, xlabel Number of Samples, ylabel Output contains 2 objects of type line. These objects represent True, Filtered. Axes object 2 with xlabel Number of Samples, ylabel Error contains 2 objects of type line. These objects represent True - measured, True - filtered.

时变滤波器还会在估计期间估计输出协方差。由于此示例使用平稳输入噪声，输出协方差趋于稳态值。绘制输出协方差图以确认滤波器已达到稳态。

figure
plot(t,errcov) 
xlabel('Number of Samples'), ylabel('Error Covariance'),

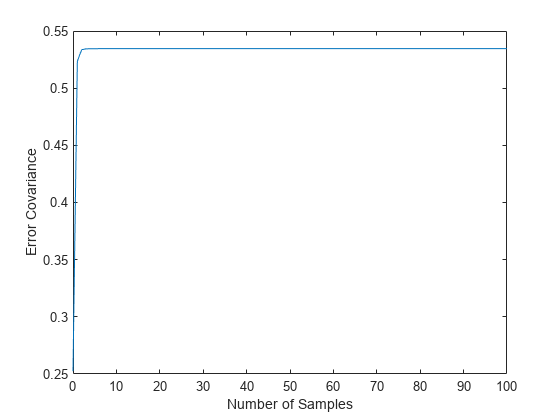
Figure contains an axes object. The axes object with xlabel Number of Samples, ylabel Error Covariance contains an object of type line.

从协方差图可以看出，输出协方差在大约五个采样后达到稳态。从那时起，时变滤波器具有与稳态版本相同的性能。

与稳态情况一样，滤波器降低了测量噪声引起的误差。要确认这种误差减少，请计算滤波前的误差协方差（测量误差协方差）和滤波后的误差协方差（估计误差协方差）。

MeasErr = yt - y;
MeasErrCov = sum(MeasErr.*MeasErr)/length(MeasErr)

MeasErrCov = 
0.9871

EstErr = yt - ye;
EstErrCov = sum(EstErr.*EstErr)/length(EstErr)

EstErrCov = 
0.3479

最后，当时变滤波器达到稳态时，增益矩阵 Mxn 中的值与 kalman 为稳态滤波器计算的值匹配。

Mx,Mxn

Mxn = 3×1

    0.5345
    0.0101
   -0.4776

有关卡尔曼滤波器的详细信息

有关卡尔曼滤波器的详细信息，请播放以下视频，或观看了解卡尔曼滤波器 - MATLAB 技术讲座上提供的其余系列视频。

另请参阅

kalman

主题

外部网站

了解卡尔曼滤波器 - MATLAB 系列视频

卡尔曼滤波

稳态卡尔曼滤波器

设计滤波器

使用滤波器

时变卡尔曼滤波器设计

有关卡尔曼滤波器的详细信息

视频脚本

另请参阅

主题

外部网站