MIMO 状态空间模型
MIMO 显式状态空间模型
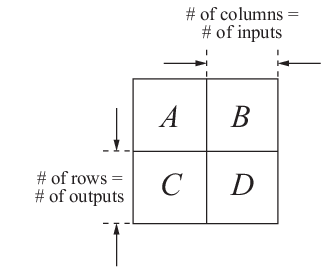
创建 MIMO 状态空间模型的方法与创建 SISO 状态空间模型相同。SISO 和 MIMO 之间的唯一区别在于状态空间矩阵的维度。B、C 和 D 矩阵的维度随输入和输出数量的增加而增加,如下图所示。
在此示例中,您为具有惯性张量 J、阻尼力 F 和三个旋转轴的旋转体创建状态空间模型,其关系为:
系统输入 T 为驱动扭矩。输出 y 为旋转体的角速度向量。
要将此系统表示为状态空间形式:
将其重写为:
那么状态空间矩阵为:
要创建此模型,请输入以下命令:
J = [8 -3 -3; -3 8 -3; -3 -3 8]; F = 0.2*eye(3); A = -J\F; B = inv(J); C = eye(3); D = 0; sys_mimo = ss(A,B,C,D);
这些命令假设 J 是绕顶点旋转的立方体的惯性张量,阻尼力幅值为 0.2。
sys_mimo 是 ss 模型。
MIMO 描述符形式的状态空间模型
此示例说明如何使用 dss 创建连续时间描述符形式的(隐式)状态空间模型。
此示例使用 MIMO 显式状态空间模型中所示的同一旋转体系统。在此示例中,通过对惯性矩阵 J 求逆得到 B 矩阵的值。如果 J 的求逆条件数较差,可改用描述符形式的(隐式)状态空间模型。描述符形式的(隐式)状态空间模型的形式如下:
为具有惯性张量 J、阻尼力 F 和三个旋转轴的旋转体创建状态空间模型,其关系为:
系统输入 T 为驱动扭矩。输出 y 为旋转体的角速度向量。您可以将此系统写为具有以下状态空间矩阵的描述符形式的状态空间模型:
要创建此系统,请输入:
J = [8 -3 -3; -3 8 -3; -3 -3 8]; F = 0.2*eye(3); A = -F; B = eye(3); C = eye(3); D = 0; E = J; sys_mimo = dss(A,B,C,D,E)
这些命令假设 J 是绕顶点旋转的立方体的惯性张量,阻尼力幅值为 0.2。
sys 是一个 ss 模型,且具有非空 E 矩阵。
喷气式运输机的状态空间模型
此示例说明如何构建喷气式运输机的 MIMO 模型。由于喷气式飞机物理模型开发的内容繁多,此处只介绍其中的状态空间方程。有关飞机飞行的物理学原理的更完整讨论,请参阅标准的航空教科书。
巡航飞行时 MACH = 0.8 且 H = 40,000 英尺状态下喷气式飞机模型如下
A = [-0.0558 -0.9968 0.0802 0.0415
0.5980 -0.1150 -0.0318 0
-3.0500 0.3880 -0.4650 0
0 0.0805 1.0000 0];
B = [ 0.0073 0
-0.4750 0.0077
0.1530 0.1430
0 0];
C = [0 1 0 0
0 0 0 1];
D = [0 0
0 0];
使用以下命令将此状态空间模型指定为 LTI 对象,并将名称附加到状态、输入和输出。
states = {'beta' 'yaw' 'roll' 'phi'};
inputs = {'rudder' 'aileron'};
outputs = {'yaw rate' 'bank angle'};
sys_mimo = ss(A,B,C,D,'statename',states,...
'inputname',inputs,...
'outputname',outputs);
您可以通过键入 sys_mimo 来显示 LTI 模型。
sys_mimo
a =
beta yaw roll phi
beta -0.0558 -0.9968 0.0802 0.0415
yaw 0.598 -0.115 -0.0318 0
roll -3.05 0.388 -0.465 0
phi 0 0.0805 1 0
b =
rudder aileron
beta 0.0073 0
yaw -0.475 0.0077
roll 0.153 0.143
phi 0 0
c =
beta yaw roll phi
yaw rate 0 1 0 0
bank angle 0 0 0 1
d =
rudder aileron
yaw rate 0 0
bank angle 0 0
Continuous-time model.
该模型有两个输入和两个输出。beta(侧滑角)和 phi(倾斜角)的单位为弧度;yaw(偏航角速度)和 roll(滚转角速度)的单位为弧度/秒。方向舵和副翼偏转以度为单位。
与在 SISO 示例中一样,我们使用 tf 来推导传递函数表示。
tf(sys_mimo)
Transfer function from input "rudder" to output...
-0.475 s^3 - 0.2479 s^2 - 0.1187 s - 0.05633
yaw rate: ---------------------------------------------------
s^4 + 0.6358 s^3 + 0.9389 s^2 + 0.5116 s + 0.003674
0.1148 s^2 - 0.2004 s - 1.373
bank angle: ---------------------------------------------------
s^4 + 0.6358 s^3 + 0.9389 s^2 + 0.5116 s + 0.003674
Transfer function from input "aileron" to output...
0.0077 s^3 - 0.0005372 s^2 + 0.008688 s + 0.004523
yaw rate: ---------------------------------------------------
s^4 + 0.6358 s^3 + 0.9389 s^2 + 0.5116 s + 0.003674
0.1436 s^2 + 0.02737 s + 0.1104
bank angle: ---------------------------------------------------
s^4 + 0.6358 s^3 + 0.9389 s^2 + 0.5116 s + 0.003674