Nichols Plot Design
Nichols plot design is an interactive graphical method of modifying a compensator to
achieve a specific open-loop response (loop shaping). Unlike Bode Diagram Design, Nichols plot design uses Nichols plots to view the
open-loop frequency response. Nichols plots combine gain and phase information into a
single plot, which is useful when you are designing to gain and phase margin
specifications. For more information on Nichols plots, see nicholsplot.
Tune Compensator for DC Motor Using Nichols Plot Graphical Design
This example shows how to design a compensator for a DC motor using Nichols plot graphical tuning techniques.
Plant Model and Requirements
The transfer function of the DC motor plant, as described in SISO Example: The DC Motor, is:
For this example, the design requirements are:
Rise time of less than 0.5 seconds
Steady-state error of less than 5%
Overshoot of less than 10%
Gain margin greater than 20 dB
Phase margin greater than 40 degrees
Open Control System Designer
At the MATLAB® command line, create a transfer function model of the plant, and open Control System Designer in the Nichols Editor configuration.
G = tf(1.5,[1 14 40.02]);
controlSystemDesigner('nichols',G);The app opens and imports G as the plant model for the
default control architecture, Configuration 1.
In the app, the following response plots open:
Open-loop Nichols Editor for the
LoopTransfer_Cresponse. This response is the open-loop transfer function GC, where C is the compensator and G is the plant.Step Response for the
IOTransfer_r2yresponse. This response is the input-output transfer function for the overall closed-loop system.
Tip
To open the open-loop Nichols Editor when
Control System Designer is already open, on the
Control System tab, in the Tuning
Methods drop-down list, select Nichols
Editor. In the Select Response to Edit dialog box, select
an existing response to plot, or create a New Open-Loop
Response.
The app displays the Nichols Editor and Step Response plots side-by-side.
Adjust Bandwidth
Since the design requires a rise time less than 0.5 seconds, set the open-loop DC crossover frequency to about 3 rad/s. To a first-order approximation, this crossover frequency corresponds to a time constant of 0.33 seconds.
To adjust the crossover frequency increase the compensator gain. In the Nichols Editor, drag the response upward. Doing so increases the gain of the compensator.
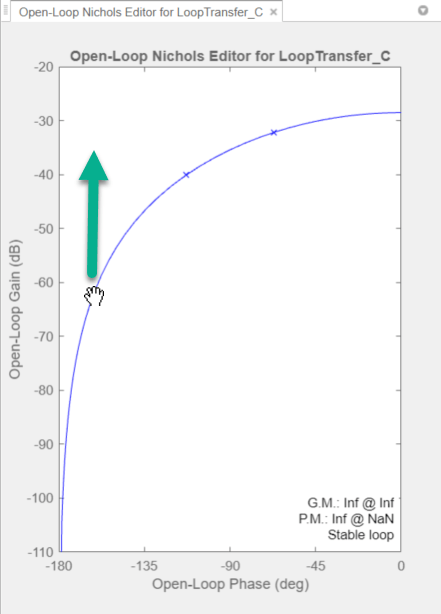
As you drag the Nichols plot, the app computes the compensator gain and updates the response plots.
Drag the Nichols plot upward until the crossover frequency is about 3 rad/s.
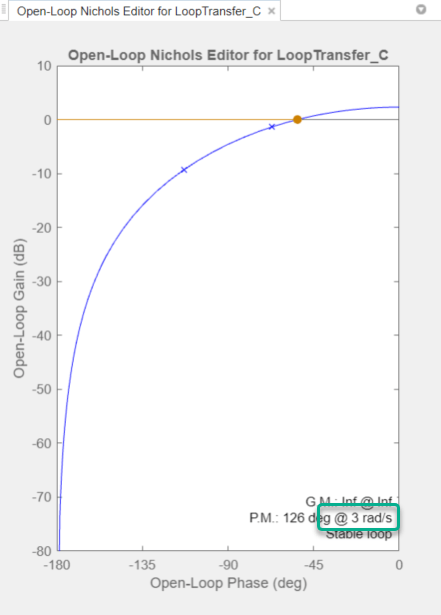
View Step Response Characteristics
To add the rise time to the Step Response plot, right-click the plot area, and select Characteristics > Rise Time.
To view the rise time, move the cursor over the rise time indicator.

The rise time is around 0.23 seconds, which satisfies the design requirements.
Similarly, to add the peak response to the Step Response plot, right-click the plot area, and select Characteristics > Peak Response.

The peak overshoot is around 3.5%.
Add Integrator to Compensator
To meet the 5% steady-state error requirement, eliminate steady-state error from the closed-loop step response by adding an integrator to your compensator. In the Nichols Editor right-click in the plot area, and select Add Pole or Zero > Integrator.

Adding an integrator produces zero steady-state error. However, changing the compensator dynamics also changes the crossover frequency, increasing the rise time. To reduce the rise time, increase the crossover frequency to around 3 rad/s.
Adjust Compensator Gain
To return the crossover frequency to around 3 rad/s, increase the compensator gain further. Right-click the Nichols Editor plot area, and select Edit Compensator.
In the Compensator Editor dialog box, in the
Compensator section, specify a gain of
99, and press Enter.
The response plots update automatically.
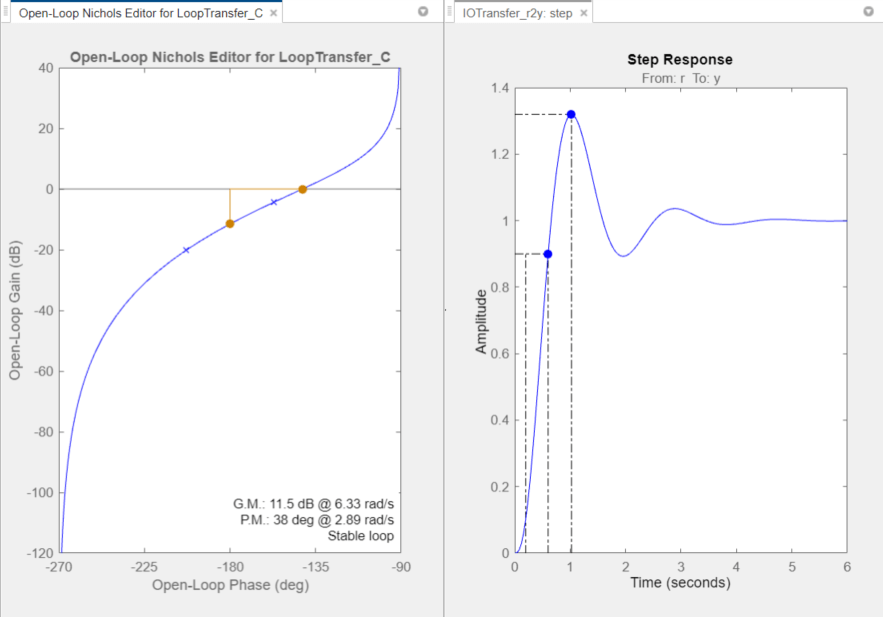
The rise time is around 0.4 seconds, which satisfies the design requirements. However, the peak overshoot is around 32%. A compensator consisting of a gain and an integrator is not sufficient to meet the design requirements. Therefore, the compensator requires additional dynamics.
Add Lead Network to Compensator
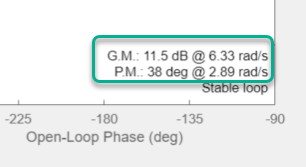
In the Nichols Editor, review the gain margin and phase margin for the current compensator design. The design requires a gain margin greater than 20 dB and phase margin greater than 40 degrees. The current design does not meet either of these requirements.
To increase the stability margins, add a lead network to the compensator.
In the Nichols Editor, right-click and select Add Pole or Zero > Lead.
To specify the location of the lead network pole, click on the magnitude
response. The app adds a real pole (red X) and real zero
(red O) to the compensator and to the Nichols
Editor plot.
In the Nichols Editor, drag the pole and zero to change their locations. As you drag them, the app updates the pole/zero values and updates the response plots.
To decrease the magnitude of a pole or zero, drag it towards the left. Since the pole and zero are on the negative real axis, dragging them to the left moves them closer to the origin in the complex plane.
Tip
As you drag a pole or zero, the app displays the new value in the status bar, on the right side.

As an initial estimate, drag the zero to a location around
-7 and the pole to a location around
-11.
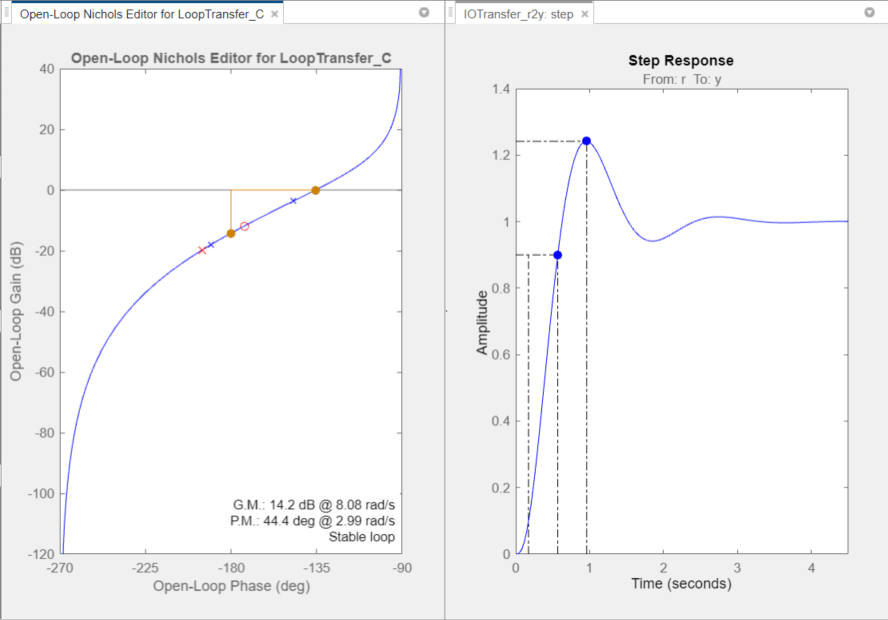
The phase margin meets the design requirements; however, the gain margin is still too low.
Edit Lead Network Pole and Zero
To improve the controller performance, tune the lead network parameters.
In the Compensator Editor dialog box, in the Dynamics section, click the Lead row.
In the Edit Selected Dynamics section, in the
Real Zero text box, specify a location of
-4.3, and press Enter. This value is
near the slowest (left-most) pole of the DC motor plant.
In the Real Pole text box, specify a value of
-28, and press Enter.

When you modify a lead network parameters, the Compensator and response plots update automatically.
In the app, in the Nichols Editor, the gain margin of
20.5 just meets the design requirement.
To add robustness to the system, in the Compensator Editor dialog box,
decrease the compensator gain to 84.5, and press
Enter. The gain margin increases to
21.8, and the response plots update.

In Control System Designer, in the response plots, compare the system performance to the design requirements. The system performance characteristics are:
Rise time is 0.445 seconds.
Steady-state error is zero.
Overshoot is 3.39%.
Gain margin is 21.8 dB.
Phase margin is 65.6 degrees.
The system response meets all of the design requirements.
See Also
Control System Designer | nicholsplot