绘制系统响应

时间响应

创建一个线性系统。对于此示例，请创建一个三阶传递函数。

sys = tf([8 18 32],[1 6 14 24])

sys =
 
     8 s^2 + 18 s + 32
  -----------------------
  s^3 + 6 s^2 + 14 s + 24
 
Continuous-time transfer function.
Model Properties

您可以使用 step 和 impulse 命令分别绘制该系统的阶跃响应和冲激响应。

subplot(2,1,1)
step(sys)
subplot(2,1,2)
impulse(sys)

您还可以使用 lsim 命令对任意信号（例如正弦波）的响应进行仿真。输入信号以灰色显示，系统响应以蓝色显示。

figure
t = 0:0.01:4;
u = sin(10*t);
lsim(sys,u,t)   % u,t define the input signal

您可以将绘图命令用于连续或离散 tf、ss 或 zpk 模型。对于状态空间模型，您还可以绘制从某个给定初始状态开始的非强迫响应。例如：

A = [-0.8 3.6 -2.1;-3 -1.2 4.8;3 -4.3 -1.1];
B = [0; -1.1; -0.2];
C = [1.2 0 0.6];
D = -0.6;
G = ss(A,B,C,D);
x0 = [-1;0;2];  % initial state
initial(G,x0)
grid

频率响应

频域分析是理解控制系统稳定性和性能属性的关键。波特图、奈奎斯特图和尼柯尔斯图是绘制和分析线性系统频率响应的三种标准方法。您可以使用 bode、nichols 和 nyquist 命令创建这些图。

创建一个线性系统。

sys = tf([8 18 32],[1 6 14 24])

sys =
 
     8 s^2 + 18 s + 32
  -----------------------
  s^3 + 6 s^2 + 14 s + 24
 
Continuous-time transfer function.
Model Properties

为该系统创建波特图。

bode(sys)
grid

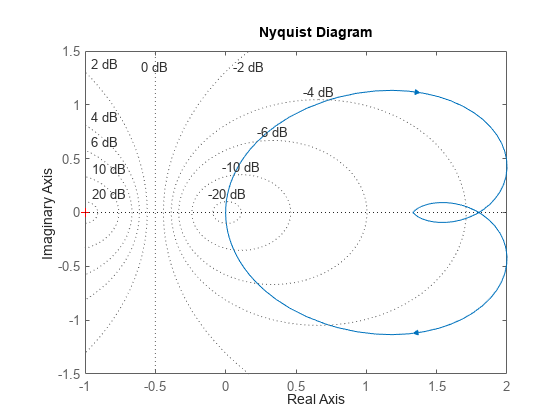
为该系统创建奈奎斯特图。

nyquist(sys)
grid

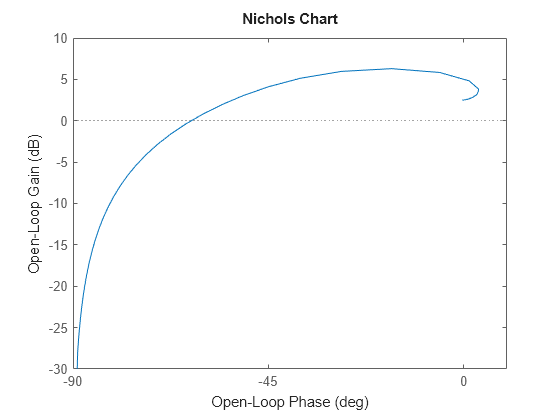
为该系统创建尼柯尔斯图。

nichols(sys)
grid

极点/零点图和根轨迹

系统的极点和零点包含有关其动态特性、稳定性和性能极限的宝贵信息。例如，以如下 SISO 控制环中的反馈环为例。

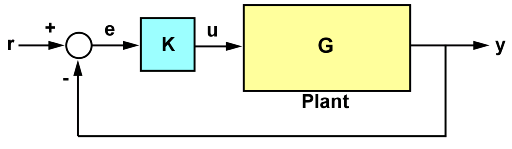
其中：

对于增益值 k = 0.7，您可以使用 pzmap 绘制闭环极点和零点。

s = tf('s');
G = -(2*s+1)/(s^2+3*s+2);
k = 0.7;
T = feedback(G*k,1);
pzmap(T)
grid
axis([-2 0 -1 1])

闭环极点（用蓝色 x 标记）位于左半平面中，因此对于此所选增益 k，反馈环是稳定的。您可以从该图中读取闭环极点的阻尼比（参见径向线上的标签）。此处阻尼比约为 0.7，表明闭环响应具有良好的阻尼特性，如下图所示：

figure
step(T)

为了进一步了解环路增益 k 如何影响闭环稳定性，您可以绘制闭环极点随 k 变化的轨迹。

rlocus(G)
grid

点击轨迹与 y 轴的交点可以发现，当 k = 1.51 时，闭环极点变得不稳定。因此，为确保闭环稳定性，环路增益应保持小于 1.5。

响应特征

右键点击响应图可以访问各种选项和注解。具体而言，特征菜单可显示标准度量，例如阶跃响应的上升时间和稳定时间，或频率响应图的峰值增益和稳定裕度。

使用上一节中的示例，绘制闭环阶跃响应：

step(T)

现在，右键点击该图以显示峰值响应和稳定时间特征，然后点击蓝色圆点以读取相应的超调和稳定时间值：

分析 MIMO 系统

到目前为止提到的所有命令都完全支持多输入多输出 (MIMO) 系统。在 MIMO 系统中，这些命令会生成图数组。例如，假设有以下双输入、双输出系统。

sys = rss(3,2,2);
sys.A = [-0.5 -0.3 -0.2 ; 0 -1.3  -1.7; 0.4 1.7 -1.3];

阶跃响应是一个 2×2 的图数组，其中每一列显示特定输入通道的阶跃响应。

step(sys)

您可以通过右键点击该图并选择 I/O 分组 -> 全部子菜单，将所有四个响应组合到单个图中。

以下附加图对于分析 MIMO 系统非常有用：

例如，绘制 sys 的峰值增益随频率变化的图：

sigma(sys)
grid

比较系统

您可以使用任何响应图命令同时绘制多个系统。您可以赋给每个系统特定的颜色、标记或线型，以便于比较。使用上面的反馈示例，用三种不同的颜色绘制环路增益 k 的三个值对应的闭环阶跃响应：

k1 = 0.4;
T1 = feedback(G*k1,1);
k2 = 1;
T2 = feedback(G*k2,1);
step(T,'b',T1,'r',T2,'g')
legend('k = 0.7','k = 0.4','k = 1');

修改时间轴值或频率轴值

您可以修改现有线性分析图的时间向量和频率向量。

对于 step 和 impulse 图，您可以通过右键点击绘图区域并选择指定时间来指定时间向量。

在“指定时间”对话框中，您可以使用以下方法之一定义时间值和单位。

对于 bode、nyquist、nichols 和 sigma 图，您可以通过右键点击绘图区域并选择指定频率来指定频率向量。

在“指定频率”对话框中，您可以使用以下方法之一定义频率值和单位。

如果您的系统是 frd 对象，则绘图会在频率值之间对响应进行插值。

通过更改时间和频率单位可以指定输入的单位，但不会更改绘图中的单位。