评估曲面拟合
此示例说明如何使用曲面拟合。
加载数据并拟合多项式曲面
load franke; surffit = fit([x,y],z,'poly23','normalize','on')
surffit =
Linear model Poly23:
surffit(x,y) = p00 + p10*x + p01*y + p20*x^2 + p11*x*y + p02*y^2 + p21*x^2*y
+ p12*x*y^2 + p03*y^3
where x is normalized by mean 1982 and std 868.6
and where y is normalized by mean 0.4972 and std 0.2897
Coefficients (with 95% confidence bounds):
p00 = 0.4253 (0.3928, 0.4578)
p10 = -0.106 (-0.1322, -0.07974)
p01 = -0.4299 (-0.4775, -0.3822)
p20 = 0.02104 (0.001457, 0.04062)
p11 = 0.07153 (0.05409, 0.08898)
p02 = -0.03084 (-0.05039, -0.01129)
p21 = 0.02091 (0.001372, 0.04044)
p12 = -0.0321 (-0.05164, -0.01255)
p03 = 0.1216 (0.09929, 0.1439)
输出显示拟合的模型方程、拟合的系数以及拟合系数的置信边界。
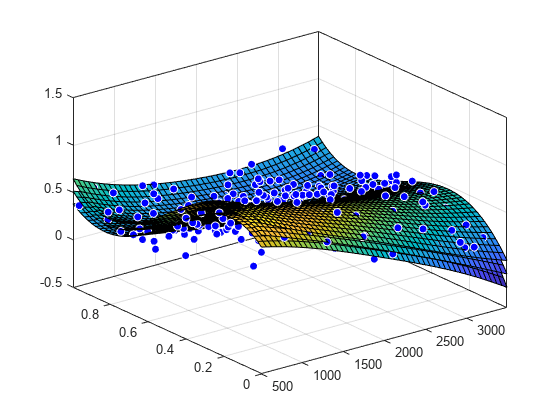
绘制拟合、数据、残差和预测边界
plot(surffit,[x,y],z)

绘制残差拟合图。
plot(surffit,[x,y],z,'Style','Residuals')

绘制拟合的预测边界。
plot(surffit,[x,y],z,'Style','predfunc')
评估指定点处的拟合
使用以下形式通过指定 x 和 y 的值来计算特定点处的拟合值:z = fittedmodel(x,y)。
surffit(1000,0.5)
ans = 0.5673
评估多个点处的拟合值
xi = [500;1000;1200]; yi = [0.7;0.6;0.5]; surffit(xi,yi)
ans = 3×1
0.3771
0.4064
0.5331
获取这些值的预测边界。
[ci, zi] = predint(surffit,[xi,yi])
ci = 3×2
0.0713 0.6829
0.1058 0.7069
0.2333 0.8330
zi = 3×1
0.3771
0.4064
0.5331
获取模型方程
输入拟合名称以显示模型方程、拟合系数和拟合系数的置信边界。
surffit
surffit =
Linear model Poly23:
surffit(x,y) = p00 + p10*x + p01*y + p20*x^2 + p11*x*y + p02*y^2 + p21*x^2*y
+ p12*x*y^2 + p03*y^3
where x is normalized by mean 1982 and std 868.6
and where y is normalized by mean 0.4972 and std 0.2897
Coefficients (with 95% confidence bounds):
p00 = 0.4253 (0.3928, 0.4578)
p10 = -0.106 (-0.1322, -0.07974)
p01 = -0.4299 (-0.4775, -0.3822)
p20 = 0.02104 (0.001457, 0.04062)
p11 = 0.07153 (0.05409, 0.08898)
p02 = -0.03084 (-0.05039, -0.01129)
p21 = 0.02091 (0.001372, 0.04044)
p12 = -0.0321 (-0.05164, -0.01255)
p03 = 0.1216 (0.09929, 0.1439)
要仅获得模型方程,请使用 formula。
formula(surffit)
ans = 'p00 + p10*x + p01*y + p20*x^2 + p11*x*y + p02*y^2 + p21*x^2*y + p12*x*y^2 + p03*y^3'
获取系数名称和值
通过名称指定一个系数。
p00 = surffit.p00
p00 = 0.4253
p03 = surffit.p03
p03 = 0.1216
获取所有系数名称。查看拟合方程(例如 f(x,y) = p00 + p10*x...)以查看每个系数的模型项。
coeffnames(surffit)
ans = 9×1 cell
{'p00'}
{'p10'}
{'p01'}
{'p20'}
{'p11'}
{'p02'}
{'p21'}
{'p12'}
{'p03'}
获取所有系数值。
coeffvalues(surffit)
ans = 1×9
0.4253 -0.1060 -0.4299 0.0210 0.0715 -0.0308 0.0209 -0.0321 0.1216
获得系数的置信边界
使用系数的置信边界来帮助您评估和比较拟合情况。系数的置信边界确定其准确性。相距很远的边界表示存在不确定性。如果线性系数的置信边界跨越了零点,这意味着您无法确定这些系数是否与零有差异。如果一些模型项的系数为零,则它们对拟合没有影响。
confint(surffit)
ans = 2×9
0.3928 -0.1322 -0.4775 0.0015 0.0541 -0.0504 0.0014 -0.0516 0.0993
0.4578 -0.0797 -0.3822 0.0406 0.0890 -0.0113 0.0404 -0.0126 0.1439
查找方法
列出您可以用于拟合的每种方法。
methods(surffit)
Methods for class sfit: argnames category coeffnames coeffvalues confint dependnames differentiate feval fitoptions formula indepnames islinear numargs numcoeffs plot predint probnames probvalues quad2d setoptions sfit type
有关如何使用拟合方法的详细信息,请参阅 sfit。