前馈和循环神经网络

动态网络可以分为两类：只有前馈连接的网络，以及具有反馈连接或循环连接的网络。要了解静态网络、前馈动态网络和循环动态网络之间的差异，请创建一些网络并观察它们如何响应输入序列。（首先，您可能要查看在动态网络中使用顺序输入进行仿真。）

使用以下命令创建一个脉冲输入序列并进行绘图：

p = {0 0 1 1 1 1 0 0 0 0 0 0};
stem(cell2mat(p))

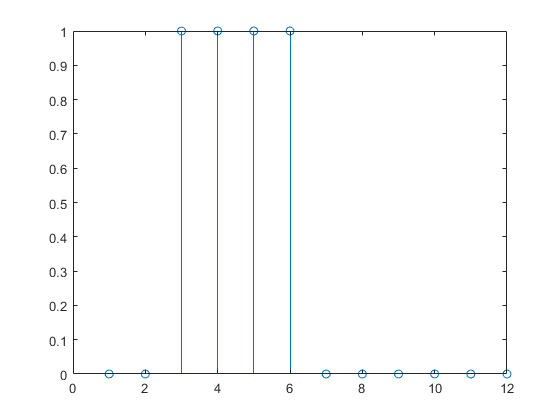
现在创建一个静态网络，并找到网络对脉冲序列的响应。使用以下命令创建一个简单的线性网络，该网络具有一个层、一个神经元、无偏置、权重为 2：

net = linearlayer;
net.inputs{1}.size = 1;
net.layers{1}.dimensions = 1;
net.biasConnect = 0;
net.IW{1,1} = 2;

view(net)

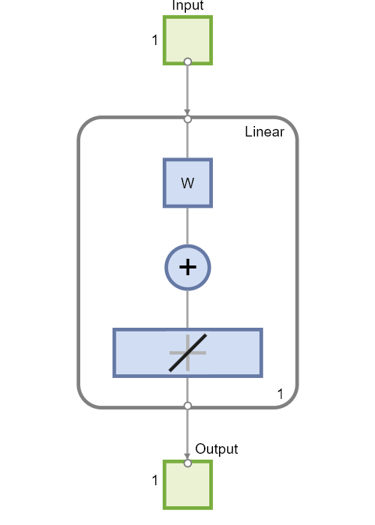
您现在可以仿真网络对脉冲输入的响应并进行绘图：

a = net(p);
stem(cell2mat(a))

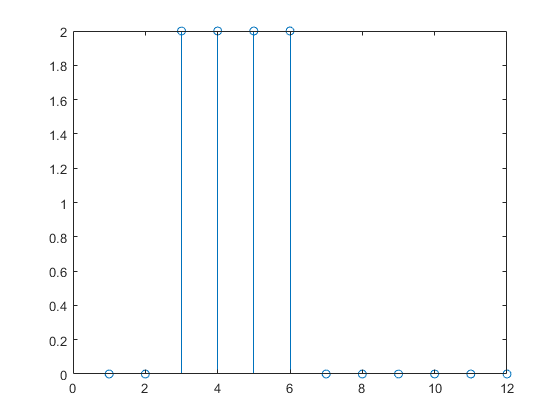
请注意，静态网络的响应持续时间与输入脉冲的持续时间一样长。静态网络在任何时间点的响应仅取决于该时间点时的输入序列的值。

现在创建一个动态网络，但该网络没有任何反馈连接（非循环网络）。您可以使用在动态网络中使用并发输入进行仿真中使用的相同网络，该网络是一个线性网络，输入端有一个抽头延迟线：

net = linearlayer([0 1]);
net.inputs{1}.size = 1;
net.layers{1}.dimensions = 1;
net.biasConnect = 0;
net.IW{1,1} = [1 1];

view(net)

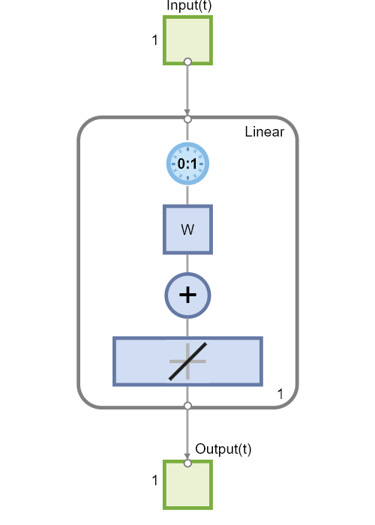
您可以再次仿真网络对脉冲输入的响应并进行绘图：

a = net(p);
stem(cell2mat(a))

动态网络的响应持续时间比输入脉冲的持续时间长。动态网络具有记忆能力。它在任何给定时间的响应不仅取决于当前输入，还取决于输入序列的历史记录。如果网络没有任何反馈连接，则只有有限的历史记录量会影响响应。在此图中，您可以看到对脉冲的响应在脉冲持续时间之后又持续了一个时间步。这是因为输入端抽头延迟线的最大延迟为 1。

现在假设有一个简单的循环动态网络，如下图所示。

您可以使用以下命令创建该网络、查看该网络以及对该网络进行仿真。设计时间序列 NARX 反馈神经网络中讨论了 narxnet 命令。

net = narxnet(0,1,[],'closed');
net.inputs{1}.size = 1;
net.layers{1}.dimensions = 1;
net.biasConnect = 0;
net.LW{1} = .5;
net.IW{1} = 1;
view(net)

使用以下命令绘制网络响应。

a = net(p);
stem(cell2mat(a))

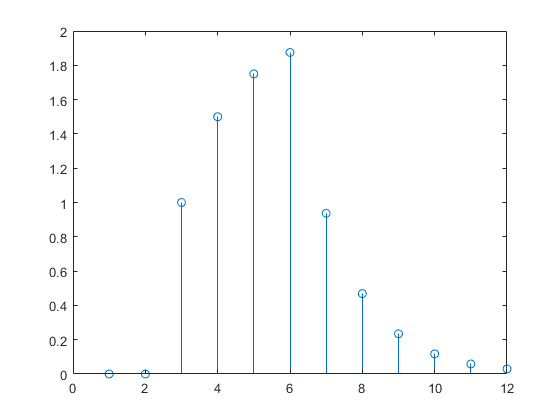
请注意，循环动态网络的响应时间通常比前馈动态网络的响应时间更长。对于线性网络，前馈动态网络称为有限冲激响应 (FIR)，因为对冲激输入的响应在有限时间后将变为零。线性循环动态网络被称为无限冲激响应 (IIR)，因为对冲激的响应可以向零方向衰减（对于稳定网络），但永远不会完全等于零。非线性网络的冲激响应无法定义，但有限响应和无限响应的概念确实延续了下来。

动态网络的应用

动态网络通常比静态网络更强大（但训练起来也更困难一些）。由于动态网络具有记忆能力，因此可以训练它们来学习顺序模式或时变模式。这在金融市场预测 [RoJa96]、通信系统中的通道均衡 [FeTs03]、电力系统中的相位检测 [KaGr96]、排序 [JaRa04]、故障检测 [ChDa99]、语音识别 [Robin94] 甚至遗传学中的蛋白质结构预测 [GiPr02] 等不同领域都有应用。您可以在 [MeJa00] 中找到关于更多动态网络应用的介绍。

动态神经网络的一个主要应用领域是控制系统。该应用在神经网络控制系统中有详细的介绍。动态网络也非常适合用于滤波。您将看到如何使用一些线性动态网络进行滤波，并且在本主题中，还使用非线性动态网络扩展了其中一些概念。

动态网络结构

Deep Learning Toolbox™ 软件旨在训练一类称为分层数字动态网络 (LDDN) 的网络。任何能以 LDDN 形式布局的网络都可以使用该工具箱进行训练。以下是 LDDN 的基本描述。

LDDN 中的每一层都由以下部分组成：

网络具有连接到特殊权重的输入，称为输入权重，用 IW^i,j 表示（代码中为 net.IW{i,j}），其中 j 表示传递到权重的输入向量数，i 表示权重所连接的层数。将一层与另一层相连接的权重称为层权重，用 LW^i,j 表示（代码中为 net.LW{i,j}），其中 j 表示传递到权重的层数，i 表示权重输出处的层数。

下图是一个三层 LDDN 示例。第一层有三个与之关联的权重：一个输入权重、一个第 1 层的层权重和一个第 3 层的层权重。两个层权重具有相关联的抽头延迟线。

Deep Learning Toolbox 软件可用于训练任何 LDDN，只要权重函数、净输入函数和传递函数具有导数即可。大多数常见的动态网络架构都可以用 LDDN 形式表示。在本主题的其余部分，您将了解如何使用一些简单的命令来创建和训练几个功能非常强大的动态网络。可以使用通用网络命令创建本主题未涉及的其他 LDDN 网络，具体说明请参阅定义浅层神经网络架构。

动态网络训练

在 Deep Learning Toolbox 软件中使用多层浅层神经网络与反向传播训练中所描述的基于梯度的算法训练动态网络。您可以从该主题中介绍的任何训练函数中进行选择。以下部分的内容提供了示例。

虽然可以使用与静态网络相同的基于梯度的算法训练动态网络，但动态网络上算法的性能可能会有很大不同，并且必须用更复杂的方式计算梯度。再次假设有下图所示的简单循环网络。

权重对网络输出有两种不同的影响。第一种是直接影响，因为权重的变化会导致当前时间步的输出立即发生变化。（这种影响可以使用标准反向传播来计算。）第二种是间接影响，因为层的一些输入（例如 a(t − 1)），也是权重的函数。为了考虑这种间接影响，您必须使用动态反向传播来计算梯度，而这会增加计算量。（请参阅 [DeHa01a]、[DeHa01b] 和 [DeHa07]。）预计动态反向传播需要更多的时间来训练，部分原因就在于此。此外，动态网络的误差曲面可能比静态网络的误差曲面更复杂。训练更有可能陷入局部最小值。这表明您可能需要多次训练网络才能获得最佳结果。有关动态网络训练的一些讨论，请参阅 [DHH01] 和 [HDH09]。

本主题的其余部分介绍如何创建、训练某些动态网络并将其应用于建模、检测和预测问题。有些网络需要使用动态反向传播来计算梯度，有些则不需要。作为用户，您无需决定是否需要使用动态反向传播。这是由软件自动确定的，软件还会决定要使用的最佳动态反向传播形式。您只需要创建网络，然后调用标准 train 命令即可。