本页面提供的是上一版软件的文档。当前版本中已删除对应的英文页面。

设计时间序列 NARX 反馈神经网络

要查看在开环形式、闭环形式和开环/闭环多步预测中应用 NARX 网络的示例，请参阅多步神经网络预测。

注意

要设计 NARX 模型，您还可以使用 System Identification Toolbox™。建议使用此工作流，因为它具有以下优势：

扩展线性 ARX 模型，并使用灵活的非线性函数（如小波网络、机器学习算法和神经网络）对复杂的非线性行为进行建模。
通过选择适当的回归量并从线性模型开始，将洞察和物理信息包含在系统中。

到目前为止讨论的所有特定动态网络或者是仅在输入层具有动态的专用网络，或者是前馈网络。外因输入非线性自回归网络 (NARX) 是循环动态网络，其反馈连接包含网络的几个层。NARX 模型基于线性 ARX 模型，该模型通常用于时间序列建模。

NARX 模型的定义方程是

$y (t) = f (y (t - 1), y (t - 2), \dots, y (t - n_{y}), u (t - 1), u (t - 2), \dots, u (t - n_{u}))$

其中从属输出信号 y(t) 的下一个值根据输出信号的先前值和独立（外因）输入信号的先前值进行回归。您可以通过使用前馈神经网络来逼近函数 f，从而实现 NARX 模型。生成的网络的图如下所示，其中两层前馈网络用于逼近。这种实现还支持向量 ARX 模型，其中输入和输出可以是多维的。

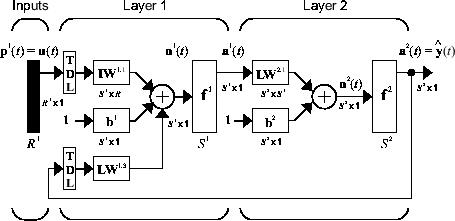
Diagram of a two-layer feedforward network

NARX 网络有许多应用。它可以用作预测器，预测输入信号的下一个值。它也可用于非线性滤波，其中目标输出是输入信号的无噪声版本。NARX 网络可用于另一个重要应用，即非线性动态系统的建模。

在说明 NARX 网络的训练之前，需要解释在训练中有用的一项重要配置。您可以将 NARX 网络的输出视为您尝试建模的某个非线性动态系统的输出估计值。输出会反馈到前馈神经网络的输入，这是标准 NARX 架构的一部分，如下方左图所示。由于在网络训练期间真实输出是可用的，因此您可以创建一个串并行架构（请参阅 [NaPa91]），其中使用真实输出而不是反馈估计的输出，如下方右图所示。这样有两个优点。第一，前馈网络的输入更准确。第二，生成的网络为纯前馈架构，可以使用静态反向传播进行训练。

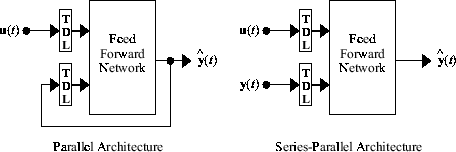
Comparison of a feedforward network with parallel architecture and a feedforward network with series-parallel architecture

下面显示如何使用串并行架构来训练 NARX 网络以进行动态系统建模。

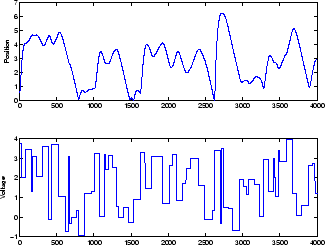
中开始描述的磁悬浮系统是一个 NARX 网络示例。下图中的底部图显示施加到电磁铁上的电压，顶部图显示永磁体的位置。以 0.01 秒的采样间隔采集数据，形成两个时间序列。

目标是为此磁悬浮系统开发一个 NARX 模型。

Plots of the position of the permanent magnet (top) and the voltage applied to the electromagnet (bottom)

首先，加载训练数据。使用将输入和输出都延迟两个数据点的抽头延迟线，因此训练从第三个数据点开始。串并行网络有两个输入，即 u(t) 序列和 y(t) 序列。

[u,y] = maglev_dataset;

使用函数 narxnet 创建串并行 NARX 网络。在隐藏层中使用 10 个神经元，并使用 trainlm 进行训练，然后使用 preparets 准备数据：

d1 = [1:2];
d2 = [1:2];
narx_net = narxnet(d1,d2,10);
narx_net.divideFcn = '';
narx_net.trainParam.min_grad = 1e-10;
[p,Pi,Ai,t] = preparets(narx_net,u,{},y);

（请注意，y 序列被视为反馈信号，它既是输入也是输出（目标）。稍后，当您实现闭环时，适当的输出将连接到适当的输入。）现在您已准备好训练网络。

narx_net = train(narx_net,p,t,Pi);

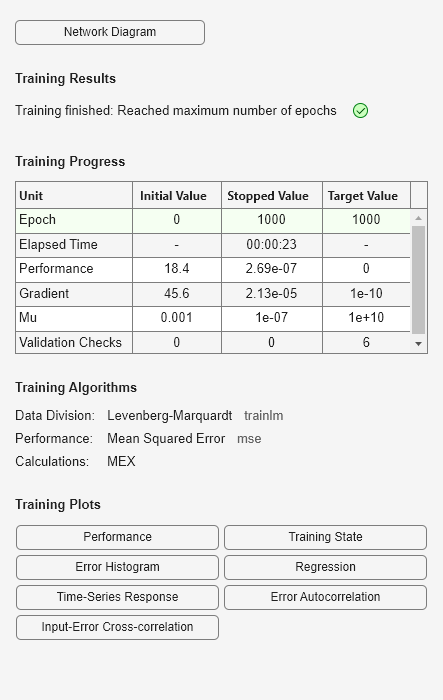
您现在可以仿真网络，并绘制这一串并行网络产生的误差。

yp = sim(narx_net,p,Pi);
e = cell2mat(yp)-cell2mat(t);
plot(e)

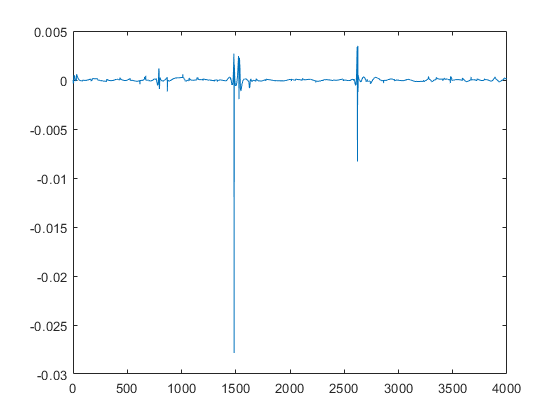
您可以看到误差非常小。然而，由于采用串并行配置，这些只是向前一步预测的误差。更严格的测试是将网络重新排列成原来的并行形式（闭环），然后执行多时间步的迭代预测。这就是出现了并行运算。

可使用工具箱函数 (closeloop) 将 NARX（及其他）网络从串并行配置（开环）转换为并行配置（闭环），前者适用于训练，后者适用于向前多步预测。以下命令演示如何将您刚刚训练的网络转换为并行形式：

narx_net_closed = closeloop(narx_net);

要查看两个网络之间的差异，可以使用查看命令：

view(narx_net)

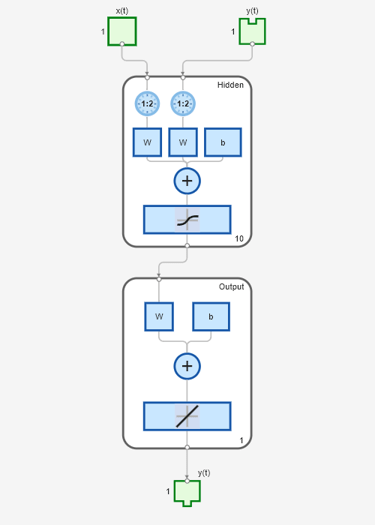
view(narx_net_closed)

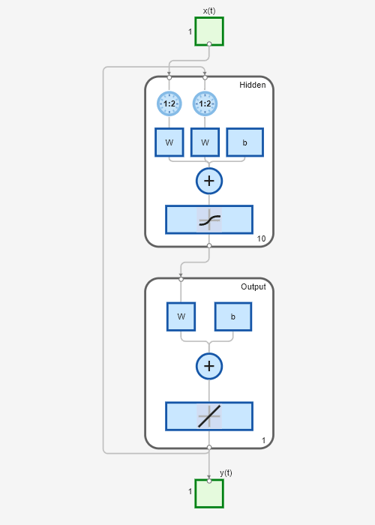
所有训练以开环（也称为串并行架构）形式完成，包括验证和测试步骤。典型的工作流是完全以开环方式创建网络，并且仅当网络经过训练（包括验证和测试步骤）后，它才会变换为闭环，以进行向前多步预测。同样，GUI 中的 R 值是基于开环训练结果进行计算的。

您现在可以使用闭环（并行）配置来执行 900 个时间步的迭代预测。在此网络中，您需要加载两个初始输入和两个初始输出作为初始条件。您可以使用 preparets 函数准备数据。它将使用网络结构来确定如何适当地划分和偏移数据。

y1 = y(1700:2600);
u1 = u(1700:2600);
[p1,Pi1,Ai1,t1] = preparets(narx_net_closed,u1,{},y1);
yp1 = narx_net_closed(p1,Pi1,Ai1);
TS = size(t1,2);
plot(1:TS,cell2mat(t1),'b',1:TS,cell2mat(yp1),'r')

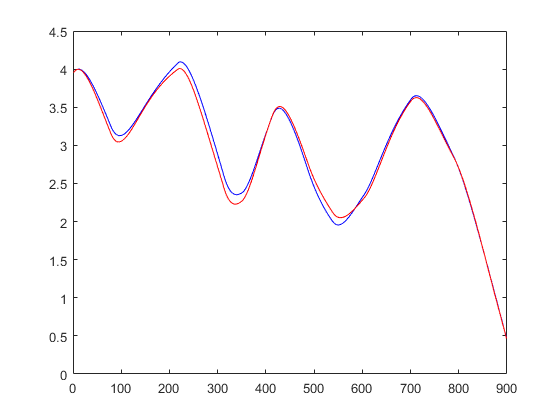
该图说明了迭代预测。蓝线表示磁体的实际位置，红线表示由 NARX 神经网络预测的位置。尽管网络向前预测了 900 个时间步，但预测非常准确。

为了使并行响应（迭代预测）准确，重要的是要对网络进行训练，使串并行配置（向前一步预测）中的误差非常小。

您还可以使用 narxnet 命令且将第四个输入参量设置为 'closed' 来创建并行（闭环）NARX 网络，并直接训练该网络。一般情况下，与串并行训练相比，此训练需要的时间更长，获得的实现性能也较差。

每次训练神经网络时，由于初始权重和偏置值不同，并且将数据划分为训练集、验证集和测试集的方式也不同，可能会产生不同的解。因此，针对同一问题训练的不同神经网络对同一输入可能给出不同输出。为确保找到准确度良好的神经网络，需要多次重新训练。

如果需要更高的准确度，可以采用几种其他方法来改进初始解。有关详细信息，请参阅提高浅层神经网络泛化能力，避免过拟合。

多个外部变量

磁悬浮示例说明如何用单一外部输入值对随时间变化的时间序列建模。但是，NARX 网络可以解决具有多个外部输入元素的问题，并预测具有多个元素的序列。在这些情况下，输入和目标由表示时间的行元胞数组组成，但每个元胞元素都是输入或目标信号的 N 个元素组成的 N×1 向量。

例如，此处有一个数据集，它由包含两个元素的外部变量组成，用于预测由单个元素组成的序列。

[X,T] = ph_dataset;

外部输入 X 格式化为由二元素向量组成的行元胞数组，每个向量表示酸和基底溶液流。目标表示溶液随时间变化而得到的 pH 值。

您可以使用函数 con2seq 将自己的多元素序列数据从矩阵形式重新格式化为神经网络时间序列形式。

训练网络的过程就像上面处理磁悬浮问题一样进行。

net = narxnet(10);
[x,xi,ai,t] = preparets(net,X,{},T);
net = train(net,x,t,xi,ai);
y = net(x,xi,ai);
e = gsubtract(t,y);

要查看在开环形式、闭环形式和开环/闭环多步预测中应用 NARX 网络的示例，请参阅多步神经网络预测。