了解浅层网络数据结构

本主题讨论输入数据结构的格式如何影响网络仿真。先讨论静态网络，然后继续讨论动态网络。下一节介绍数据结构的格式如何影响网络训练。

有两种基本类型的输入向量：并发（同时发生，或没有特定的时间顺序）的输入向量和按时间顺序发生的输入向量。对于并发向量，顺序并不重要，如果有多个网络并行运行，您可以为每个网络提供一个输入向量。对于顺序向量，向量出现的顺序很重要。

在静态网络中使用并发输入进行仿真

网络仿真的最简单情况是，要仿真的网络是静态的（没有反馈或延迟）。在这种情况下，您无需担心输入向量是否按特定时间顺序出现，因此您可以将输入视为并发的。此外，假设网络只有一个输入向量，问题会变得更加简单。以如下网络为例。

A neuron with vector input. The neuron receives input vector p, multiplies each element of p with an element of weight matrix w, sums the results and adds bias b, and then applies the purelin transfer function.

要设置此线性前馈网络，请使用以下命令：

net = linearlayer;
net.inputs{1}.size = 2;
net.layers{1}.dimensions = 1;

为简单起见，将权重矩阵和偏置分别赋值为 W = [1 2] 和 b = [0]。

用于进行这些赋值的命令为

net.IW{1,1} = [1 2];
net.b{1} = 0;

假设网络仿真数据集由 Q =4 个并发向量组成：

$p_{1} = [\begin{array}{l} 1 \\ 2 \end{array}], p_{2} = [\begin{array}{l} 2 \\ 1 \end{array}], p_{3} = [\begin{array}{l} 2 \\ 3 \end{array}], p_{4} = [\begin{array}{l} 3 \\ 1 \end{array}]$

并发向量以单个矩阵的形式提供给网络：

P = [1 2 2 3; 2 1 3 1];

您现在可以仿真网络：

A = net(P)
A =
     5     4     8     5

将由并发向量组成的单个矩阵提供给网络，网络生成并发向量的单个矩阵作为输出。如果有四个网络并行运行，并且每个网络接收其中一个输入向量并生成其中一个输出，则结果将是相同的。输入向量的顺序并不重要，因为它们不会互相交互。

在动态网络中使用顺序输入进行仿真

当网络包含延迟时，网络的输入通常是按特定时间顺序出现的一系列输入向量。为了说明这种情况，下图显示了一个包含单个延迟的简单网络。

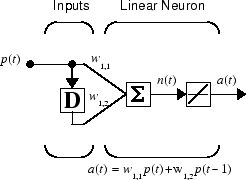
A neuron with two-element vector input. The neuron receives input vector p, applies a delay to only one element of p, multiplies each element of p with an element of weight matrix w, sums the results and adds bias b, and then applies the purelin transfer function.

使用以下命令创建该网络：

net = linearlayer([0 1]);
net.inputs{1}.size = 1;
net.layers{1}.dimensions = 1;
net.biasConnect = 0;

将权重矩阵赋值为 W = [1 2]。

对应命令为：

net.IW{1,1} = [1 2];

假设输入序列为：

$p_{1} = [1], p_{2} = [2], p_{3} = [3], p_{4} = [4]$

顺序输入作为元胞数组的元素提供给网络：

P = {1 2 3 4};

您现在可以仿真网络：

A = net(P)
A = 
    [1]    [4]    [7]    [10]

您输入一个包含一系列输入的元胞数组，然后网络生成一个包含一系列输出的元胞数组。当以序列形式提供输入时，输入的顺序很重要。在这种情况下，当前输出是通过将当前输入乘以 1，将前面的输入乘以 2，并将结果相加得到的。如果您要更改输入的顺序，则输出中得到的数字也会发生变化。

在动态网络中使用并发输入进行仿真

如果您要将相同的输入作为一组并发输入而不是序列输入来应用，则会获得完全不同的响应。（但是，目前尚不清楚为什么要使用动态网络执行此操作。）就好像每个输入都并发应用到一个单独的并行网络一样。对于前面的示例在动态网络中使用顺序输入进行仿真，如果您使用一组并发输入，则具有

$p_{1} = [1], p_{2} = [2], p_{3} = [3], p_{4} = [4]$

这可以使用以下代码来创建：

P = [1 2 3 4];

当您使用并发输入进行仿真时，您会获得

A = net(P)
A =
     1     2     3     4

结果与将每个输入并发应用到一个单独的网络并计算一个输出相同。请注意，由于您没有为网络延迟分配任何初始条件，因此假设它们为 0。对于这种情况，输出就是 1 乘以输入，因为乘以当前输入的权重是 1。

在某些特殊情况下，您可能希望同时仿真网络对多个不同序列的响应。在这种情况下，您可能希望为网络提供一组并发序列。例如，假设您想要为网络提供以下两个序列：

$\begin{matrix} p_{1} (1) = [1], p_{1} (2) = [2], p_{1} (3) = [3], p_{1} (4) = [4] \\ p_{2} (1) = [4], p_{2} (2) = [3], p_{2} (3) = [2], p_{2} (4) = [1] \end{matrix}$

输入 P 应该是一个元胞数组，其中数组的每个元素都包含同时发生的两个序列的两个元素：

P = {[1 4] [2 3] [3 2] [4 1]};

您现在可以仿真网络：

A = net(P);

生成的网络输出将为

A = {[1 4] [4 11] [7 8] [10 5]}

正如您所看到的，每个矩阵的第一列构成由第一个输入序列生成的输出序列，该输入序列是前面示例中使用的序列。每个矩阵的第二列构成由第二个输入序列生成的输出序列。两个并发序列之间没有交互。就好像它们每个都被应用到并行运行的单独网络一样。

下图显示了当 TS 时间步有 Q 个并发序列时网络输入 P 的一般格式。它涵盖了所有只有一个输入向量的情况。元胞数组的每个元素都是并发向量矩阵，这些向量对应于每个序列的同一时间点。如果有多个输入向量，则元胞数组中将有多行矩阵。

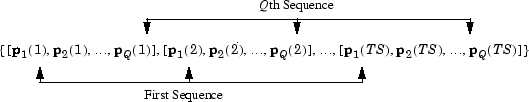
Format of the sequences

在本主题中，您将顺序输入和并发输入应用到动态网络。在在静态网络中使用并发输入进行仿真中，您将并发输入应用到了静态网络。也可以将顺序输入应用到静态网络。这不会改变网络的仿真响应，但会影响网络的训练方式。Neural Network Training Concepts中有清晰的解释。

另请参阅配置浅层神经网络输入和输出。