Solve PDE Using Fourier Neural Operator

Open Live Script

This example shows how to train a Fourier neural operator (FNO) neural network that outputs the solution of a partial differential equation (PDE).

A neural operator [1] is a type of neural network that maps between function spaces. For example, it can learn to output the solution to a PDE when given the initial conditions for the system. A Fourier neural operator (FNO) [2] is a neural operator that can learn these mappings more efficiently by leveraging Fourier transforms. In particular, for an input function $f$ in the spatial domain, the layers in the neural network learn the transformation $F$ such that $F (f) = f_{}^{ˆ}$ , where $f_{}^{ˆ}$ is the Fourier transform of $f$ . The FNO can then operate in the frequency domain. Using a neural network to predict the solutions of a PDE can be faster than computing the solutions numerically.

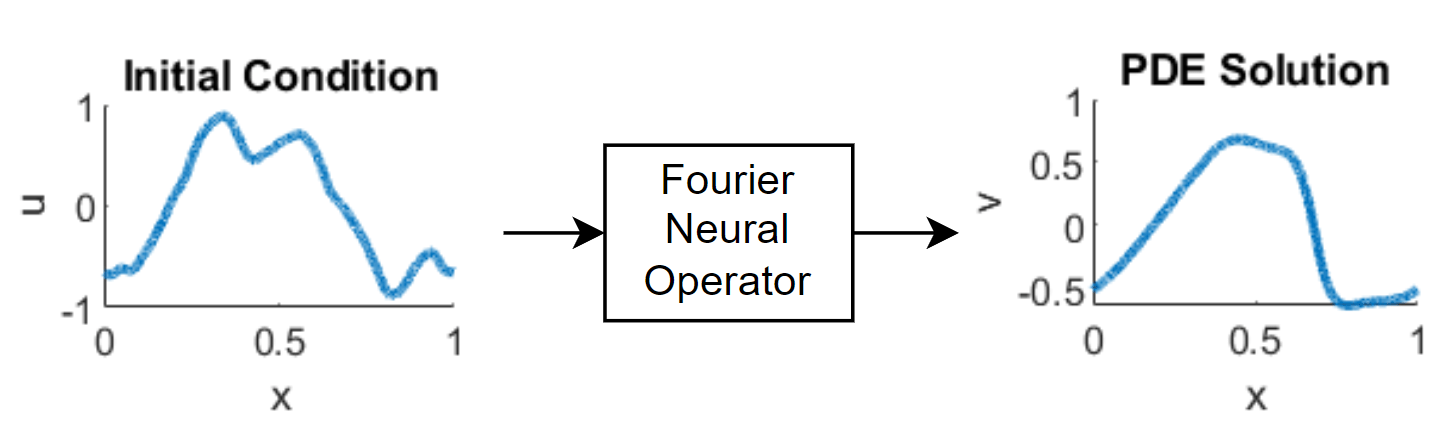
This diagram illustrates the flow of data through an FNO.

Diagram of data flowing through FNO. The input is a function labeled "Initial Condition". The output is a function labeled "PDE Solution".

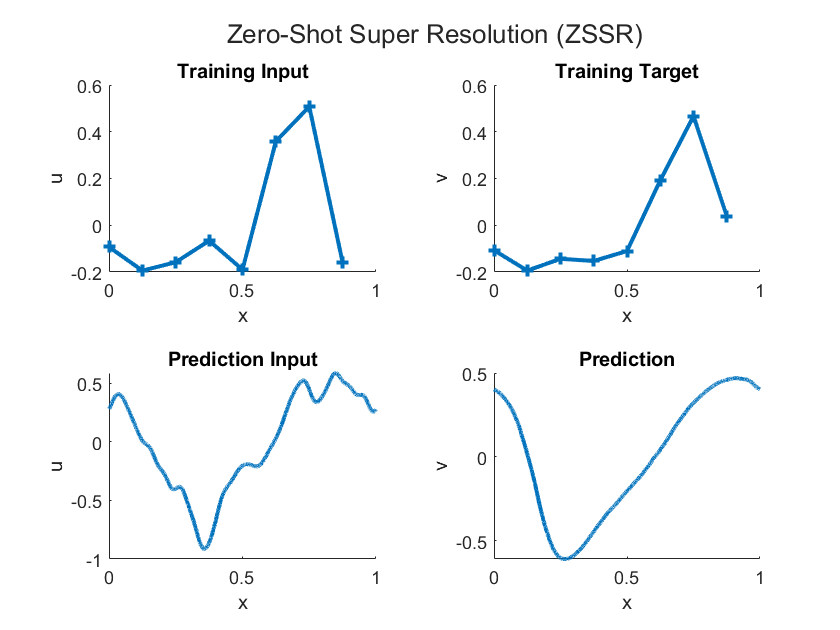
Because an FNO learns mappings between function spaces, you can evaluate the output function at a higher resolution than that of the training data. This functionality is known as zero-shot super-resolution (ZSSR). That is, ZSSR is the ability to enhance the resolution of the input and output data beyond the original training data, without the need for additional high-resolution examples. This diagram illustrates the differences between low-resolution training data and high-resolution inputs and outputs for prediction.

Plots showing low resolution and high resolution inputs and outputs. The low-resolution functions are composed of a small number of straight lines between points. The high-resolution functions are smooth curves.

This example trains an FNO to output the solutions to the 1-D Burgers' equation.

Load Training Data

Load the data for the 1-D Burgers' equation.

The Burgers' equation is a PDE that arises in different areas of applied mathematics, for example, in fluid mechanics, nonlinear acoustics, gas dynamics, and traffic flows. The PDE is:

$\frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} = \frac{1}{R e} \frac{\partial^{2} u}{\partial x^{2}}, x \in (0, 1), t \in (0, 1),$

where $R e$ is the Reynolds number. The initial conditions are:

$u (x, 0) = u_{0} (x), x \in (0, 1)$

The equation imposes periodic boundary conditions across the spatial domain with the initial condition $u_{0}$ to the solution at time $t = 1 : u_{0} ⟼ u (x, 1)$ .

Load the data for the 1-D Burgers' equation from burgers_data_R10.mat, which contains initial velocities $u_{0}$ and solutions $u (x, 1)$ of the Burgers' equation.

dataFile = "burgers_data_R10.mat";
if ~exist(dataFile,"file")
    location = "https://ssd.mathworks.com/supportfiles/nnet/data/burgers1d/burgers_data_R10.mat";
    websave(dataFile,location); 
end

data = load(dataFile,"a","u");
u0 = data.a;
u1 = data.u;

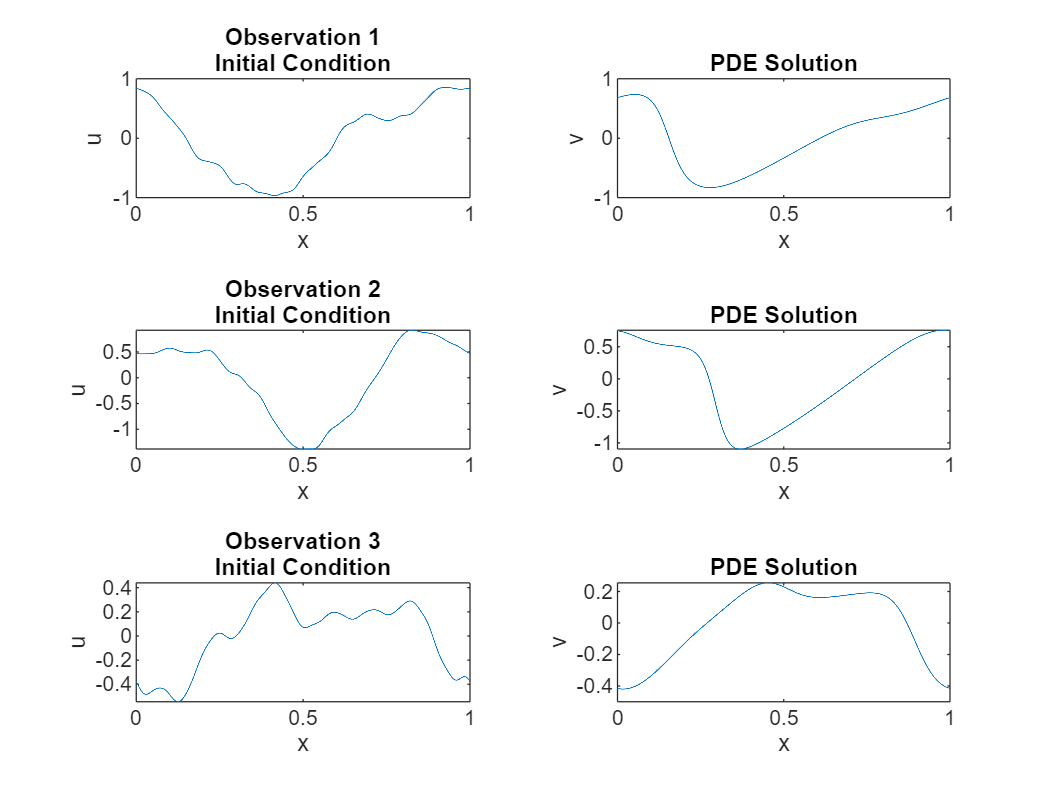
View some of the training data.

numPlots = 3;
gridSize = size(u0,2);
figure
tiledlayout(numPlots,2)
for i = 1:numPlots
    nexttile
    plot(linspace(0,1,gridSize),u0(i,:));
    title("Observation " + i + newline + "Initial Condition")
    xlabel("x")
    ylabel("u")

    nexttile
    plot(linspace(0,1,gridSize),u1(i,:));
    title("PDE Solution")
    xlabel("x")
    ylabel("v")
end

Prepare Training Data

Split the training and test data using the trainingPartitions function, attached to the example as a supporting file. To access this function, open the example as a live script. Use 80% of the data for training, 10% for validation, and the remaining 10% for testing.

numObservations = size(u0,1);
[idxTrain,idxValidation,idxTest] = trainingPartitions(numObservations,[0.8 0.1 0.1]);
U0Train = u0(idxTrain,:);
U1Train = u1(idxTrain,:);

U0Validation = u0(idxValidation,:);
U1Validation = u1(idxValidation,:);
U0Test = u0(idxTest,:);

To reduce the amount of processing in the FNO, downsample the training and validation data so that it has a grid size of 1024.

gridSizeDownsampled = 1024;
downsampleFactor = floor(gridSize./gridSizeDownsampled);

U0Train = U0Train(:,1:downsampleFactor:end);
U1Train = U1Train(:,1:downsampleFactor:end);
U0Validation = U0Validation(:,1:downsampleFactor:end);
U1Validation = U1Validation(:,1:downsampleFactor:end);

The FNO requires the input data to have a channel that corresponds to the spatial coordinates (the grid). Create the grid and concatenate it with the input data.

xMin = 0;
xMax = 1;
xGrid = linspace(xMin,xMax,gridSizeDownsampled);

xGridTrain = repmat(xGrid, [numel(idxTrain) 1]);
xGridValidation = repmat(xGrid, [numel(idxValidation) 1]);

U0Train = cat(3,U0Train,xGridTrain);
U0Validation = cat(3,U0Validation,xGridValidation);

View the sizes of the training and validation sets. The first, second, and third dimensions are the batch, spatial, and channel dimensions, respectively.

size(U0Train)

ans = 1×3

        1638        1024           2

size(U0Validation)

ans = 1×3

         204        1024           2

Define Neural Network Architecture

Define the neural network architecture. The network consists of multiple Fourier layers and convolution layers.

Define Fourier Layer

Define a function that creates a network layer that operates in the frequency domain.

The layer processes the input by applying convolutions and spectral convolutions and sums the outputs. This diagram illustrates the architecture of the layer.

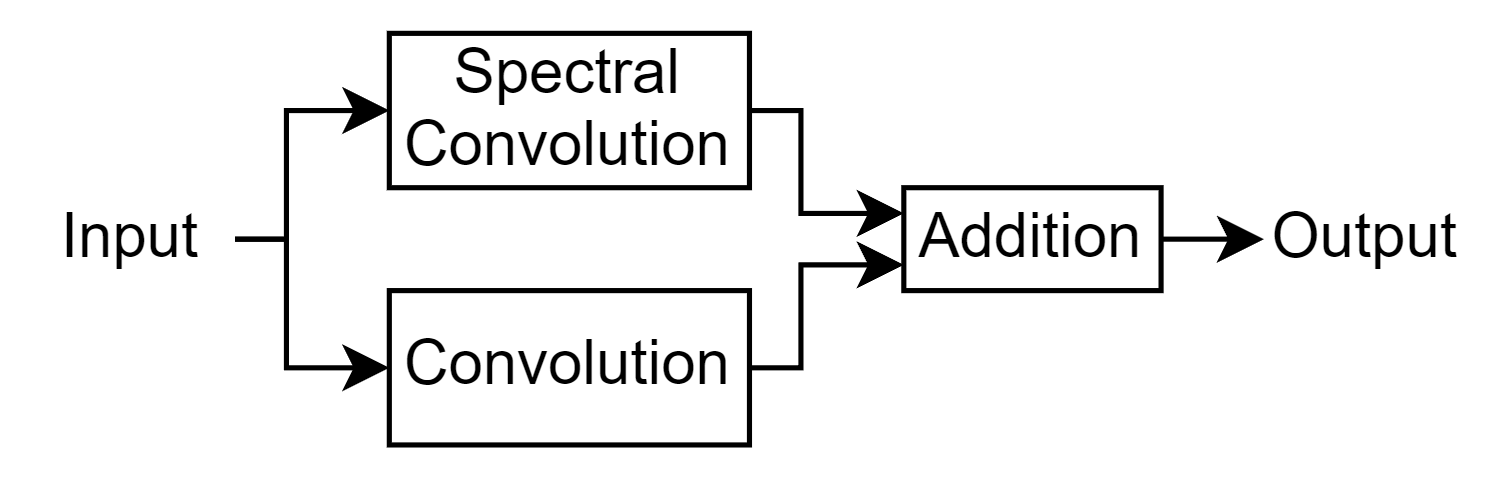
Diagram showing FNO layer architecture. The input is connected to both a spectral convolution layer and a convolution layer. The outputs of the two convolution layers are connected to an addition layer. The output of the FNO layer is the output of the addition layer.

A spectral convolutional layer applies convolutions in the frequency domain and is particularly useful for solving PDEs as it allows the network to learn complex spatial dependencies. To apply the spectral convolution operation, the Fourier layer uses the custom layer spectralConvolution1dLayer, attached to this example as a supporting file. To access this layer, open the example as a live script.

function layer = fourierLayer(spatialWidth,numModes,args)

arguments
    spatialWidth
    numModes
    args.Name = ""
end
name = args.Name;

net = dlnetwork;

layers = [
    identityLayer(Name="in")
    spectralConvolution1dLayer(spatialWidth,numModes,Name="specConv")
    additionLayer(2,Name="add")];

net = addLayers(net,layers);

layer = convolution1dLayer(1,spatialWidth,Name="fc");
net = addLayers(net,layer);

net = connectLayers(net,"in","fc");
net = connectLayers(net,"fc","add/in2");

layer = networkLayer(net,Name=name);

end

Create Neural Network

Define the neural network architecture. The network in this example consists of multiple Fourier-ReLU blocks connected in series.

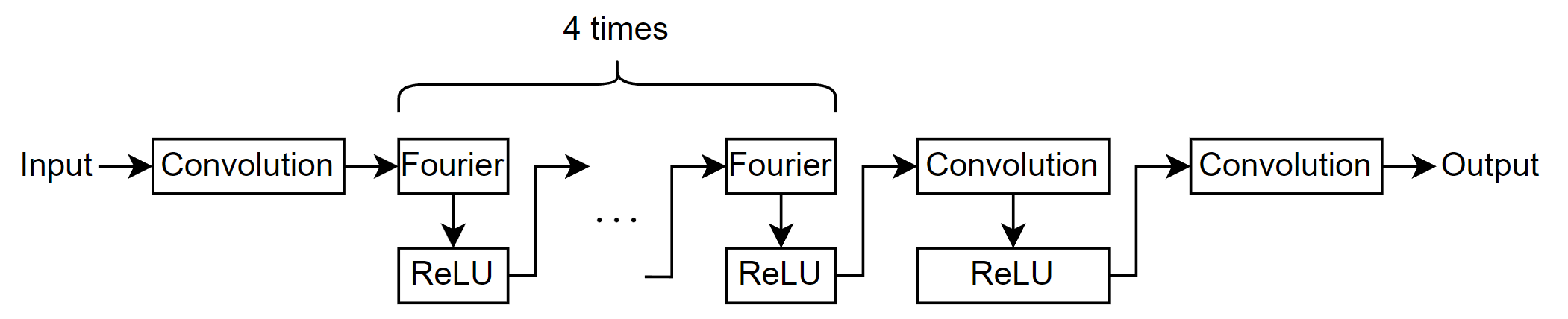
Diagram of the neural network of layers connected in series. From left to right, there is the input, convolution, four fourier-ReLU blocks, convolution, ReLU, convolution, and output.

Specify these options:

For the Fourier layers, specify 16 modes with a spatial width of 16.
Use an input layer of size [NaN spatialWidth 2], with format "BSC" (batch, spatial, channel), where spatialWidth is the spatial width of the Fourier layers.
Specify 128 1-by-1 filters for the convolution-ReLU block.
For the final convolutional layer, specify one 1-by-1 filter.

numModes = 16;
spatialWidth = 64; 

layers = [
    inputLayer([NaN spatialWidth 2],"BSC");
    convolution1dLayer(1,spatialWidth,Name="fc0")
    fourierLayer(spatialWidth,numModes,Name="fourier1");
    reluLayer
    fourierLayer(spatialWidth,numModes,Name="fourier2")
    reluLayer
    fourierLayer(spatialWidth,numModes,Name="fourier3")
    reluLayer
    fourierLayer(spatialWidth,numModes,Name="fourier4")
    reluLayer
    convolution1dLayer(1,128)
    reluLayer
    convolution1dLayer(1,1)];

Training Options

Specify the training options. Choosing among the options requires empirical analysis. To explore different training option configurations by running experiments, you can use the Experiment Manager app.

Train using the SGDM solver.
Train using a piecewise learning schedule, with an initial learning rate of 0.001 and a drop factor of 0.5.
Train for 30 epochs and with a mini-batch size of 20.
Shuffle the data every epoch.
Because the input data has dimensions that correspond to batch, spatial, and channel dimensions, specify the input data format as "BSC".
Monitor the training progress in a plot and specify the validation data.
Disable the verbose output.

schedule = piecewiseLearnRate(DropFactor=0.5);

options = trainingOptions("sgdm", ...
    InitialLearnRate=1e-3, ...
    LearnRateSchedule=schedule, ...
    MaxEpochs=30, ...
    MiniBatchSize=20, ...
    Shuffle="every-epoch", ...
    InputDataFormats="BSC", ...
    Plots="training-progress", ...
    ValidationData={U0Validation,U1Validation}, ...
    Verbose=false);

Define Relative $L_{2}$ Loss Function

Create the function relativeL2Loss, which takes the predictions and targets as input and returns the relative $L_{2}$ loss. The relative $L_{2}$ loss function is a variation of the $L_{2}$ loss function that accounts for scale by using the Euclidean norm of the difference between the predictions and targets and divides it by the Euclidean norm of the targets:

$R e l a t i v e L 2 (Y, T) = \sum_{n = 1}^{N} \frac{‖ T_{n} - Y_{n} ‖_{2}}{‖ T_{n} ‖_{2}}$

where:

$Y$ denotes the predictions.
$T$ denotes the targets.
$N$ denotes the number of observations.

function loss = relativeL2Loss(Y,T)

Y = stripdims(Y,"BSC");
T = stripdims(T,"BSC");

p = vecnorm(T-Y,2,2);
q = vecnorm(T,2,2);

loss = sum(p./q, 1);

end

Train Network

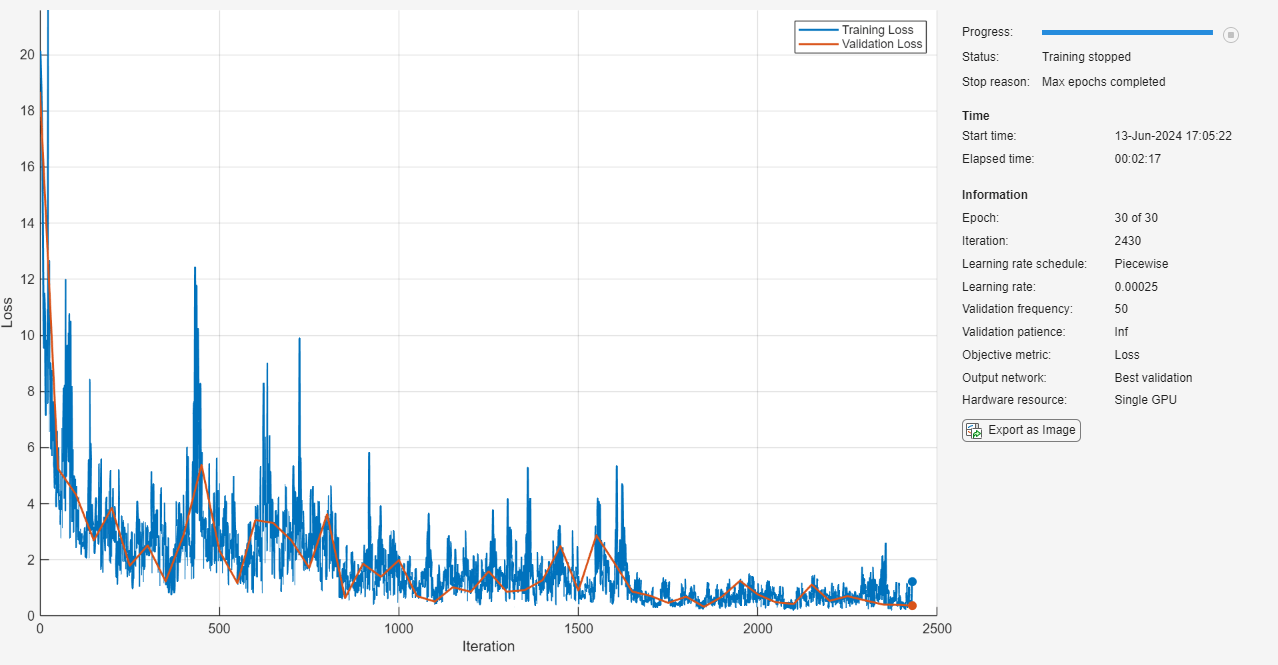
Train the neural network using the trainnet function. Use the custom loss function relativeL2Loss. By default, the trainnet function uses a GPU if one is available. Using a GPU requires a Parallel Computing Toolbox™ license and a supported GPU device. For information on supported devices, see GPU Computing Requirements (Parallel Computing Toolbox). Otherwise, the function uses the CPU. To select the execution environment manually, use the ExecutionEnvironment training option.

net = trainnet(U0Train,U1Train,layers,@relativeL2Loss,options);

Test Network

Test the prediction performance of the model by comparing the predictions on a held-out test set with the true labels and calculating the root mean squared error (RMSE).

Downsample the test data and concatenate the grid using the same steps as used for the training data.

xGridTest = repmat(xGrid, [numel(idxTest) 1]);

U0Test = U0Test(:,1:downsampleFactor:end);
U0Test = cat(3,U0Test,xGridTest);

U1Test = u1(idxTest,:);
U1Test = U1Test(:,1:downsampleFactor:end);

Test the neural network using the testnet function. By default, the testnet function uses a GPU if one is available. Otherwise, the function uses the CPU. To select the execution environment manually, use the ExecutionEnvironment argument of the testnet function.

rmseTest = testnet(net,U0Test,U1Test,"rmse")

rmseTest = 
0.0112

To evaluate the accuracy of the ZSSR, test the network using the test data without downsampling it.

xGridZSSR = linspace(xMin,xMax,gridSize);
xGridTestZSSR = repmat(xGridZSSR, [numel(idxTest) 1]);

U0TestZSSR = u0(idxTest,:);
U0TestZSSR = cat(3,U0TestZSSR,xGridTestZSSR);
U1TestZSSR = u1(idxTest,:);

rmseTestZSSR = testnet(net,U0TestZSSR,U1TestZSSR,"rmse")

rmseTestZSSR = 
0.0113

Make Predictions with New Data

Use the neural network to make a prediction.

Load the new data. For example purposes, use the first three test observations.

dataNew = u0(idxTest(1:3),:);
numObservationsNew = size(dataNew,1);

Calculate the grid size and concatenate it with the data.

gridSizeNew = size(dataNew,2);
xGridNew = linspace(xMin,xMax,gridSizeNew);
xGridNew = repmat(xGridNew, [size(dataNew,1) 1]);
U0New = cat(3,dataNew,xGridNew);

Make predictions using the minibatchpredict function. By default, the minibatchpredict function uses a GPU if one is available. Otherwise, the function uses the CPU. To select the execution environment manually, use the ExecutionEnvironment option.

Y = minibatchpredict(net,U0New);

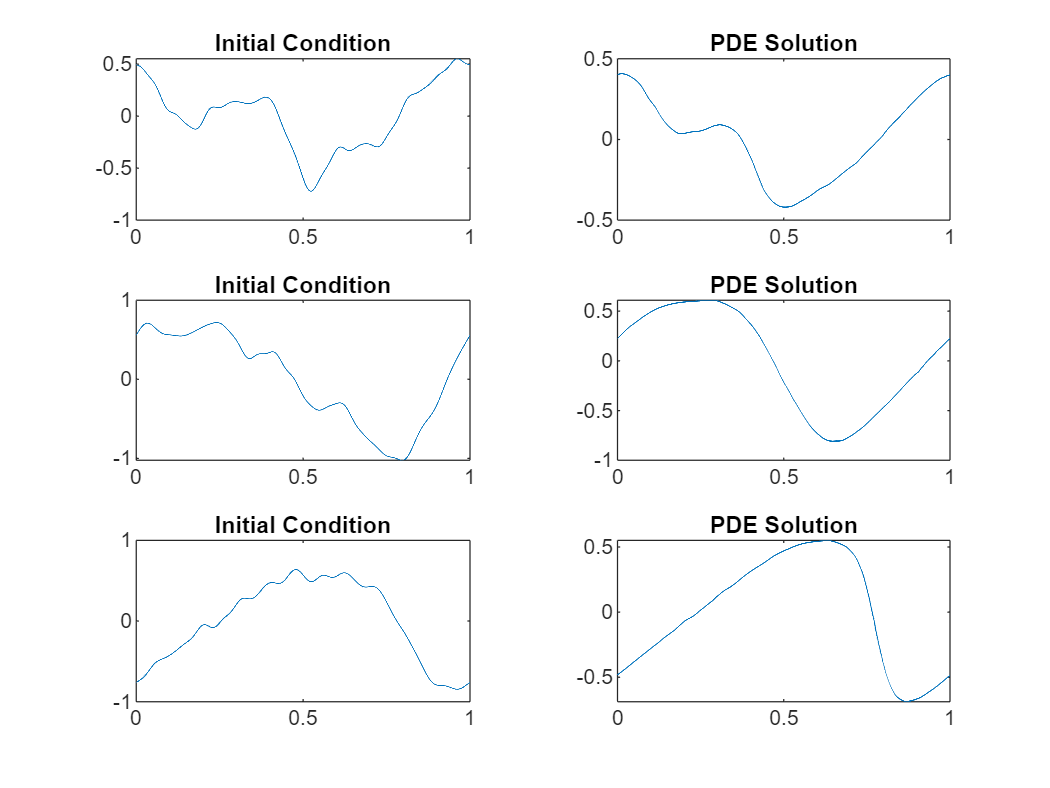
Visualize the predictions in a plot.

figure
tiledlayout("flow")
for i = 1:numObservationsNew
    nexttile
    plot(xGridNew(i,:),dataNew(i,:))
    title("Initial Condition")

    nexttile
    plot(xGridNew(i,:),Y(i,:))
    title("PDE Solution")
end

References

Li, Zongyi, Nikola Kovachki, Kamyar Azizzadenesheli, Burigede Liu, Kaushik Bhattacharya, Andrew Stuart, and Anima Anandkumar. “Neural Operator: Graph Kernel Network for Partial Differential Equations.” arXiv, March 6, 2020. http://arxiv.org/abs/2003.03485.
Li, Zongyi, Nikola Kovachki, Kamyar Azizzadenesheli, Burigede Liu, Kaushik Bhattacharya, Andrew Stuart, and Anima Anandkumar. “Fourier Neural Operator for Parametric Partial Differential Equations,” 2020. https://openreview.net/forum?id=c8P9NQVtmnO.

Solve PDE Using Fourier Neural Operator

Load Training Data

Prepare Training Data

Define Neural Network Architecture

Define Fourier Layer

Create Neural Network

Training Options

Define Relative $L_{2}$ Loss Function

Train Network

Test Network

Make Predictions with New Data

References

See Also

Related Topics

Solve PDE Using Fourier Neural Operator

Load Training Data

Prepare Training Data

Define Neural Network Architecture

Define Fourier Layer

Create Neural Network

Training Options

Define Relative L2 Loss Function

Train Network

Test Network

Make Predictions with New Data

References

See Also

Related Topics

Define Relative $L_{2}$ Loss Function