训练与应用多层浅层神经网络
提示
要训练深度学习网络,请使用 trainnet。
本主题介绍典型多层浅层网络工作流的一部分。有关详细信息和其他步骤,请参阅多层浅层神经网络与反向传播训练。
当初始化网络权重和偏置后,网络已准备好进行训练。多层前馈网络可以训练用于函数逼近(非线性回归)或模式识别。训练过程需要一组适当的网络行为示例 - 网络输入 p 和目标输出 t。
根据网络性能函数 net.performFcn 的定义,训练神经网络的过程包括调整网络的权重和偏置值以优化网络性能。前馈网络的默认性能函数是均方误差 mse - 网络输出 a 和目标输出 t 之间的平均平方误差。其定义如下:
(单个平方误差也可以加权。请参阅Train Neural Networks with Error Weights。实现训练有两种不同方式:增量模式和批量模式。在增量模式下,在将每个输入应用于网络后计算梯度并更新权重。在批量模式下,在训练集中的所有输入都应用于网络后再更新权重。本主题介绍使用 train 命令的批量模式训练。Incremental Training with adapt中讨论使用 adapt 命令的增量训练。对于大多数问题,当使用 Deep Learning Toolbox™ 软件时,批量训练比增量训练快得多,产生的误差也更小。
对于训练多层前馈网络,任何标准数值优化算法都可用于优化性能函数,但有几个关键算法已显示出对神经网络训练有优异性能。这些优化方法或者使用网络性能关于网络权重的梯度,或者使用网络误差关于权重的雅可比矩阵。
梯度和雅可比矩阵使用的计算方法称为反向传播算法,该算法涉及在网络中反向执行计算。反向传播计算是使用微积分的链式法则求导的,在 [HDB96] 的第 11 章(针对梯度)和第 12 章(针对雅可比矩阵)中讲述。
训练算法
为了说明训练的工作原理,以最简单的优化算法 - 梯度下降为例。它会沿着性能函数下降最快的方向(梯度的负方向)上更新网络权重和偏置。该算法的一次迭代可以写为如下形式
其中,xk 是当前权重和偏置的向量,gk 是当前梯度,αk 是学习率。此方程会一直迭代,直到网络收敛。
下表列出了 Deep Learning Toolbox 软件中可用的使用基于梯度或雅可比矩阵方法的训练算法。
有关这些方法的详细说明,另请参阅以下著作:Hagan, M.T., H.B. Demuth, and M.H. Beale, Neural Network Design, Boston, MA:PWS Publishing, 1996,第 11 和 12 章。
函数 | 算法 |
|---|---|
莱文贝格-马夸特 | |
贝叶斯正则化 | |
BFGS 拟牛顿 | |
弹性反向传播 | |
量化共轭梯度 | |
带鲍威尔/比尔重启的共轭梯度 | |
弗莱彻-鲍威尔共轭梯度 | |
波拉克-里比埃尔共轭梯度 | |
单步正割 | |
可变学习率梯度下降 | |
带动量的梯度下降 | |
梯度下降 |
最快的训练函数通常是 trainlm,它是 feedforwardnet 的默认训练函数。拟牛顿法 trainbfg 也相当快。这两种方法对于大型网络(具有数千个权重)往往效率较低,因为它们需要更多内存和更多计算时间。此外,trainlm 在函数拟合(非线性回归)问题上的性能优于模式识别问题。
在训练大型网络和模式识别网络时,trainscg 和 trainrp 是不错的选择。其内存要求相对较小,但比标准梯度下降算法要快得多。
请参阅选择多层神经网络训练函数,了解上表所示的训练算法性能的全面比较。
注意,术语“反向传播”在应用于神经网络训练时,有时特指梯度下降算法。此处不使用该术语,因为上述所有训练函数都涉及在网络中反向执行计算来求出梯度和雅可比矩阵的过程。所以,相较于反向传播,使用具体优化算法的名称会更清楚。
此外,多层网络有时也称为反向传播网络。不过,用于计算多层网络中的梯度和雅可比矩阵的反向传播方法也可应用于许多不同网络架构。事实上,任何具有可微分传递函数、权重函数和净输入函数的网络的梯度和雅可比矩阵都可以通过反向传播过程使用 Deep Learning Toolbox 软件来计算。您甚至可以创建自己的自定义网络,然后使用上表中的任何训练函数对它们进行训练。梯度和雅可比矩阵将自动为您计算。
训练示例
要演示训练过程,请执行以下命令:
load bodyfat_dataset
net = feedforwardnet(20);
[net,tr] = train(net,bodyfatInputs,bodyfatTargets);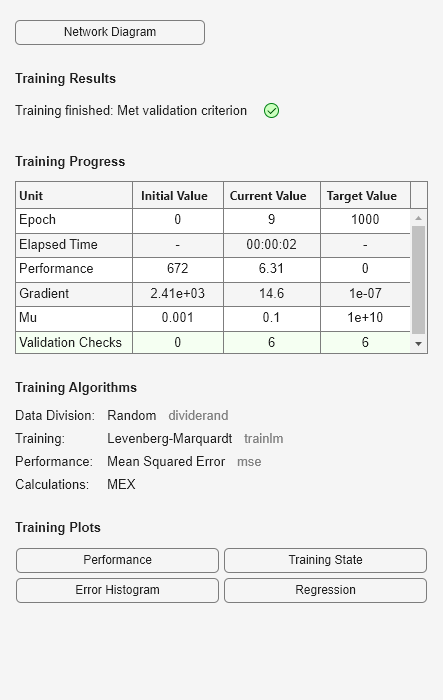
请注意,您不需要发出 configure 命令,因为配置是由 train 函数自动完成的。训练期间将出现训练窗口,如下图所示。(如果您不想在训练期间显示此窗口,可以将参数 net.trainParam.showWindow 设置为 false。如果您要在命令行中显示训练信息,可以将参数 net.trainParam.showCommandLine 设置为 true。)
此窗口显示数据已使用 dividerand 函数进行划分,并且使用了莱文贝格-马夸特 (trainlm) 训练方法和均方误差性能函数。上面提到过,这些是 feedforwardnet 的默认设置。
在训练期间,进度会在训练窗口中不断更新。最感兴趣的是性能、性能梯度的幅值和验证检查的数量。梯度的幅值和验证检查的数量用于终止训练。当训练达到性能的最小值时,梯度将变得非常小。如果梯度的幅值小于 1e-5,训练将停止。该限制可通过设置参数 net.trainParam.min_grad 进行调整。验证检查的数量表示验证性能无法降低的连续迭代次数。如果该数字达到 6(默认值),训练将停止。在本次运行中,您可以看到鉴于验证检查的数量,训练确实停止了。您可以通过设置参数 net.trainParam.max_fail 来更改此条件。(请注意,因为初始权重和偏置的随机设置,您的结果可能不同于训练图所示的结果。)
还有其他条件可用于停止网络训练。下表列出了这些条件。
参数 | 停止条件 |
|---|---|
min_grad | 最小梯度幅值 |
max_fail | 验证增加的最大数量 |
time | 最大训练时间 |
goal | 最低性能值 |
epochs | 最大训练轮数(迭代数) |
如果您点击训练窗口中的停止按钮,训练也将停止。如果性能函数在多次迭代中未显著降低,您可能需要这样做。通过重新发出上面所示的 train 命令,始终可以继续训练。它将从上一次运行完成的状态继续训练网络。
在训练窗口中,您可以访问四个图:性能、训练状态、误差直方图和回归。性能图显示性能函数值对迭代序号的图。它对训练、验证和测试性能绘图。训练状态图显示其他训练变量的进度,例如梯度幅值、验证检查的数量等。误差直方图显示网络误差的分布。回归图显示网络输出和网络目标之间的回归。您可以使用直方图和回归图来验证网络性能,如分析训练后的浅层神经网络性能中所述。
使用网络
在网络经过训练和验证后,网络对象可用于计算网络对任何输入的响应。例如,如果您要在构造数据集中找到对第五个输入向量的网络响应,可以使用以下命令
a = net(bodyfatInputs(:,5))
a = 27.3740
如果尝试此命令,输出可能会有所不同,具体取决于网络初始化时随机数生成器的状态。下面,调用网络对象来计算体脂数据集中所有输入向量的并发集合的输出。这是批量模式的仿真,其中所有输入向量都放在一个矩阵中。这比一次提交一个向量要高效得多。
a = net(bodyfatInputs);
每次训练神经网络时,由于初始权重和偏置值不同,并且将数据划分为训练集、验证集和测试集的方式也不同,可能会产生不同的解。因此,针对同一问题训练的不同神经网络对同一输入可能给出不同输出。为确保找到准确度良好的神经网络,需要多次重新训练。
如果需要更高的准确度,可以采用几种其他方法来改进初始解。有关详细信息,请参阅提高浅层神经网络泛化能力,避免过拟合。