Lowpass IIR Filter Design

Design lowpass IIR filter with tunable filter specifications

Since R2023b

Libraries:
DSP System Toolbox / Filtering / Filter Sources

Description

Use the Lowpass IIR Filter Design block to design a lowpass IIR filter using the Butterworth, Chebyshev Type I and the Chebyshev Type II design methods. You can tune the filter design specifications such as the filter order, 3-dB cutoff frequency, passband ripple, and the stopband attenuation during simulation. When the values of these parameters change, the block redesigns the filter and outputs the numerator and denominator coefficients in the second-order section (SOS) form.

Examples

expand all

Filter Noisy Signal Using Second-Order Section (SOS) Lowpass Filter in Simulink

This example uses:

Open Model

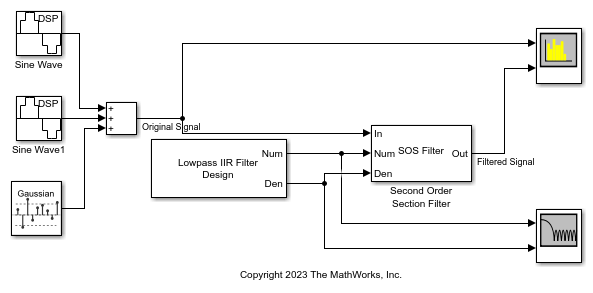
Filter a noisy sinusoidal signal using the Second-Order Section Filter block. Obtain the numerator and denominator coefficients of the SOS filter using the Lowpass IIR Filter Design block.

Tune the frequency specifications of the SOS filter during simulation.

Open and Run Model

Open the secondordersectionfilter_lowpass model by clicking the Open Model button.

The input signal in the model is a sum of two sine waves with the frequencies of 100 Hz and 350 Hz. The sample rate is 1000 Hz and the number of samples in each frame is 1024. The Random Source block adds zero-mean white Gaussian noise with a variance of 1e-4 to the sum of the sine waves.

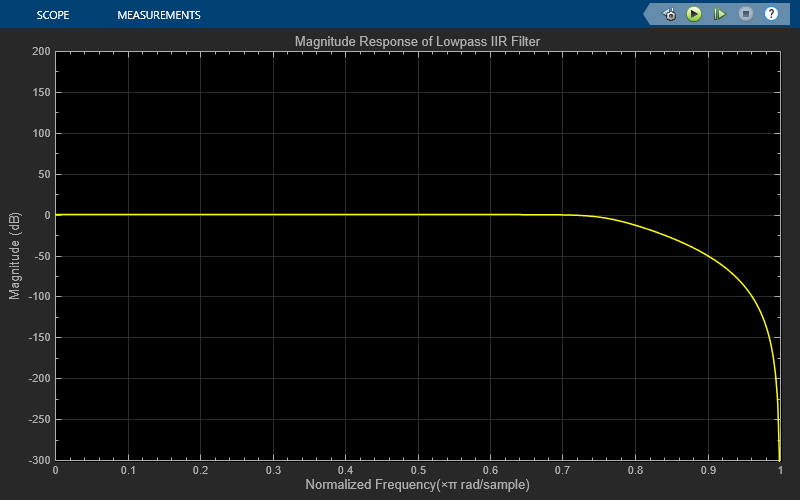
The Lowpass IIR Filter Design block designs a sixth-order lowpass IIR filter with the 3-dB cutoff frequency of 0.25 ${\pi}$ rad/sample. The block generates coefficients as a cascade of second-order sections. Visualize the frequency response of the filter using the Filter Visualizer.

Run the model.

The Second-Order Section Filter block filters the noisy sinusoidal signal and attenuates the second tone at 350 Hz. Visualize the original sinusoidal signal and the filtered signal using the Spectrum Analyzer.

Tune Frequency Specifications of SOS Filter

During simulation, you can tune the frequency specifications of the SOS filter by tuning the frequency parameters in the Lowpass IIR Filter Design block. The frequency response of the SOS filter updates accordingly.

Change the 3-dB cutoff frequency to 0.75 ${\pi}$ rad/sample in the Lowpass IIR Filter Design block. To change the parameter values more gradually during simulation, select the Smooth tuned filter parameters check box and specify a smoothing factor in the Lowpass IIR Filter Design block dialog box. The smoothing factor determines the speed at which the parameter values change until they match the desired new value. If you specify a smoothing factor of 0, the block does not smooth the parameter and immediately sets the parameter to the new value. As the smoothing factor approaches 1, the number of smoothing operations, and consequently, the number of filter redesigns increase. This example uses a smoothing factor of 0.6.

When you change the 3-dB cutoff frequency to 0.75 ${\pi}$ rad/sample, the second tone of the sinusoidal signal is now unaffected as it falls in the passband region of the filter.

Ports

Input

expand all

N — Filter order
positive integer

Specify the filter order as a positive integer. You can change the filter order you input through this port during simulation.

Dependencies

To enable this port, select the Specify filter order from input port parameter.

Fc — 3-dB cutoff frequency
positive scalar ≤ 1

Specify the 3-dB cutoff frequency of the filter in the normalized frequency units as a positive scalar less than or equal to 1. You can change the 3-dB cutoff frequency you input through this port during simulation.

Dependencies

To enable this port, select the Specify 3-dB cutoff frequency from input port parameter.

Data Types: single | double

Ap — Passband ripple in dB
positive scalar

Specify the passband ripple of the Chebyshev Type I filter as a positive scalar in dB. You can change the passband ripple you input through this port during simulation.

Dependencies

To enable this port:

Set the Design method parameter to Chebyshev Type I.
Select the Specify the passband ripple from input port parameter.

Data Types: single | double

Ast — Stopband attenuation in dB
positive scalar

Specify the stopband attenuation of the Chebyshev Type II filter as a positive scalar in dB. You can change the stopband attenuation you input through this port during simulation.

Dependencies

To enable this port:

Set the Design method parameter to Chebyshev Type II.
Select the Specify the stopband attenuation from input port parameter.

Data Types: single | double

Output

expand all

Num — Numerator coefficients
P-by-3 matrix

Numerator coefficients, returned as a P-by-3 matrix (SOS form), where P is the maximum number of filter sections.

$b = [\begin{matrix} b_{01} & b_{11} & b_{21} \\ b_{02} & b_{12} & b_{22} \\ ⋮ & ⋮ & ⋮ \\ b_{0 P} & b_{1 P} & b_{2 P} \end{matrix}]$

This equation represents the SOS filter in the transfer function form.

$H (z) = \prod_{k = 1}^{P} H_{k} (z) = \prod_{k = 1}^{P} \frac{b_{0 k} + b_{1 k} z^{- 1} + b_{2 k} z^{- 2}}{a_{0 k} + a_{1 k} z^{- 1} + a_{2 k} z^{- 2}},$

where

b is a matrix of numerator coefficients.
a is a matrix of denominator coefficients that the block outputs at the Den output port.
k is the row index.

P equals ceil(N_max/2), where N_max is the value of the Filter maximum order parameter.

When the actual filter order N is less than the maximum filter order N_max, the last ceil(N_max/2) − ceil(N/2) sections are trivial with coefficients [b₀, b₁, b₂] = [1, 0, 0].

When the actual filter order N is odd, the last nontrivial filter section has the coefficients [b₀, b₁, 0] = [1, 1, 0].

The data type of this port depends on the value of the Output data type parameter.

Data Types: single | double

Den — Denominator coefficients
P-by-3 matrix

Denominator coefficients, returned as a P-by-3 matrix (SOS form), where P is the maximum number of filter sections.

$a = [\begin{matrix} a_{01} & a_{11} & a_{21} \\ a_{02} & a_{12} & a_{22} \\ ⋮ & ⋮ & ⋮ \\ a_{0 P} & a_{1 P} & a_{2 P} \end{matrix}]$

This equation represents the SOS filter in the transfer function form.

$H (z) = \prod_{k = 1}^{P} H_{k} (z) = \prod_{k = 1}^{P} \frac{b_{0 k} + b_{1 k} z^{- 1} + b_{2 k} z^{- 2}}{a_{0 k} + a_{1 k} z^{- 1} + a_{2 k} z^{- 2}},$

where

a is a matrix of denominator coefficients and the leading denominator coefficient a₀ is always 1.
b is a matrix of numerator coefficients that the block outputs at the Num port.
k is the row index.

P equals ceil(N_max/2), where N_max is the value of the Filter maximum order parameter.

When the actual filter order N is less than the maximum filter order N_max, the last ceil(N_max/2) − ceil(N/2) sections are trivial with coefficients [a₀, a₁, a₂] = [1, 0, 0].

When the actual filter order N is odd, the last nontrivial filter section has the coefficients [1, a₁, 0] = [1, 1, 0].

The data type of this port depends on the value of the Output data type parameter.

Data Types: single | double

g — Scale values for each second-order section
vector

Scale values for each second-order section, returned as a vector with P + 1 elements, where P is the maximum number of filter sections and equals ceil(N_max/2), where N_max is the value of the Filter maximum order parameter.

Tunable: Yes

Dependencies

To enable this port, select the Design has scale values parameter.

Data Types: single | double

Parameters

expand all

Smooth tuned filter parameters — Smooth tuned filter parameters
`off` (default) | `on`

Since R2024a

When you select this check box, the block updates the tunable filter parameters such as the filter order, cutoff frequency, passband ripple, and stopband attenuation gradually by repeatedly designing the filter with intermediate values of the parameter until the parameter reaches the desired value. This process is called parameter smoothing. For more information, see Parameter Smoothing.

When you clear this check box, the block redesigns the filter with the new parameter value immediately.

Smoothing factor — Smoothing factor
0.6 (default) | nonnegative scalar less than 1

Since R2024a

Specify the smoothing factor α as a nonnegative scalar less than 1. When α = 0, no smoothing occurs. As α approaches 1, the number of smoothing operations, and consequently, the number of filter redesigns increase.

Tunable: Yes

Dependencies

To enable this parameter, select the Smooth tuned filter parameters parameter.

Design method — Filter design method
`Butterworth` (default) | `Chebyshev Type I` | `Chebyshev Type II`

Specify the filter design method as one of these:

Butterworth
Chebyshev Type I
Chebyshev Type II

Specify filter order from input port — Flag to specify filter order from input port
`off` (default) | `on`

Select this parameter to specify the filter order from the input port N. When you clear this parameter, you can specify the filter order in the block dialog box using the Filter order parameter.

Filter order — Filter order
`6` (default) | positive integer

Specify the filter order as a positive integer less than or equal to the value of the Filter maximum order parameter.

Tunable: Yes

Dependencies

To enable this parameter, clear the Specify filter order from input port parameter.

Filter maximum order — Maximum order of filter
`10` (default) | positive integer

Specify the maximum order of the filter as a positive integer. The value you specify in the Filter order parameter must be less than or equal to the value you specify in the Filter maximum order parameter.

Design has scale values — Specify if filter has scale values for each section
`off` (default) | `on`

Specify if the filter has scale values for each section. When you select this parameter, the block outputs the scale values through the g output port.

Specify 3-dB cutoff frequency from input port — Flag to specify 3-dB cutoff frequency from input port
`off` (default) | `on`

Select this parameter to specify the 3-dB filter cutoff frequency from the input port Fc. When you clear this parameter, you can specify the cutoff frequency in the block dialog box using the 3-dB cutoff frequency parameter.

3-dB cutoff frequency — 3-dB cutoff frequency
`0.25` (default) | positive scalar ≤ 1

Specify the 3-dB cutoff frequency of the filter in the normalized frequency units as a positive scalar less than or equal to 1.

Tunable: Yes

Dependencies

To enable this parameter, clear the Specify 3-dB cutoff frequency from input port parameter.

Data Types: single | double

Specify the passband ripple from input port — Flag to specify passband ripple from input port
`off` (default) | `on`

Select this parameter to specify the passband ripple from the input port Ap. When you clear this parameter, you can specify the passband ripple in the block dialog box using the Passband ripple (dB) parameter.

Dependencies

To enable this parameter, set the Design method parameter to Chebyshev Type I.

Passband ripple (dB) — Passband ripple in dB
`1` (default) | positive scalar

Specify the passband ripple of the Chebyshev Type I filter as a positive scalar in dB.

Tunable: Yes

Dependencies

To enable this parameter:

Set the Design method parameter to Chebyshev Type I.
Clear the Specify the passband ripple from input port parameter.

Data Types: single | double

Specify the stopband attenuation from input port — Flag to specify stopband attenuation from input port
`off` (default) | `on`

Select this parameter to specify the stopband attenuation from the input port Ast. When you clear this parameter, you can specify the stopband attenuation in the block dialog box using the Stopband attenuation (dB) parameter.

Dependencies

To enable this parameter, set the Design method parameter to Chebyshev Type II.

Stopband attenuation (dB) — Stopband attenuation in dB
`60` (default) | positive scalar

Specify the stopband attenuation of the Chebyshev Type II filter as a positive scalar in dB.

Tunable: Yes

Dependencies

To enable this parameter:

Set the Design method parameter to Chebyshev Type II.
Clear the Specify the stopband attenuation from input port parameter.

Data Types: single | double

Sample time — Sample time in seconds
`-1` (default) | positive scalar | `Inf`

Specify the sample time as -1 (inherited), Inf (constant sample time), or a positive scalar. This parameter determines when the block produces the output and updates its internal state during simulation. For more details, see What Is Sample Time? (Simulink).

Data Types: single | double

Output data type — Data type of filter coefficients
`double` (default) | `single`

Specify the data type of the filter coefficients that the block outputs through the Num and Den ports. You can set the data type to double or single.

Simulate using — Type of simulation to run
`Interpreted execution` (default) | `Code generation`

Specify the type of simulation to run. You can set this parameter to:

Interpreted execution –– Simulate model using the MATLAB^® interpreter. This option shortens startup time.
Code generation –– Simulate model using generated C code. The first time you run a simulation, Simulink^® generates C code for the block. The C code is reused for subsequent simulations as long as the model does not change. This option requires additional startup time but provides faster subsequent simulations.

Block Characteristics

Data Types	`double` \| `integer` \| `single`
Direct Feedthrough	`no`
Multidimensional Signals	`no`
Variable-Size Signals	`no`
Zero-Crossing Detection	`no`

More About

expand all

Parameter Smoothing

Parameter smoothing gradually changes the values of filter parameters until the desired value is reached.

If you select the Smooth tuned filter parameters check box and update the value of tunable filter parameters during simulation, the block repeatedly redesigns the filter with intermediate values of the parameter until the parameter reaches the desired value. The block uses a first-order IIR filter to smooth the parameter.

$g [n] = α g [n - 1] + (1 - α) t [n],$

where:

g[n] is the instantaneous smoothed parameter
t[n] is the discontinuous target parameter
α is the smoothing factor. When α = 0, no smoothing occurs. As α approaches 1, the number of smoothing operations, and consequently, the number of filter redesigns increase.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

When you generate code from this block, you can tune the filter design specifications in the generated code.

Version History

Introduced in R2023b

expand all

R2024a: Change in the default value of Simulate using parameter

The default value of the Simulate using parameter is now Interpreted execution. With this change, the block uses the MATLAB interpreter for simulation by default.

R2024a: Tunable Lowpass IIR Filter block renamed

The Tunable Lowpass IIR Filter has been renamed as Lowpass IIR Filter Design block.

R2024a: Support for smoothing tunable filter parameters

When tunable filter parameters such as the filter order, cutoff frequency, passband ripple, and stopband attenuation change during simulation, the block can smooth these parameters until the parameters reach the desired value. For more information, see Parameter Smoothing.

Lowpass IIR Filter Design

Description

Examples

Filter Noisy Signal Using Second-Order Section (SOS) Lowpass Filter in Simulink

Ports

Input

N — Filter order positive integer

Dependencies

Fc — 3-dB cutoff frequency positive scalar ≤ 1

Dependencies

Ap — Passband ripple in dB positive scalar

Dependencies

Ast — Stopband attenuation in dB positive scalar

Dependencies

Output

Num — Numerator coefficients P-by-3 matrix

Den — Denominator coefficients P-by-3 matrix

g — Scale values for each second-order section vector

Dependencies

Parameters

Smooth tuned filter parameters — Smooth tuned filter parameters off (default) | on

Smoothing factor — Smoothing factor 0.6 (default) | nonnegative scalar less than 1

Dependencies

Design method — Filter design method Butterworth (default) | Chebyshev Type I | Chebyshev Type II

Specify filter order from input port — Flag to specify filter order from input port off (default) | on

Filter order — Filter order 6 (default) | positive integer

Dependencies

Filter maximum order — Maximum order of filter 10 (default) | positive integer

Design has scale values — Specify if filter has scale values for each section off (default) | on

Specify 3-dB cutoff frequency from input port — Flag to specify 3-dB cutoff frequency from input port off (default) | on

3-dB cutoff frequency — 3-dB cutoff frequency 0.25 (default) | positive scalar ≤ 1

Dependencies

Specify the passband ripple from input port — Flag to specify passband ripple from input port off (default) | on

Dependencies

Passband ripple (dB) — Passband ripple in dB 1 (default) | positive scalar

Dependencies

Specify the stopband attenuation from input port — Flag to specify stopband attenuation from input port off (default) | on

Dependencies

Stopband attenuation (dB) — Stopband attenuation in dB 60 (default) | positive scalar

Dependencies

Sample time — Sample time in seconds -1 (default) | positive scalar | Inf

Output data type — Data type of filter coefficients double (default) | single

Simulate using — Type of simulation to run Interpreted execution (default) | Code generation

Block Characteristics

More About

Parameter Smoothing

Extended Capabilities

C/C++ Code Generation Generate C and C++ code using Simulink® Coder™.

Version History

R2024a: Change in the default value of Simulate using parameter

R2024a: Tunable Lowpass IIR Filter block renamed

R2024a: Support for smoothing tunable filter parameters

See Also

Functions

Blocks

N — Filter order
positive integer

Fc — 3-dB cutoff frequency
positive scalar ≤ 1

Ap — Passband ripple in dB
positive scalar

Ast — Stopband attenuation in dB
positive scalar

Num — Numerator coefficients
P-by-3 matrix

Den — Denominator coefficients
P-by-3 matrix

g — Scale values for each second-order section
vector

Smooth tuned filter parameters — Smooth tuned filter parameters
`off` (default) | `on`

Smoothing factor — Smoothing factor
0.6 (default) | nonnegative scalar less than 1

Design method — Filter design method
`Butterworth` (default) | `Chebyshev Type I` | `Chebyshev Type II`

Specify filter order from input port — Flag to specify filter order from input port
`off` (default) | `on`

Filter order — Filter order
`6` (default) | positive integer

Filter maximum order — Maximum order of filter
`10` (default) | positive integer

Design has scale values — Specify if filter has scale values for each section
`off` (default) | `on`

Specify 3-dB cutoff frequency from input port — Flag to specify 3-dB cutoff frequency from input port
`off` (default) | `on`

3-dB cutoff frequency — 3-dB cutoff frequency
`0.25` (default) | positive scalar ≤ 1

Specify the passband ripple from input port — Flag to specify passband ripple from input port
`off` (default) | `on`

Passband ripple (dB) — Passband ripple in dB
`1` (default) | positive scalar

Specify the stopband attenuation from input port — Flag to specify stopband attenuation from input port
`off` (default) | `on`

Stopband attenuation (dB) — Stopband attenuation in dB
`60` (default) | positive scalar

Sample time — Sample time in seconds
`-1` (default) | positive scalar | `Inf`

Output data type — Data type of filter coefficients
`double` (default) | `single`

Simulate using — Type of simulation to run
`Interpreted execution` (default) | `Code generation`

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.