Bandpass IIR Filter Design
Libraries:
DSP System Toolbox /
Filtering /
Filter Sources
Description
Use the Bandpass IIR Filter Design block to design a bandpass IIR filter using the Butterworth, Chebyshev Type I and Chebyshev Type II design methods. You can tune the filter design specifications such as the filter order, 3-dB cutoff frequencies, passband ripple, and stopband attenuation during simulation. When the values of these parameters change, the block redesigns the filter and outputs the numerator and denominator coefficients in the second-order section (SOS) form (since R2023b) or the fourth-order section (FOS) form.
Examples
Filter a noisy sinusoidal signal using the Fourth-Order Section Filter block. Obtain the numerator and denominator coefficients of the FOS filter using the Bandpass IIR Filter Design block.
Tune the frequency specifications of the FOS filter during simulation.
Open and Run Model
Open the fourthordersectionfilter.slx model.
The input signal in the model is a sum of two sine waves with frequencies of 100 Hz and 350 Hz. The sample rate is 1000 Hz and the number of samples in each frame is 1024. The Random Source block adds zero-mean white Gaussian noise with a variance of 1e-4 to the sum of the sine waves.
The Bandpass IIR Filter Design block designs a sixth-order bandpass IIR filter with the first and second 3-dB cutoff frequencies of 0.25  rad/sample and 0.75
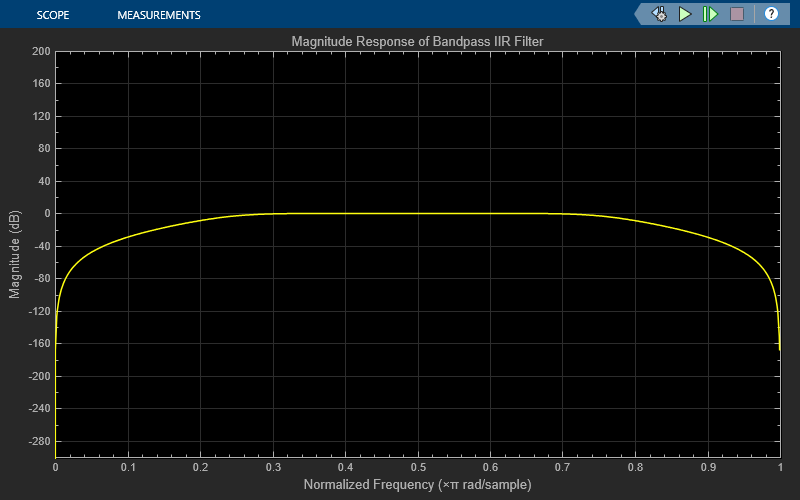
rad/sample and 0.75  rad/sample, respectively. The block generates coefficients as a cascade of fourth-order sections. Visualize the frequency response of the filter using the Filter Visualizer.
rad/sample, respectively. The block generates coefficients as a cascade of fourth-order sections. Visualize the frequency response of the filter using the Filter Visualizer.
Run the model.
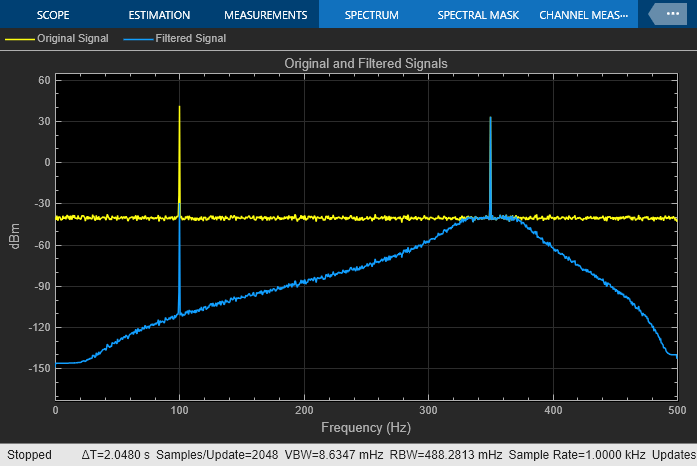
The Fourth-Order Section Filter block filters the noisy sinusoidal signal. Visualize the original sinusoidal signal and the filtered signal using the Spectrum Analyzer.



Tune Frequency Specification of FOS Filter
During simulation, you can tune the frequency specifications of the FOS filter by tuning the frequency parameters in the Bandpass IIR Filter Design block. The frequency response of the FOS filter updates accordingly.
Change the first 3-dB cutoff frequency to 0.65  rad/sample in the Bandpass IIR Filter Design block. The first tone of the sinusoidal signal is attenuated as it no longer falls in the passband region of the filter.
rad/sample in the Bandpass IIR Filter Design block. The first tone of the sinusoidal signal is attenuated as it no longer falls in the passband region of the filter.

Filter a noisy sinusoidal signal using the Second-Order Section Filter block. Obtain the numerator and denominator coefficients of the SOS filter using the Bandpass IIR Filter Design block.
Tune the frequency specifications of the SOS filter during simulation.
Open and Run Model
Open the secondordersectionfilter model.
The input signal in the model is a sum of two sine waves with the frequencies of 100 Hz and 350 Hz. The sample rate is 1000 Hz and the number of samples in each frame is 1024. The Random Source block adds zero-mean white Gaussian noise with a variance of 1e-4 to the sum of the sine waves.
The Bandpass IIR Filter Design block designs a sixth-order bandpass IIR filter with the first and second 3-dB cutoff frequencies of 0.25  rad/sample and 0.75
rad/sample and 0.75  rad/sample, respectively. The block generates coefficients as a cascade of second-order sections. Visualize the frequency response of the filter using the Filter Visualizer.
rad/sample, respectively. The block generates coefficients as a cascade of second-order sections. Visualize the frequency response of the filter using the Filter Visualizer.
Run the model.
The Second-Order Section Filter block filters the noisy sinusoidal signal. Visualize the original sinusoidal signal and the filtered signal using the Spectrum Analyzer.


Tune Frequency Specifications of SOS Filter
During simulation, you can tune the frequency specifications of the SOS filter by tuning the frequency parameters in the Bandpass IIR Filter Design block. The frequency response of the SOS filter updates accordingly.
Change the second 3-dB cutoff frequency to 0.4  rad/sample in the Bandpass IIR Filter Design block. To change the parameter values more gradually during simulation, select the Smooth tuned filter parameters check box and specify a smoothing factor in the Bandpass IIR Filter Design block dialog box. The smoothing factor determines the speed at which the parameter values change until they match the desired new value. If you specify a smoothing factor of 0, the block does not smooth the parameter and immediately sets the parameter to the new value. As the smoothing factor approaches 1, the number of smoothing operations, and consequently, the number of filter redesigns increase. This example uses a smoothing factor is of 0.6.
rad/sample in the Bandpass IIR Filter Design block. To change the parameter values more gradually during simulation, select the Smooth tuned filter parameters check box and specify a smoothing factor in the Bandpass IIR Filter Design block dialog box. The smoothing factor determines the speed at which the parameter values change until they match the desired new value. If you specify a smoothing factor of 0, the block does not smooth the parameter and immediately sets the parameter to the new value. As the smoothing factor approaches 1, the number of smoothing operations, and consequently, the number of filter redesigns increase. This example uses a smoothing factor is of 0.6.
When you change the second 3-dB cutoff frequency to 0.4  rad/sample, the second tone of the sinusoidal signal gets attenuated as it no longer falls in the passband region of the filter.
rad/sample, the second tone of the sinusoidal signal gets attenuated as it no longer falls in the passband region of the filter.


Ports
Input
Specify the filter order as an even positive integer. You can change the filter order you input through this port during simulation.
Dependencies
To enable this port, select the Specify filter order from input port parameter.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Specify the first 3-dB cutoff frequency Fc1 of the filter in normalized frequency units as a nonnegative scalar less than or equal to the second 3-dB cutoff frequency Fc2.
You can change the first 3-dB cut off frequency you input through this port during simulation.
Dependencies
To enable this port, select the Specify first 3-dB cutoff frequency from input port parameter.
Data Types: single | double
Specify the second 3-dB cutoff frequency of the filter in normalized frequency
units as a positive scalar greater than or equal to Fc1 and less
than or equal to 1.
You can change the second 3-dB cut off frequency you input through this port during simulation.
Dependencies
To enable this port, select the Specify second 3-dB cutoff frequency from input port parameter.
Data Types: single | double
Specify the passband ripple of the Chebyshev Type I filter as a nonnegative scalar in dB. You can change the passband ripple you input through this port during simulation.
Dependencies
To enable this port:
Set the Design method parameter to
Chebyshev Type I.Select the Specify the passband ripple from input port parameter.
Data Types: single | double
Specify the stopband attenuation of the Chebyshev Type II filter as a nonnegative scalar in dB. You can change the stopband attenuation you input through this port during simulation.
Dependencies
To enable this port:
Set the Design method parameter to
Chebyshev Type II.Select the Specify the stopband attenuation from input port parameter.
Data Types: single | double
Output
Numerator coefficients, returned as a P-by-3 matrix (SOS form) or a P-by-5 matrix (FOS form), where P is the maximum number of filter sections.
SOS form (since R2023b)
When you set Filter cascade sections form to
Second-order sections, the block generates a
P-by-3 numerator coefficients matrix.
This equation represents the SOS filter in the transfer function form.
where
b is a matrix of numerator coefficients.
a is a matrix of denominator coefficients that the block outputs at the Den output port.
k is the row index.
P equals
ceil(Nmax/2) in the
SOS form, where Nmax is the value of the
Filter maximum order (must be even) parameter.
When the actual filter order N is less than the maximum filter
order Nmax, the last
ceil(Nmax/2) −
ceil(N/2) sections are trivial with
coefficients [b0,
b1,
b2] = [1, 0, 0].
FOS form
When you set Filter cascade sections form to
Fourth-order sections, the block generates a
P-by-5 numerator coefficients matrix.
This equation represents the FOS filter in the transfer function form.
P equals
ceil(Nmax/4) in the
FOS form.
When the actual filter order N is less than the maximum filter
order Nmax, the last
ceil(Nmax/4) −
ceil(N/4) sections are trivial with
coefficients [b0,
b1,
b2,
b3,
b4] = [1, 0, 0, 0, 0].
The data type of this port depends on the value of the Output data type parameter.
Data Types: single | double
Denominator coefficients, returned as a P-by-3 matrix (SOS form) or a P-by-5 matrix (FOS form), where P is the maximum number of filter sections.
SOS form (since R2023b)
When you set Filter cascade sections form to
Second-order sections, the block generates a
P-by-3 denominator coefficients matrix.
This equation represents the SOS filter in the transfer function form.
a is a matrix of denominator coefficients and the leading denominator coefficient a0 is always 1.
b is a matrix of numerator coefficients that the block outputs at the Num port.
k is the row index.
P equals
ceil(Nmax/2) in the
SOS form, where Nmax is the value of the
Filter maximum order (must be even) parameter.
When the actual filter order N is less than the maximum filter
order Nmax, the last
ceil(Nmax/2) −
ceil(N/2) sections are trivial with
coefficients [a0,
a1,
a2] = [1, 0, 0].
FOS form
When you set Filter cascade sections form to
Fourth-order sections, the block generates a
P-by-5 denominator coefficients matrix.
This equation represents the FOS filter in the transfer function form.
P equals
ceil(Nmax/4) in the
FOS form.
The leading denominator coefficient a0 is always 1.
When the actual filter order N is less than the maximum filter
order Nmax, the last
ceil(Nmax/4) −
ceil(N/4) sections are trivial with
coefficients [a0,
a1,
a2,
a3,
a4] = [1, 0, 0, 0, 0].
The data type of this port depends on the value of the Output data type parameter.
Data Types: single | double
Since R2023b
Scale values for each second-order section, returned as a vector with
P + 1 elements, where P is the maximum number
of filter sections and equals
ceil(Nmax/2), where
Nmax is the value of the
Filter maximum order (must be even) parameter.
Tunable: Yes
Dependencies
To enable this port:
Set Filter cascade sections form to
Second-order sections.Select the Design has scale values parameter.
Data Types: single | double
Parameters
Since R2024a
When you select this check box, the block updates the tunable filter parameters such as the filter order, cutoff frequencies, passband ripple, and stopband attenuation gradually by repeatedly designing the filter with intermediate values of the parameter until the parameter reaches the desired value. This process is called parameter smoothing. For more information, see Parameter Smoothing.
When you clear this check box, the block redesigns the filter with the new parameter value immediately.
Since R2024a
Specify the smoothing factor α as a nonnegative scalar less than 1. When α = 0, no smoothing occurs. As α approaches 1, the number of smoothing operations, and consequently, the number of filter redesigns increase.
Tunable: Yes
Dependencies
To enable this parameter, select the Smooth tuned filter parameters parameter.
Specify the filter design method as one of these:
ButterworthChebyshev Type IChebyshev Type II
Select this parameter to specify the filter order from the input port N. When you clear this parameter, you can specify the filter order in the block dialog box using the Filter order (must be even) parameter.
Specify the filter order as an even positive integer less than or equal to the value of the Filter maximum order (must be even) parameter.
Tunable: Yes
Dependencies
To enable this parameter, clear the Specify filter order from input port parameter.
Specify the maximum order of the filter as an even positive integer. The value you specify in the Filter order (must be even) parameter must be less than or equal to the value you specify in the Filter maximum order (must be even) parameter.
Since R2023b
Specify if the filter has scale values for each section. When you select this parameter, the block outputs the scale values through the g output port.
Dependencies
To enable this parameter, set Filter cascade sections form to
Second-order sections.
Select this parameter to specify the first 3-dB filter cutoff frequency from the input port Fc1. When you clear this parameter, you can specify the first 3-dB cutoff frequency in the block dialog box using the First 3-dB cutoff frequency parameter.
Specify the first 3-dB cutoff frequency of the filter in normalized frequency units as a positive scalar less than or equal to the second 3-dB cutoff frequency.
Tunable: Yes
Dependencies
To enable this parameter, clear the Specify first 3-dB cutoff frequency from input port parameter.
Select this parameter to specify the second 3-dB filter cutoff frequency from the input port Fc2. When you clear this parameter, you can specify the second 3-dB cut-off frequency in the block dialog box using the Second 3-dB cutoff frequency parameter.
Specify the second 3-dB cutoff frequency of the filter in normalized frequency units
as a positive scalar greater than or equal to the first 3-dB cutoff frequency and less
than or equal to 1.
Tunable: Yes
Dependencies
To enable this parameter, clear the Specify second 3-dB cutoff frequency from input port parameter.
Select this parameter to specify passband ripple from the input port Ap. When you clear this parameter, you can specify the passband ripple in the block dialog box using the Passband ripple (dB) parameter.
Dependencies
To enable this parameter, set the Design method parameter to
Chebyshev Type I.
Specify the passband ripple of the Chebyshev Type I filter as a positive scalar in dB.
Tunable: Yes
Dependencies
To enable this parameter:
Set the Design method parameter to
Chebyshev Type I.Clear the Specify the passband ripple from input port parameter.
Select this parameter to specify stopband attenuation from the input port Ast. When you clear this parameter, you can specify the stopband attenuation in the block dialog box using the Stopband attenuation (dB) parameter.
Dependencies
To enable this parameter, set the Design method parameter to
Chebyshev Type II.
Specify the stopband attenuation of the Chebyshev Type II filter as a positive scalar in dB.
Tunable: Yes
Dependencies
To enable this parameter:
Set the Design method parameter to
Chebyshev Type II.Clear the Specify the stopband attenuation from input port parameter.
Specify the sample time as -1 (inherited), Inf
(constant sample time), or a positive scalar. This parameter determines when the block
produces the output and updates its internal state during simulation. For more details,
see What Is Sample Time? (Simulink).
Since R2023b
Specify the form of the filter cascade sections as one of these:
Fourth-order sections–– The block generates a P-by-5 matrix of filter coefficients.Second-order sections–– The block generates a P-by-3 matrix of filter coefficients.
Specify the data type of the filter coefficients that the block outputs through the
Num and Den ports. You can set the data type
to double or single.
Specify the type of simulation to run. You can set this parameter to:
Interpreted execution–– Simulate model using the MATLAB® interpreter. This option shortens startup time.Code generation–– Simulate model using generated C code. The first time you run a simulation, Simulink® generates C code for the block. The C code is reused for subsequent simulations as long as the model does not change. This option requires additional startup time but provides faster subsequent simulations.
Block Characteristics
Data Types |
|
Direct Feedthrough |
|
Multidimensional Signals |
|
Variable-Size Signals |
|
Zero-Crossing Detection |
|
More About
Parameter smoothing gradually changes the values of filter parameters until the desired value is reached.
If you select the Smooth tuned filter parameters check box and update the value of tunable filter parameters during simulation, the block repeatedly redesigns the filter with intermediate values of the parameter until the parameter reaches the desired value. The block uses a first-order IIR filter to smooth the parameter.
where:
g[n] is the instantaneous smoothed parameter
t[n] is the discontinuous target parameter
α is the smoothing factor. When α = 0, no smoothing occurs. As α approaches 1, the number of smoothing operations, and consequently, the number of filter redesigns increase.
References
[1] Orfanidis, Sophocles J. Introduction to Signal Processing. Prentice Hall, 1996.
Extended Capabilities
When you generate code from this block, you can tune the filter design specifications in the generated code.
Version History
Introduced in R2023aThe default value of the Simulate using parameter is now
Interpreted execution. With this change, the block uses the
MATLAB interpreter for simulation by default.
The Tunable Bandpass IIR Filter has been renamed as Bandpass IIR Filter Design block.
When tunable filter parameters such as the filter order, cutoff frequencies, passband ripple, and stopband attenuation change during simulation, the block can smooth these parameters until the parameters reach the desired value. For more information, see Parameter Smoothing.
Starting in R2023b, the Tunable Bandpass IIR Filter block generates filter coefficients in the SOS or FOS form. You can specify the form using the new Filter cascade sections form parameter.
When you set Filter cascade sections form to Second-order
sections and select Design has scale values, the block
outputs scale values through the g port.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
选择网站
选择网站以获取翻译的可用内容,以及查看当地活动和优惠。根据您的位置,我们建议您选择:。
您也可以从以下列表中选择网站:
如何获得最佳网站性能
选择中国网站(中文或英文)以获得最佳网站性能。其他 MathWorks 国家/地区网站并未针对您所在位置的访问进行优化。
美洲
- América Latina (Español)
- Canada (English)
- United States (English)
欧洲
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)