bssm
Description
bssm creates a bssm object, representing a Bayesian linear state-space model,
from a specified parameter-to-matrix mapping function, which defines the state-space model
structure, and the log prior distribution function of the parameters. The state-space model
can be time-invariant or time-varying (see Decide on Model Structure), and the state or observation
variables, xt or
yt, respectively, can be multivariate
series.
In general, a bssm object specifies the joint prior distribution and
characteristics of the state-space model only. That is, the model object is a template
intended for further use. Specifically, to incorporate data into the model for posterior
distribution analysis, pass the model object and data to the appropriate object function.
Alternative state-space models include:
Creation
Syntax
Description
There are several ways to create a bssm object representing a Bayesian
state-space model:
Create Prior Model — Directly create a
bssmobject, representing a prior model, by using thebssmfunction and specifying the parameter-to-matrix mapping function and log prior distribution function of the parameters. This method accommodates simple through complex state-space model structures. For more details, see the following syntax.Convert Standard Model to Bayesian Prior Model — Convert a specified standard, linear state-space model, an
ssmobject, to abssmobject by passing the model to thessm2bssmfunction. The converted Bayesian model has the same state-space structure as the standard model. Use this method for simple state-space models when you prefer to specify the coefficient matrices explicitly. You can optionally specify the log prior density of the parameters. For details, seessm2bssmandssm.Estimate Posterior Model — Pass a
bssmobject representing a prior model, observed response data, and initial parameter values to theestimatefunction to obtain abssmobject representing a posterior model. For more details, seeestimate.
PriorMdl = bssm(ParamMap,ParamDistribution)PriorMdl, representing a prior model with Gaussian state
disturbances and observation innovations, using the parameter-to-matrix mapping function
ParamMap, which you write, and the log prior distribution of the
parameters.
The ParamMap function maps the collection of linear state-space
model parameters Θ to the time-invariant or time-varying coefficient matrices
A, B, C, and
D. In addition to the coefficient matrices,
ParamMap can optionally map any of the following quantities:
Initial state means and covariances
Mean0andCov0State types
StateTypeDeflated observation data
DeflatedDatato accommodate a regression component in the observation equation
The ParamDistribution function accepts Θ and returns the
corresponding log density.
PriorMdl is a template that specifies the joint prior distribution
of Θ and the structure of the state-space model.
PriorMdl = bssm(ParamMap,ParamDistribution,Name=Value)bssm(ParamMap,ParamDistribution,ObservationDistribution=struct("Name","t","DoF",6))
specifies t distribution with 6 degrees of freedom for all observation
innovation variables ut in the Bayesian
state-space model.
Input Arguments
Parameter-to-matrix mapping function that determines the data likelihood,
specified as a function handle in the form
@, where
fcnNamefcnNameParamMap sets the ParamMap property. Object
functions of bssm compute the data likelihood by using the standard Kalman filter, where probabilities additionally condition on the
parameters.
Suppose paramMapparamMap
function [A,B,C,D,Mean0,Cov0,StateType,DeflateY] = paramMap(theta,...otherInputs...) ... end
thetanumParams-by-1 numeric vector of the linear state-space model parameters Θ as the first input argument. The function can accept other inputs in subsequent positions.ParamMapreturns the state-space model parameters in this table.Quantity Output Position Description At 1 Required state-transition coefficient matrix
ABt 2 Required state-disturbance-loading coefficient matrix
BCt 3 Required measurement-sensitivity coefficient matrix
CDt 4 Required observation-innovation coefficient matrix
Dμ0 5 Optional initial state mean vector
Mean0Σ0 6 Optional initial state covariance matrix
Cov0StateType7 Optional state classification vector, either stationary (
0), the constant 1 (1), or diffuse, static, or nonstationary (2)DeflatedData8 Optional array of response data deflated by predictor data, which accommodates a regression component in the observation equation
The subscript t indicates that the parameters can be time-varying (ignore the subscript for time-invariant parameters).
To skip specifying an optional output argument, set the argument to
[]in the function body. For example, to skip specifyingMean0, setMean0 = [];in the function.For the default values of
Mean0,Cov0, andStateType, see Algorithms.
Specify parameters to include in the posterior distribution by setting their value
to an entry in the first input argument
theta
A = theta(1); B = theta(2); C = 1; D = theta(3);
If paramMapbssm object by
calling:
Mdl = bssm(@paramMap,...)
In general, create the bssm object by calling:
Mdl = bssm(@(theta)paramMap(theta,...otherInputArgs...),...)
Example: bssm(@(params)
specifies the parameter-to-matrix mapping function
paramFun(theta,y,z),@ParamDistribution)paramFuntheta, observed responses
y, and predictor data z.
Tip
A best practice is to set StateType of each state within
ParamMap for both of the following reasons:
By default, the software generates
StateType, but the default choice might not be accurate. For example, the software cannot distinguish between a constant 1 state and a static state.The software cannot infer
StateTypefrom data because the data theoretically comes from the observation equation. The realizations of the state equation are unobservable.
Data Types: function_handle
Log of joint probability density function of the state-space model parameters
Π(Θ), specified as a function handle in the form
@, where
fcnNamefcnNameParamDistribution sets the ParamDistribution
property.
Suppose logPriorlogPrior
function logpdf = logPrior(theta,...otherInputs...) ... end
thetanumParams-by-1 numeric vector of the linear state-space model parameters Θ. Elements ofthetaParamMap. The function can accept other inputs in subsequent positions.logpdftheta
If ParamDistribution requires the input parameter vector
argument only, you can create the bssm object by calling:
Mdl = bssm(...,@logPrior)
In general, create the bssm object by calling:
Mdl = bssm(...,@(theta)logPrior(theta,...otherInputArgs...))
Tip
Because out-of-bounds prior density evaluation is 0, set the log prior density
of out-of-bounds parameter arguments to -Inf.
Data Types: function_handle
Properties
Parameter-to-matrix mapping function, stored as a function handle and set by the
ParamMap input argument. ParamMap completely
specifies the structure of the state-space model.
Data Types: function_handle
Parameter distribution representation, stored as a function handle or a
numParams-by-numDraws numeric matrix.
ParamDistributionis a function handle for the log prior distribution of the parametersParamDistributionwhen you createPriorMdldirectly by usingbssmor when you convert a standard state-space model by usingssm2bssm.ParamDistributionis anumParams-by-numDrawsnumeric matrix containing random draws from the posterior distribution of the parameters when you estimate the posterior by usingestimate. Rows correspond to the elements oftheta
Data Types: function_handle
Since R2022b
Distribution of the state disturbance process, specified as a distribution name or
structure array in this table. bssm stores the value as a
structure array.
| Distribution | Name | Variable Support | Structure Array | Hyperparameter Estimation Support |
|---|---|---|---|---|
| Standard Gaussian | "Gaussian" | Multivariate | struct("Name","Gaussian") | Not applicable |
| Student’s t | "t" | Multivariate | struct("Name","t","DoF", | Yes |
The specified distribution applies to all state disturbance process variables.
For the Student's t distribution:
If you supply a structure array, you must specify both the
"Name"and"DoF"fields.You can change the hyperparameter value by using dot notation after you create the model. For example,
Mdl.Distribution.DoF = 3.To facilitate posterior sampling,
bssmrepresents multivariate Student's t-distributed variables as an inverse-gamma scale mixture. For more details, see Latent Variance Variables of t-Distributed Errors.
For more details on distribution hyperparameters, see Distribution Hyperparameters.
Example: struct("Name","t","DoF",6) specifies a
t distribution with 6 degrees of freedom for the
state disturbance process.
Since R2022b
Distribution of the observation innovation process, specified as a distribution name
or structure array in this table. bssm stores the value as a
structure array.
| Distribution | Name | Variable Support | Structure Array | Hyperparameter Estimation Support |
|---|---|---|---|---|
| Standard Gaussian | "Gaussian" | Multivariate | struct("Name","Gaussian") | Not applicable |
| Student’s t | "t" | Multivariate | struct("Name","t","DoF", | Yes |
| Finite Gaussian mixture | "mixture" | Univariate | struct("Name","mixture","Weight", | No |
| Laplace | "Laplace" | Univariate | struct("Name","Laplace") | Not applicable |
| Skew normal | "skewnormal" | Univariate | struct("Name","skewnormal","Delta", | Yes |
The specified distribution applies to all observation innovation process variables. However, you can specify different Gaussian mixture regime means and variances among the variables.
For the Student's t distribution:
If you supply a structure array, you must specify both the
"Name"and"DoF"fields.You can change the hyperparameter value by using dot notation after you create the model. For example,
Mdl.Distribution.DoF = 3.To facilitate posterior sampling,
bssmrepresents multivariate Student's t-distributed variables as an inverse-gamma scale mixture. For more details, see Latent Variance Variables of t-Distributed Errors.
For the finite Gaussian mixture distribution,
bssmsets the number of regimes (mixture components) to the number of elements ofweightweight
For more details on distribution hyperparameters, see Distribution Hyperparameters.
Example: struct("Name","t","DoF",6) specifies a
t distribution with 6 degrees of freedom for the
state disturbance process.
Example: struct("Name","mixture","Mean",[-1 1],"Weight",[0.6 0.4])
specifies a two-regime Gaussian mixture model for the univariate observation innovation
variable. The regime weights are 0.6 and 0.4. The
regime mean vector is [-1 1]. The default variance for all regimes is
1.
Object Functions
Examples
Create a Bayesian state-space model containing two independent, stationary, autoregressive states. The observations are the deterministic sum of the two states (in other words, the model does not impose observation errors ). Symbolically, the system of equations is
Arbitrarily assume that the prior distribution of , , , and are independent Gaussian random variables with mean 0.5 and variance 1.
The Local Functions section contains two functions required to specify the Bayesian state-space model. You can use the functions only within this script.
The paramMap function accepts a vector of the unknown state-space model parameters and returns all of the following quantities:
A= .B= .C= .D= 0.Mean0andCov0are empty arrays[], which specify the defaults.StateType= , indicating that each state is stationary.
The paramDistribution function accepts the same vector of unknown parameters as does paramMap, but it returns the log prior density of the parameters at their current values. Specify that parameter values outside the parameter space have log prior density of -Inf.
Create the Bayesian state-space model by passing function handles directly to paramMap and paramDistribution to bssm.
Mdl = bssm(@paramMap,@priorDistribution)
Mdl =
Mapping that defines a state-space model:
@paramMap
Log density of parameter prior distribution:
@priorDistribution
Mdl is a bssm model specifying the state-space model structure and prior distribution of the state-space model parameters. Because Mdl contains unknown values, it serves as a template for posterior estimation.
Local Functions
This example uses the following functions. paramMap is the parameter-to-matrix mapping function and priorDistribution is the log prior distribution of the parameters.
function [A,B,C,D,Mean0,Cov0,StateType] = paramMap(theta) A = [theta(1) 0; 0 theta(2)]; B = [theta(3) 0; 0 theta(4)]; C = [1 1]; D = 0; Mean0 = []; % MATLAB uses default initial state mean Cov0 = []; % MATLAB uses initial state covariances StateType = [0; 0]; % Two stationary states end function logprior = priorDistribution(theta) paramconstraints = [(abs(theta(1)) >= 1) (abs(theta(2)) >= 1) ... (theta(3) < 0) (theta(4) < 0)]; if(sum(paramconstraints)) logprior = -Inf; else mu0 = 0.5*ones(numel(theta),1); sigma0 = 1; p = normpdf(theta,mu0,sigma0); logprior = sum(log(p)); end end
Create a time-varying, Bayesian state-space model with these characteristics:
From periods 1 through 250, the state equation includes stationary AR(2) and MA(1) models, respectively, and the observation model is the weighted sum of the two states.
From periods 251 through 500, the state model includes only the first AR(2) model.
and is the identity matrix.
The prior density is flat.
Symbolically, the state-space model is
Write a function that specifies how the parameters theta map to the state-space model matrices, the initial state moments, and the state types. Save this code as a file named timeVariantParamMap.m on your MATLAB® path. Alternatively, open the example to access the function.
function [A,B,C,D,Mean0,Cov0,StateType] = timeVariantParamMapBayes(theta,T) % Time-variant, Bayesian state-space model parameter mapping function % example. This function maps the vector params to the state-space matrices % (A, B, C, and D), the initial state value and the initial state variance % (Mean0 and Cov0), and the type of state (StateType). From periods 1 % through T/2, the state model is a stationary AR(2) and an MA(1) model, % and the observation model is the weighted sum of the two states. From % periods T/2 + 1 through T, the state model is the AR(2) model only. The % log prior distribution enforces parameter constraints (see % flatPriorBSSM.m). T1 = floor(T/2); T2 = T - T1 - 1; A1 = {[theta(1) theta(2) 0 0; 1 0 0 0; 0 0 0 theta(4); 0 0 0 0]}; B1 = {[theta(3) 0; 0 0; 0 1; 0 1]}; C1 = {theta(5)*[1 0 1 0]}; D1 = {theta(6)}; Mean0 = [0.5 0.5 0 0]; Cov0 = eye(4); StateType = [0 0 0 0]; A2 = {[theta(1) theta(2) 0 0; 1 0 0 0]}; B2 = {[theta(3); 0]}; A3 = {[theta(1) theta(2); 1 0]}; B3 = {[theta(3); 0]}; C3 = {theta(7)*[1 0]}; D3 = {theta(8)}; A = [repmat(A1,T1,1); A2; repmat(A3,T2,1)]; B = [repmat(B1,T1,1); B2; repmat(B3,T2,1)]; C = [repmat(C1,T1,1); repmat(C3,T2+1,1)]; D = [repmat(D1,T1,1); repmat(D3,T2+1,1)]; end
Write a function that specifies a joint flat prior and parameter constraints. Save this code as a file named flatPriorBSSM.m on your MATLAB path. Alternatively, open the example to access the function.
function logprior = flatPriorBSSM(theta) % flatPriorBSSM computes the log of the flat prior density for the eight % variables in theta (see timeVariantParamMapBayes.m). Log probabilities % for parameters outside the parameter space are -Inf. % theta(1) and theta(2) are lag 1 and lag 2 terms in a stationary AR(2) % model. The eigenvalues of the AR(1) representation need to be within % the unit circle. evalsAR2 = eig([theta(1) theta(2); 1 0]); evalsOutUC = sum(abs(evalsAR2) >= 1) > 0; % Standard deviations of disturbances and errors (theta(3), theta(6), % and theta(8)) need to be positive. nonnegsig1 = theta(3) <= 0; nonnegsig2 = theta(6) <= 0; nonnegsig3 = theta(8) <= 0; paramconstraints = [evalsOutUC nonnegsig1 ... nonnegsig2 nonnegsig3]; if sum(paramconstraints) > 0 logprior = -Inf; else logprior = 0; % Prior density is proportional to 1 for all values % in the parameter space. end end
Create a bssm object representing the Bayesian state-space model object. Supply the parameter-to-matrix mapping function timeVariantParamMapBayes as a function handle of solely theta by setting the time series length to 500.
numObs = 500; Mdl = bssm(@(theta)timeVariantParamMapBayes(theta,numObs),@flatPriorBSSM)
Mdl =
Mapping that defines a state-space model:
@(theta)timeVariantParamMapBayes(theta,numObs)
Log density of parameter prior distribution:
@flatPriorBSSM
This example shows how to specify that the state disturbances of a Bayesian state-space model are Student's t distributed in order to model excess kurtosis in the state equation. The example shows how to prepare the degrees of freedom parameter for posterior estimation and the example fully specifies the distribution.
Consider the Bayesian state-space model in Create Time-Invariant Bayesian State-Space Model with Known and Unknown Parameters, but assume that the state disturbances are distributed as a Student's random variable.
Create the model by passing function handles to the local functions that represent the state-space model structure and prior distribution of the model parameters . Specify that the distribution of the state disturbances is Student's .
Mdl = bssm(@paramMap,@priorDistribution,StateDistribution="t");
Mdl.StateDistributionans = struct with fields:
Name: "t"
DoF: NaN
Mdl is a bssm model. The property Mdl.StateDistribution is a structure array specifying the distribution of the state disturbances. The field DoF is NaN by default, which means that the -distribution degrees of freedom is configured for estimation with all unknown state-space model parameters .
You can specify a fixed value for the degrees of freedom two ways:
By setting the DoF field to the positive scalar using dot notation
By recreating the
bssmmodel and supplying a structure array specifying the distribution name and degrees of freedom
Specify that the degrees of freedom is 6 by using both methods.
Mdl.StateDistribution.DoF = 6
Mdl =
Mapping that defines a state-space model:
@paramMap
Log density of parameter prior distribution:
@priorDistribution
Degree of freedom of t distribution in the state equation:
6
statedist = struct("Name","t","DoF",6); Mdl2 = bssm(@paramMap,@priorDistribution,StateDistribution=statedist)
Mdl2 =
Mapping that defines a state-space model:
@paramMap
Log density of parameter prior distribution:
@priorDistribution
Degree of freedom of t distribution in the state equation:
6
Mdl and Mdl2 are equal.
Local Functions
function [A,B,C,D,Mean0,Cov0,StateType] = paramMap(theta) A = [theta(1) 0; 0 theta(2)]; B = [theta(3) 0; 0 theta(4)]; C = [1 1]; D = 0; Mean0 = []; % MATLAB uses default initial state mean Cov0 = []; % MATLAB uses initial state covariances StateType = [0; 0]; % Two stationary states end function logprior = priorDistribution(theta) paramconstraints = [(abs(theta(1)) >= 1) (abs(theta(2)) >= 1) ... (theta(3) < 0) (theta(4) < 0)]; if(sum(paramconstraints)) logprior = -Inf; else mu0 = 0.5*ones(numel(theta),1); sigma0 = 1; p = normpdf(theta,mu0,sigma0); logprior = sum(log(p)); end end
To model volatility clustering, you can specify distributed observation innovations by setting appropriate mixture weights, and regime means and variances of a 7-regime Gaussian mixture distribution.
Consider the Bayesian state-space model in Create Time-Invariant Bayesian State-Space Model with Known and Unknown Parameters, but assume that the observation-innovations process is distributed as a random variable.
Create a structure array with the following fields and values.
Field
Namewith value"mixture"Field
Weightwith value[0.0089 0.0541 0.1338 0.2761 0.2923 0.1494 0.0854]Field
Meanwith value[-9.3202 -5.3145 -3.4147 -1.7097 -0.4531 0.3975 1.1925]Field
Variancewith value[3.2793 2.4574 1.8874 1.3121 0.8843 0.5898 0.4995].^2
weight = [0.0089 0.0541 0.1338 0.2761 0.2923 0.1494 0.0854]; mu = [-9.3202 -5.3145 -3.4147 -1.7097 -0.4531 0.3975 1.1925]; sigma2 = [3.2793 2.4574 1.8874 1.3121 0.8843 0.5898 0.4995].^2; ObsInnovDist = struct("Name","mixture","Weight",weight, ... "Mean",mu,"Variance",sigma2);
Create the model by passing function handles to the local functions that represent the state-space model structure and prior distribution of the model parameters . Use the structure array ObsInnovDist to specify that the distribution of the observation innovations is finite Gaussian mixture with hyperparameters that define a distribution.
Mdl = bssm(@paramMap,@priorDistribution,ObservationDistribution=ObsInnovDist); Mdl.ObservationDistribution
ans = struct with fields:
Name: "mixture"
Weight: [0.0089 0.0541 0.1338 0.2761 0.2923 0.1494 0.0854]
Mean: [-9.3202 -5.3145 -3.4147 -1.7097 -0.4531 0.3975 1.1925]
Variance: [10.7538 6.0388 3.5623 1.7216 0.7820 0.3479 0.2495]
Mdl is a bssm model. The property Mdl.ObservationDistribution is a structure array specifying the distribution of the observation-innovations process. All distribution hyperparameters are fully specified.
Plot the distribution of the observation innovations. Compare the Gaussian mixture representation of the and the true distributions.
r = numel(weight); LogChi2GMMdl = gmdistribution(mu',reshape(sigma2,1,1,r),weight); gmPDF = @(x)arrayfun(@(x0)pdf(LogChi2GMMdl,x0),x); logchi2PDF = @(x)((1/sqrt(2*pi))*exp((x-exp(x))/2)); figure fplot(gmPDF,[-10,5]) hold on fplot(logchi2PDF,"--r") title("Log Chi-Squared Distribution: Gaussian Mixture Versus True") legend("Gaussian Mixture","True",Location="best")
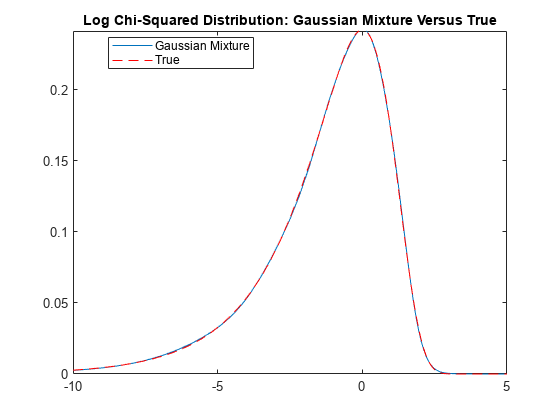
The distributions appear nearly identical.
Local Functions
function [A,B,C,D,Mean0,Cov0,StateType] = paramMap(theta) A = [theta(1) 0; 0 theta(2)]; B = [theta(3) 0; 0 theta(4)]; C = [1 1]; D = 0; Mean0 = []; % MATLAB uses default initial state mean Cov0 = []; % MATLAB uses initial state covariances StateType = [0; 0]; % Two stationary states end function logprior = priorDistribution(theta) paramconstraints = [(abs(theta(1)) >= 1) (abs(theta(2)) >= 1) ... (theta(3) < 0) (theta(4) < 0)]; if(sum(paramconstraints)) logprior = -Inf; else mu0 = 0.5*ones(numel(theta),1); sigma0 = 1; p = normpdf(theta,mu0,sigma0); logprior = sum(log(p)); end end
Consider a regression of the US unemployment rate onto and real gross national product (RGNP) rate, and suppose the resulting innovations are an ARMA(1,1) process. The state-space form of the relationship is
where:
is the ARMA process.
is a dummy state for the MA(1) effect.
is the observed unemployment rate deflated by a constant and the RGNP rate ().
is an iid Gaussian series with mean 0 and standard deviation 1.
Load the Nelson-Plosser data set, which contains a table DataTable that has the unemployment rate and RGNP series, among other series.
load Data_NelsonPlosserCreate a variable in DataTable that represents the returns of the raw RGNP series. Because price-to-returns conversion reduces the sample size by one, prepad the series with NaN.
DataTable.RGNPRate = [NaN; price2ret(DataTable.GNPR)]; T = height(DataTable);
Create variables for the regression. Represent the unemployment rate as the observation series and the constant and RGNP rate series as the deflation data .
Z = [ones(T,1) DataTable.RGNPRate]; y = DataTable.UR;
Write a function that specifies how the parameters theta map to the state-space model matrices, defers the initial state moments to the default, specifies the state types, and specifies the regression. Save this code as a file named armaDeflateYBayes.m on your MATLAB® path. Alternatively, open this example to access the function.
function [A,B,C,D,Mean0,Cov0,StateType,DeflatedY] = armaDeflateYBayes(theta,y,Z) % Time-invariant, Bayesian state-space model parameter mapping function % example. This function maps the vector parameters to the state-space % matrices (A, B, C, and D), the default initial state value and the % default initial state variance (Mean0 and Cov0), the type of state % (StateType), and the deflated observations (DeflatedY). The log prior % distribution enforces parameter constraints (see flatPriorDeflateY.m). A = [theta(1) theta(2); 0 0]; B = [1; 1]; C = [theta(3) 0]; D = 0; Mean0 = []; Cov0 = []; StateType = [0 0]; DeflatedY = y - Z*[theta(4); theta(5)]; end
Write a function that specifies a joint flat prior and parameter constraints. Save this code as a file named flatPriorDeflateY.m on your MATLAB path. Alternatively, open this example to access the function.
% Copyright 2022 The MathWorks, Inc. function logprior = flatPriorDeflateY(theta) % flatPriorDeflateY computes the log of the flat prior density for the five % variables in theta (see armaDeflateYBayes.m). Log probabilities % for parameters outside the parameter space are -Inf. % theta(1) and theta(2) are the AR and MA terms in a stationary % ARMA(1,1) model. The AR term must be within the unit circle. AROutUC = abs(theta(1)) >= 1; % The standard deviation of innovations (theta(3)) must be positive. nonnegsig1 = theta(3) <= 0; paramconstraints = [AROutUC nonnegsig1]; if sum(paramconstraints) > 0 logprior = -Inf; else logprior = 0; % Prior density is proportional to 1 for all values % in the parameter space. end end
Create a bssm object representing the Bayesian state-space model. Specify the parameter-to-matrix mapping function as a handle to a function solely of the parameters theta.
Mdl = bssm(@(theta)armaDeflateYBayes(theta,y,Z),@flatPriorDeflateY)
Mdl =
Mapping that defines a state-space model:
@(theta)armaDeflateYBayes(theta,y,Z)
Log density of parameter prior distribution:
@flatPriorDeflateY
More About
A Bayesian linear state-space model is a Bayesian view of a standard linear state-space model, in which the vector of model parameters Θ are treated as random variables with a joint prior distribution Π(Θ) and a posterior distribution composed of the joint prior and data likelihood computed by the standard Kalman filter Π(Θ|yt).
In general, a linear, multivariate, time-varying, Gaussian state-space model is the system of equations
for t = 1, ..., T and where:
is an mt-dimensional state vector describing the dynamics of some, possibly unobservable, phenomenon at period t. The initial state distribution (x0) has mean μ0 (
Mean0) and covariance matrix Σ0 (Cov0).is an nt-dimensional observation vector describing how the states are measured by observers at period t.
is a kt-dimensional white-noise vector of state disturbances at period t. All disturbances are either multivariate Gaussian distributed or multivariate Student's t distributed, with νu degrees of freedom.
is an ht-dimensional white-noise vector of observation innovations at period t. All innovations are either multivariate Gaussian or Student's t distributed, or univariate finite Gaussian mixture, Laplace, or skew normal distributed.
εt and ut are uncorrelated.
For time-invariant state-space models,
is row t of a T-by-d matrix of predictors Z. Each column of Z corresponds to a predictor, and each successive row to a successive period. If the observations are multivariate, then all predictors deflate each observation.
β is a d-by-n matrix of regression coefficients for Zt.
At, Bt, Ct, Dt, and β (when present) are model parameters arbitrarily collected in the vector Θ. The joint prior distribution of Θ is Π(Θ) and the joint posterior distribution of Θ is Π(Θ|yt,Zt).
The following definitions describe each of the model parameters and state
characteristics, and how to configure them as outputs of
ParamMap.
The state-transition coefficient matrix At is a matrix or cell vector of matrices that specifies how the states xt are expected to transition from period t – 1 to t, for all t = 1,...,T. In other words, the expected state-transition equation at period t is E(xt|xt–1) = Atxt–1.
For time-invariant state-space models, the output A is an
m-by-m matrix, where m is the
number of state variables.
For time-varying state-space models, the output A is a series of
matrices represented by a T-dimensional cell array, where
A{t} contains an
mt-by-mt
– 1 state-transition coefficient matrix. If the number of state variables
changes from period t – 1 to t,
mt ≠
mt – 1.
The state-disturbance-loading coefficient matrix Bt is a matrix or cell vector of matrices that specifies the additive error structure of the state disturbances ut in the state-transition equation from period t – 1 to t, for all t = 1,...,T. In other words, the state-transition equation at period t is xt = Atxt–1 + Btut.
For time-invariant state-space models, the output B is an m-by-k matrix, where m is the number of state variables and k is the number of state disturbances. The quantity B*(B') is the state-disturbance covariance matrix for all periods.
For time-varying state-space models, B is a T-dimensional cell array, where B{t} contains an mt-by-kt state-disturbance-loading coefficient matrix. If the number of state variables or state disturbances changes at period t, the matrix dimensions between B{t-1} and B{t} vary. The quantity B{t}*(B{t}') is the state-disturbance covariance matrix for period t.
The measurement-sensitivity coefficient matrix Ct is a matrix or cell vector of matrices that specifies how the states xt are expected to linearly combine at period t to form the observations, yt, for all t = 1,...,T. In other words, the expected observation equation at period t is E(yt|xt) = Ctxt.
For time-invariant state-space models, the output C is an
n-by-m matrix, where n is the
number of observation variables and m is the number of state
variables.
For time-varying state-space models, the output C is a
T-dimensional cell array, where C{t} contains an
nt-by-mt
measurement-sensitivity coefficient matrix. If the number of state or observation
variables changes at period t, the matrix dimensions between
C{t-1} and C{t} vary.
The observation-innovation coefficient matrix Dt is a matrix or cell vector of matrices that specifies the additive error structure of the observation innovations εt in the observation equation at period t, for all t = 1,...,T. In other words, the observation equation at period t is yt = Ctxt + Dtεt.
For time-invariant state-space models, the output D is an n-by-h matrix, where n is the number of observation variables and h is the number of observation innovations. The quantity D*(D') is the observation-innovation covariance matrix for all periods.
For time-varying state-space models, the output D is a T-dimensional cell array, where D{t} contains an nt-by-ht matrix. If the number of observation variables or observation innovations changes at period t, then the matrix dimensions between D{t-1} and D{t} vary. The quantity D{t}*(D{t}') is the observation-innovation covariance matrix for period t.
Other state characteristics include initial state moments and a description of the dynamic behavior of each state.
You can optionally specify the state characteristics by including extra output arguments
for ParamMap after the required coefficient matrices.
Mean0— Initial state mean μ0, an m-by-1 numeric vector, where m is the number of states in x1.Cov0— Initial state covariance matrix Σ0, an m-by-m positive semidefinite matrix.StateType— State dynamic behavior indicator, an m-by-1 numeric vector. This table summarizes the available types of initial state distributions.Value State Dynamic Behavior Indicator 0Stationary (for example, ARMA models) 1The constant 1 (that is, the state is 1 with probability 1) 2Diffuse, nonstationary (for example, random walk model, seasonal linear time series), or static state For example, suppose that the state equation has two state variables: The first state variable is an AR(1) process, and the second state variable is a random walk. Specify the initial distribution types by setting
StateType=[0; 2];within theParamMapfunction.
A static state does not change in value throughout the sample, that is, for all t = 1,...,T.
To facilitate posterior sampling, multivariate Student's t-distributed state disturbances and observation innovations are each represented as an inverse-gamma scale mixture, where the inverse-gamma random variable is the latent variance variable.
Explicitly, suppose the m-dimensional state disturbances ut are iid multivariate t distributed with location 0, scale Im, and degrees of freedom νu. As an inverse-gamma scale mixture
where:
The latent variable ζt is inverse-gamma with shape and scale νu/2.
is an m-dimensional multivariate standard Gaussian random variable.
Multivariate t-distributed observation innovations can be similarly decomposed.
You can access ζt by writing a custom output
function that returns the field for the specified error type, either
StateVariance or ObservationVariance. For more
details, see the OutputFunction name-value argument and
Output output argument.
Tips
Load the data to the MATLAB workspace before creating the model.
Create the parameter-to-matrix mapping function and log prior distribution function each as their own file.
To specify a log χ21 distribution for the observation innovation process εt, set the
ObservationDistributionto the structure arraystruct("Weight",, where:weight,"Mean",mu,"Variance",sigma2)weight[0.0089 0.0541 0.1338 0.2761 0.2923 0.1494 0.0854].mu[-9.3202 -5.3145 -3.4147 -1.7097 -0.4531 0.3975 1.1925].sigma2[3.2793 2.4574 1.8874 1.3121 0.8843 0.5898 0.4995].^2.
Algorithms
This table describes the supported distribution hyperparameters, and their values and defaults.
| Distribution | Error Support | Hyperparameter | Field Name | Value | Default |
|---|---|---|---|---|---|
| Student's t | Multivariate ut (state) and εt (observation) | Degrees of freedom parameter | "DoF" | Positive numeric scalar, NaN, or a function handle. You
must specify the value. | When you specify a structure array, you must specify
"DoF". Otherwise, the default is
NaN. |
| Finite Gaussian mixture | Univariate εt | Weights (probability distribution) for r regimes | "Weight" | Length r nonnegative vector.
| 1 |
| Means for r regimes | "Mean" | Length r finite numeric row vector | zeros(1, | ||
| Variances for r regimes | "Variance" | Length r finite numeric row vector | ones(1, | ||
| Skew normal | Univariate εt | Distribution scale is and shape is δ | "Delta" | Numeric scalar or NaN | NaN |
bssmfixes hyperparameters to specified numeric values.For a
NaNor a function handle, where the values are supported,bssmtreats the hyperparameter as unknown. Consequently,bssmobject functions estimate them by computing their posterior distribution with all other unknown parameters in Θ. The value of the hyperparameter determines its prior distribution.For
NaN, the prior is flat.For a function handle (supported for
"DoF"), the associated function represents the log prior distribution. The function has the form, wherexFor example, a valid function handle isfunction logpdf = logPrior(x,...otherInputs...) ... end
@(x)log(normpdf(x,7,1)).
For each state variable
jMean0andCov0depend onStateType(:j)If
StateType((stationary state),j) = 0bssmgenerates the initial value using the stationary distribution. If you provide all values in the coefficient matrices (that is, your model has no unknown parameters),bssmgenerates the initial values. Otherwise, the software generates the initial values during estimation.If
StateType((constant state),j) = 1Mean0(isj)1andCov0(isj)0.If
StateType((nonstationary or diffuse state),j) = 2Mean0(is 0 andj)Cov0(isj)1e7.
For static states that do not equal 1 throughout the sample, the software cannot assign a value to the degenerate, initial state distribution. Therefore, set the
StateTypeof static states to2. Consequently, the software treats static states as nonstationary and assigns the static state a diffuse initial distribution.bssmmodels do not store observed responses or predictor data. Supply the data wherever necessary using the appropriate input or name-value pair arguments.DeflateYis the deflated-observation data, which accommodates a regression component in the observation equation. For example, in this function, which has a linear regression component,Yis the vector of observed responses andZis the vector of predictor data.function [A,B,C,D,Mean0,Cov0,StateType,DeflateY] = ParamFun(theta,Y,Z) ... DeflateY = Y - params(9) - params(10)*Z; ... end
References
[1] Hastings, Wilfred K. "Monte Carlo Sampling Methods Using Markov Chains and Their Applications." Biometrika 57 (April 1970): 97–109. https://doi.org/10.1093/biomet/57.1.97.
[2] Metropolis, Nicholas, Rosenbluth, Arianna. W., Rosenbluth, Marshall. N., Teller, Augusta. H., and Teller, Edward. "Equation of State Calculations by Fast Computing Machines." The Journal of Chemical Physics 21 (June 1953): 1087–92. https://doi.org/10.1063/1.1699114.
Version History
Introduced in R2022abssm enables you to assume the Student's t distribution for the conditional distribution of the state disturbance or
observation innovations process. These error settings are suited when the process or
measurement errors have excess kurtosis (or is fat-tailed or leptokuric).
Specify the distribution of either error process by using the following name-value
argument when you create a bssm object:
StateDistribution— Distribution of the state disturbance processObservationDistribution— Distribution of the observation innovation process
See Also
Objects
Functions
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
选择网站
选择网站以获取翻译的可用内容,以及查看当地活动和优惠。根据您的位置,我们建议您选择:。
您也可以从以下列表中选择网站:
如何获得最佳网站性能
选择中国网站(中文或英文)以获得最佳网站性能。其他 MathWorks 国家/地区网站并未针对您所在位置的访问进行优化。
美洲
- América Latina (Español)
- Canada (English)
- United States (English)
欧洲
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)