tune

Tune Bayesian state-space model posterior sampler

Since R2022a

Syntax

[params,Proposal] = tune(PriorMdl,Y,params0)

[params,Proposal] = tune(PriorMdl,Y,params0,Name=Value)

Description

The tune function searches for the posterior mode to form proposal distribution moments of the Metropolis-Hastings sampler [1][2]. To improve the proposal distribution, for example, increase the acceptance rate of proposed posterior draws, pass the outputs of tune to simulate.

[params,Proposal] = tune(PriorMdl,Y,params0) returns proposal distribution parameter mean vector params and scale matrix Proposal to improve the Metropolis-Hastings sampler. PriorMdl is the Bayesian state-space model that specifies the state-space model structure (likelihood) and prior distribution, Y is the data for the likelihood, and params0 is the vector of initial values for the unknown state-space model parameters θ in PriorMdl.

example

[params,Proposal] = tune(PriorMdl,Y,params0,Name=Value) specifies additional options using one or more name-value arguments. For example, tune(Mdl,Y,params0,Hessian="opg",Display=false) uses the outer-product of gradients method to compute the Hessian matrix and suppresses the display of the optimized values.

example

Examples

collapse all

Tune Proposal Distribution for Metropolis Sampler of Bayesian State-Space Model

Open Live Script

Simulate observed responses from a known state-space model, then treat the model as Bayesian and draw parameters from the posterior distribution. Tune the proposal distribution of the Metropolis-Hastings sampler by using tune.

Suppose the following state-space model is a data-generating process (DGP).

$[\begin{array}{cccccccccccccccccccc} x_{t, 1} \\ x_{t, 2} \end{array}] = [\begin{array}{cccccccccccccccccccc} 0.5 & 0 \\ 0 & - 0.75 \end{array}] [\begin{array}{cccccccccccccccccccc} x_{t - 1, 1} \\ x_{t - 1, 2} \end{array}] + [\begin{array}{cccccccccccccccccccc} 1 & 0 \\ 0 & 0.5 \end{array}] [\begin{array}{cccccccccccccccccccc} u_{t, 1} \\ u_{t, 2} \end{array}]$

$y_{t} = [\begin{array}{cccccccccccccccccccc} 1 & 1 \end{array}] [\begin{array}{cccccccccccccccccccc} x_{t, 1} \\ x_{t, 2} \end{array}] .$

Create a standard state-space model object ssm that represents the DGP.

trueTheta = [0.5; -0.75; 1; 0.5];
A = [trueTheta(1) 0; 0 trueTheta(2)];
B = [trueTheta(3) 0; 0 trueTheta(4)];
C = [1 1];
DGP = ssm(A,B,C);

Simulate a response path from the DGP.

rng(1); % For reproducibility
y = simulate(DGP,200);

Suppose the structure of the DGP is known, but the state parameters trueTheta are unknown, explicitly

$[\begin{array}{cccccccccccccccccccc} x_{t, 1} \\ x_{t, 2} \end{array}] = [\begin{array}{cccccccccccccccccccc} ϕ_{1} & 0 \\ 0 & ϕ_{2} \end{array}] [\begin{array}{cccccccccccccccccccc} x_{t - 1, 1} \\ x_{t - 1, 2} \end{array}] + [\begin{array}{cccccccccccccccccccc} σ_{1} & 0 \\ 0 & σ_{2} \end{array}] [\begin{array}{cccccccccccccccccccc} u_{t, 1} \\ u_{t, 2} \end{array}]$

$y_{t} = [\begin{array}{cccccccccccccccccccc} 1 & 1 \end{array}] [\begin{array}{cccccccccccccccccccc} x_{t, 1} \\ x_{t, 2} \end{array}] .$

Consider a Bayesian state-space model representing the model with unknown parameters. Arbitrarily assume that the prior distribution of $ϕ_{1}$ , $ϕ_{2}$ , $σ_{1}^{2}$ , and $σ_{2}^{2}$ are independent Gaussian random variables with mean 0.5 and variance 1.

The Local Functions section contains two functions required to specify the Bayesian state-space model. You can use the functions only within this script.

The paramMap function accepts a vector of the unknown state-space model parameters and returns all the following quantities:

A = $[\begin{array}{c} ϕ_{1} & 0 \\ 0 & ϕ_{2} \end{array}]$ .
B = $[\begin{array}{c} σ_{1} & 0 \\ 0 & σ_{2} \end{array}]$ .
C = $[\begin{array}{c} 1 & 1 \end{array}]$ .
D = 0.
Mean0 and Cov0 are empty arrays [], which specify the defaults.
StateType = $[\begin{array}{c} 0 & 0 \end{array}]$ , indicating that each state is stationary.

The paramDistribution function accepts the same vector of unknown parameters as does paramMap, but it returns the log prior density of the parameters at their current values. Specify that parameter values outside the parameter space have log prior density of -Inf.

Create the Bayesian state-space model by passing function handles directly to paramMap and paramDistribution to bssm.

Mdl = bssm(@paramMap,@priorDistribution)

Mdl = 
Mapping that defines a state-space model:
    @paramMap

Log density of parameter prior distribution:
    @priorDistribution

The simulate function requires a proposal distribution scale matrix. You can obtain a data-driven proposal scale matrix by using the tune function. Alternatively, you can supply your own scale matrix.

Obtain a data-driven scale matrix by using the tune function. Supply a random set of initial parameter values.

numParams = 4;
theta0 = rand(numParams,1);
[theta0,Proposal] = tune(Mdl,y,theta0);

Local minimum found.

Optimization completed because the size of the gradient is less than
the value of the optimality tolerance.

         Optimization and Tuning        
      | Params0  Optimized  ProposalStd 
----------------------------------------
 c(1) |  0.6968    0.4459      0.0798   
 c(2) |  0.7662   -0.8781      0.0483   
 c(3) |  0.3425    0.9633      0.0694   
 c(4) |  0.8459    0.3978      0.0726

theta0 is a 4-by-1 estimate of the posterior mode and Proposal is the Hessian matrix. Both outputs are the optimized moments of the proposal distribution, the latter of which is up to a proportionality constant. tune displays convergence information and an estimation table, which you can suppress by using the Display options of the optimizer and tune.

Draw 1000 random parameter vectors from the posterior distribution. Specify the simulated response path as observed responses and the optimized values returned by tune for the initial parameter values and the proposal distribution.

[Theta,accept] = simulate(Mdl,y,theta0,Proposal);
accept

accept = 
0.4010

Theta is a 4-by-1000 matrix of randomly drawn parameters from the posterior distribution. Rows correspond to the elements of the input argument theta of the functions paramMap and priorDistribution.

accept is the proposal acceptance probability. In this case, simulate accepts 40% of the proposal draws.

Local Functions

This example uses the following functions. paramMap is the parameter-to-matrix mapping function and priorDistribution is the log prior distribution of the parameters.

function [A,B,C,D,Mean0,Cov0,StateType] = paramMap(theta)
    A = [theta(1) 0; 0 theta(2)];
    B = [theta(3) 0; 0 theta(4)];
    C = [1 1];
    D = 0;
    Mean0 = [];         % MATLAB uses default initial state mean
    Cov0 = [];          % MATLAB uses initial state covariances
    StateType = [0; 0]; % Two stationary states
end

function logprior = priorDistribution(theta)
    paramconstraints = [(abs(theta(1)) >= 1) (abs(theta(2)) >= 1) ...
        (theta(3) < 0) (theta(4) < 0)];
    if(sum(paramconstraints))
        logprior = -Inf;
    else 
        mu0 = 0.5*ones(numel(theta),1); 
        sigma0 = 1;
        p = normpdf(theta,mu0,sigma0);
        logprior = sum(log(p));
    end
end

Suppress Tuning Displays and Specify Hessian Method

Open Live Script

Consider the following time-varying, state-space model for a DGP:

From periods 1 through 250, the state equation includes stationary AR(2) and MA(1) models, respectively, and the observation model is the weighted sum of the two states.
From periods 251 through 500, the state model includes only the first AR(2) model.
$μ_{0} = [\begin{array}{c} 0.5 & 0.5 & 0 & 0 \end{array}]$ and $Σ_{0}$ is the identity matrix.

Symbolically, the DGP is

$\begin{array}{l} \begin{array}{c} [\begin{array}{cccccccccccccccccccc} x_{1 t} \\ x_{2 t} \\ x_{3 t} \\ x_{4 t} \end{array}] = [\begin{array}{cccccccccccccccccccc} ϕ_{1} & ϕ_{2} & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & θ \\ 0 & 0 & 0 & 0 \end{array}] [\begin{array}{cccccccccccccccccccc} x_{1, t - 1} \\ x_{2, t - 1} \\ x_{3, t - 1} \\ x_{4, t - 1} \end{array}] + [\begin{array}{cccccccccccccccccccc} σ_{1} & 0 \\ 0 & 0 \\ 0 & 1 \\ 0 & 1 \end{array}] [\begin{array}{cccccccccccccccccccc} u_{1 t} \\ u_{2 t} \end{array}] \\ y_{t} = c_{1} (x_{1 t} + x_{3 t}) + σ_{2} ε_{t} . \end{array} f o r t = 1, . . ., 250, \\ \begin{array}{c} [\begin{array}{cccccccccccccccccccc} x_{1 t} \\ x_{2 t} \end{array}] = [\begin{array}{cccccccccccccccccccc} ϕ_{1} & ϕ_{2} & 0 & 0 \\ 1 & 0 & 0 & 0 \end{array}] [\begin{array}{cccccccccccccccccccc} x_{1, t - 1} \\ x_{2, t - 1} \\ x_{3, t - 1} \\ x_{4, t - 1} \end{array}] + [\begin{array}{cccccccccccccccccccc} σ_{1} \\ 0 \end{array}] u_{1 t} \\ y_{t} = c_{2} x_{1 t} + σ_{3} ε_{t} . \end{array} f o r t = 251, \\ \begin{array}{c} [\begin{array}{cccccccccccccccccccc} x_{1 t} \\ x_{2 t} \end{array}] = [\begin{array}{cccccccccccccccccccc} ϕ_{1} & ϕ_{2} \\ 1 & 0 \end{array}] [\begin{array}{cccccccccccccccccccc} x_{1, t - 1} \\ x_{2, t - 1} \end{array}] + [\begin{array}{cccccccccccccccccccc} σ_{1} \\ 0 \end{array}] u_{1 t} \\ y_{t} = c_{2} x_{1 t} + σ_{3} ε_{t} . \end{array} f o r t = 252, . . ., 500 . \end{array}$

where:

The AR(2) parameters ${ϕ_{1}, ϕ_{2}} = {0.5, - 0.2}$ and $σ_{1} = 0.4$ .
The MA(1) parameter $θ = 0.3$ .
The observation equation parameters ${c_{1}, c_{2}} = {2, 3}$ and ${σ_{2}, σ_{3}} = {0.1, 0.2}$ .

Write a function that specifies how the parameters theta and sample size T map to the state-space model matrices, the initial state moments, and the state types. Save this code as a file named timeVariantParamMapBayes.m on your MATLAB® path. Alternatively, open the example to access the function.

type timeVariantParamMapBayes.m

% Copyright 2022 The MathWorks, Inc.

function [A,B,C,D,Mean0,Cov0,StateType] = timeVariantParamMapBayes(theta,T)
% Time-variant, Bayesian state-space model parameter mapping function
% example. This function maps the vector params to the state-space matrices
% (A, B, C, and D), the initial state value and the initial state variance
% (Mean0 and Cov0), and the type of state (StateType). From periods 1
% through T/2, the state model is a stationary AR(2) and an MA(1) model,
% and the observation model is the weighted sum of the two states. From
% periods T/2 + 1 through T, the state model is the AR(2) model only. The
% log prior distribution enforces parameter constraints (see
% flatPriorBSSM.m).
    T1 = floor(T/2);
    T2 = T - T1 - 1;
    A1 = {[theta(1) theta(2) 0 0; 1 0 0 0; 0 0 0 theta(4); 0 0 0 0]};
    B1 = {[theta(3) 0; 0 0; 0 1; 0 1]}; 
    C1 = {theta(5)*[1 0 1 0]};
    D1 = {theta(6)};
    Mean0 = [0.5 0.5 0 0];
    Cov0 = eye(4);
    StateType = [0 0 0 0];
    A2 = {[theta(1) theta(2) 0 0; 1 0 0 0]};
    B2 = {[theta(3); 0]};
    A3 = {[theta(1) theta(2); 1 0]};
    B3 = {[theta(3); 0]}; 
    C3 = {theta(7)*[1 0]};
    D3 = {theta(8)};
    A = [repmat(A1,T1,1); A2; repmat(A3,T2,1)];
    B = [repmat(B1,T1,1); B2; repmat(B3,T2,1)];
    C = [repmat(C1,T1,1); repmat(C3,T2+1,1)];
    D = [repmat(D1,T1,1); repmat(D3,T2+1,1)];
end

Simulate a response path of length 500 from the model.

params = [0.5; -0.2; 0.4; 0.3; 2; 0.1; 3; 0.2];
numObs = 500;
numParams = numel(params);
[A,B,C,D,mean0,Cov0,stateType] = timeVariantParamMapBayes(params,numObs);
DGP = ssm(A,B,C,D,Mean0=mean0,Cov0=Cov0,StateType=stateType);

rng(1)  % For reproducibility
y = simulate(DGP,numObs);
plot(y)
ylabel("y")

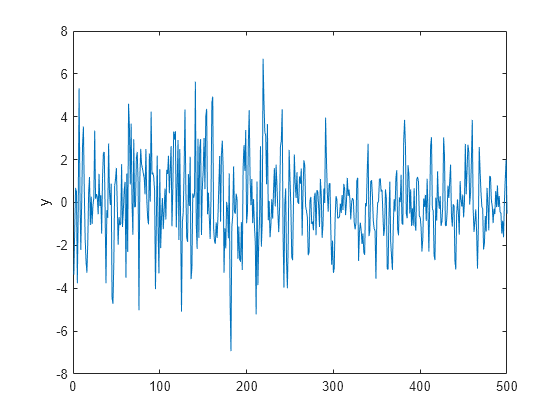
Figure contains an axes object. The axes object with ylabel y contains an object of type line.

Write a function that specifies a flat prior distribution on the state-space model parameters theta. The function returns the scalar log prior for an input set of parameters. Save this code as a file named flatPriorBSSM.m on your MATLAB® path. Alternatively, open the example to access the function.

type flatPriorBSSM.m

% Copyright 2022 The MathWorks, Inc.

function logprior = flatPriorBSSM(theta)
% flatPriorBSSM computes the log of the flat prior density for the eight
% variables in theta (see timeVariantParamMapBayes.m). Log probabilities
% for parameters outside the parameter space are -Inf.

    % theta(1) and theta(2) are lag 1 and lag 2 terms in a stationary AR(2)
    % model. The eigenvalues of the AR(1) representation need to be within
    % the unit circle.
    evalsAR2 = eig([theta(1) theta(2); 1 0]);
    evalsOutUC = sum(abs(evalsAR2) >= 1) > 0;

    % Standard deviations of disturbances and errors (theta(3), theta(6),
    % and theta(8)) need to be positive.
    nonnegsig1 = theta(3) <= 0;
    nonnegsig2 = theta(6) <= 0;
    nonnegsig3 = theta(8) <= 0;

    paramconstraints = [evalsOutUC nonnegsig1 ...
        nonnegsig2 nonnegsig3];
    if sum(paramconstraints) > 0
        logprior = -Inf;
    else
        logprior = 0;   % Prior density is proportional to 1 for all values
                        % in the parameter space.
    end
end

Create a time-varying, Bayesian state-space model that uses the structure of the DGP.

Mdl = bssm(@(params)timeVariantParamMapBayes(params,numObs),@flatPriorBSSM);

Obtain optimized values for the proposal distribution moments by using tune. Initialize the parameter values to a random set of positive values in [0,0.1]. Suppress all tuning displays. Use the Hessian matrix returned by the optimizer of the posterior mode.

params0 = 0.1*rand(numParams,1);
options = optimoptions("fminunc",Display="off");
[params0,Proposal] = tune(Mdl,y,params0,Options=options,Display=false, ...
    Hessian="optimizer");

Draw a sample from the posterior distribution. Supply the optimized parameter estimates. Set the proposal distribution to multivariate $t_{25}$ with a scale matrix proportional. Set the proportionality constant to 0.005.

[PostParams,accept] = simulate(Mdl,y,params0,Proposal, ...
    Dof=25,Proportion=0.1);
accept

accept = 
0.7950

PostParams is an 8-by-1000 matrix of 1000 random draws from the posterior distribution. The Metropolis-Hastings sampler accepted 80% of the proposed draws.

Apply Constraints for Sampler Tuning

Open Live Script

The log joint prior distribution function specifies parameter constraints by attributing a probability of -Inf for arguments outside the support of the distribution. Because posterior sampling does not occur during proposal distribution tuning, it is good practice to additionally specify constraints when you call tune.

Consider a regression of the US unemployment rate onto and real gross national product (rGNP) rate, and suppose the resulting innovations are an ARMA(1,1) process. The state-space form of the relationship is

$\begin{array}{l} [\begin{array}{cccccccccccccccccccc} x_{1, t} \\ x_{2, t} \end{array}] = [\begin{array}{cccccccccccccccccccc} ϕ & θ \\ 0 & 0 \end{array}] [\begin{array}{cccccccccccccccccccc} x_{1, t - 1} \\ x_{2, t - 1} \end{array}] + [\begin{array}{cccccccccccccccccccc} σ \\ 1 \end{array}] u_{t} \\ y_{t} - β Z_{t} = x_{1, t}, \end{array}$

where:

$x_{1, t}$ is the ARMA process.
$x_{2, t}$ is a dummy state for the MA(1) effect.
$y_{t}$ is the observed unemployment rate deflated by a constant and the rGNP rate ( $Z_{t}$ ).
$u_{t}$ is an iid Gaussian series with mean 0 and standard deviation 1.

Load the Nelson-Plosser data set, which contains a table DataTable that has the unemployment rate and rGNP series, among other series.

load Data_NelsonPlosser

Create a variable in DataTable that represents the returns of the raw rGNP series. Because price-to-returns conversion reduces the sample size by one, prepad the series with NaN.

DataTable.RGNPRate = [NaN; price2ret(DataTable.GNPR)];
T = height(DataTable);

Create variables for the regression. Represent the unemployment rate as the observation series and the constant and rGNP rate series as the deflation data $Z_{t}$ .

Z = [ones(T,1) DataTable.RGNPRate];
y = DataTable.UR;

Write a function that specifies how the parameters theta, response series y, and deflation data Z map to the state-space model matrices, the initial state moments, and the state types. Save this code as a file named armaDeflateYBayes.m on your MATLAB® path. Alternatively, open the example to access the function.

type armaDeflateYBayes.m

% Copyright 2022 The MathWorks, Inc.

function [A,B,C,D,Mean0,Cov0,StateType,DeflatedY] = armaDeflateYBayes(theta,y,Z)
% Time-invariant, Bayesian state-space model parameter mapping function
% example. This function maps the vector parameters to the state-space
% matrices (A, B, C, and D), the default initial state value and the
% default initial state variance (Mean0 and Cov0), the type of state
% (StateType), and the deflated observations (DeflatedY). The log prior
% distribution enforces parameter constraints (see flatPriorDeflateY.m).
    A = [theta(1) theta(2); 0 0];
    B = [theta(3); 1]; 
    C = [1 0];
    D = 0;
    Mean0 = [];
    Cov0 = [];
    StateType = [0 0];
    DeflatedY = y - Z*[theta(4); theta(5)];
end

Write a function that specifies a flat prior distribution on the state-space model parameters theta. The function returns the scalar log prior for an input set of parameters. Save this code as a file named flatPriorDeflateY.m on your MATLAB® path. Alternatively, open the example to access the function.

type flatPriorDeflateY.m

% Copyright 2022 The MathWorks, Inc.

function logprior = flatPriorDeflateY(theta)
% flatPriorDeflateY computes the log of the flat prior density for the five
% variables in theta (see armaDeflateYBayes.m). Log probabilities
% for parameters outside the parameter space are -Inf.

    % theta(1) and theta(2) are the AR and MA terms in a stationary
    % ARMA(1,1) model. The AR term must be within the unit circle.
    AROutUC = abs(theta(1)) >= 1;

    % The standard deviation of innovations (theta(3)) must be positive.
    nonnegsig1 = theta(3) <= 0;

    paramconstraints = [AROutUC nonnegsig1];
    if sum(paramconstraints) > 0
        logprior = -Inf;
    else
        logprior = 0;   % Prior density is proportional to 1 for all values
                        % in the parameter space.
    end
end

Create a bssm object representing the Bayesian state-space model. Specify the parameter-to-matrix mapping function as a handle to a function solely of the parameters.

numParams = 5;
Mdl = bssm(@(params)armaDeflateYBayes(params,y,Z),@flatPriorDeflateY)

Mdl = 
Mapping that defines a state-space model:
    @(params)armaDeflateYBayes(params,y,Z)

Log density of parameter prior distribution:
    @flatPriorDeflateY

Tune the proposal distribution. Initialize the Kalman filter with a random set of positive values in [0,0.5]. Suppress the optimization displays. The log prior joint density function flatPriorDeflateY.m specifies that the AR coefficient theta(1) must be within the unit circle and that the observation error standard deviation must be positive theta(3). Specify these constraints for proposal distribution optimization. Use the Hessian matrix returned by fmincon.

rng(1)  % For reproducibility
params0 = 0.5*rand(numParams,1);
options = optimoptions("fmincon",Display="off");    % Constrained optimization requires FMINCON 
lb = -Inf*ones(numParams,1);    % Preallocation
ub = Inf*ones(numParams,1);     % Preallocation
lb([1; 3]) = [-1; 0];
up(1) = 1;
[params0,Proposal] = tune(Mdl,y,params0,Options=options, ...
    Display=false,Hessian="optimizer",Lower=lb,Upper=ub);

Draw a sample from the posterior distribution. Supply the proposal moments returned by tune. Set the proportionality constant to 0.1. Set a burn-in period of 2000 draws, set a thinning factor of 50, and specify retaining 1000 draws.

[PostParams,accept] = simulate(Mdl,y,params0,Proposal,Proportion=0.1, ...
    BurnIn=2000,NumDraws=1000,Thin=50);
accept

accept = 
0.7506

PostParams is a 5-by-1000 matrix of 1000 draws from the posterior distribution. The Metropolis-Hastings sampler accepts 75% of the proposed draws.

paramNames = ["\phi" "\theta" "\sigma" "\beta_0" "\beta_1"];
figure
h = tiledlayout(numParams,1);
for j = 1:numParams
    nexttile
    plot(PostParams(j,:))
    hold on
    ylabel(paramNames(j))
end
title(h,"Posterior Trace Plots")

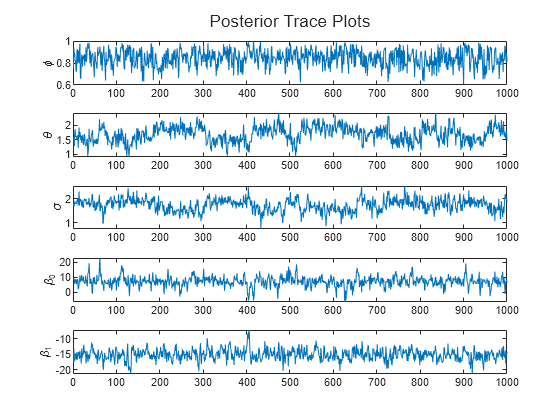
$Figure contains 5 axes objects. Axes object 1 with ylabel \phi contains an object of type line. Axes object 2 with ylabel \theta contains an object of type line. Axes object 3 with ylabel \sigma contains an object of type line. Axes object 4 with ylabel \beta_0 contains an object of type line. Axes object 5 with ylabel \beta_1 contains an object of type line.$

Input Arguments

collapse all

`PriorMdl` — Prior Bayesian state-space model
`bssm` model object

Prior Bayesian state-space model, specified as a bssm model object return by bssm or ssm2bssm.

The function handles of the properties PriorMdl.ParamDistribution and PriorMdl.ParamMap determine the prior and the data likelihood, respectively.

`Y` — Observed response data
numeric matrix | cell vector of numeric vectors

Observed response data, from which tune forms the posterior distribution, specified as a numeric matrix or a cell vector of numeric vectors.

If PriorMdl is time invariant with respect to the observation equation, Y is a T-by-n matrix. Each row of the matrix corresponds to a period and each column corresponds to a particular observation in the model. T is the sample size and n is the number of observations per period. The last row of Y contains the latest observations.
If PriorMdl is time varying with respect to the observation equation, Y is a T-by-1 cell vector. Y{t} contains an n_t-dimensional vector of observations for period t, where t = 1, ..., T. The corresponding dimensions of the coefficient matrices, outputs of PriorMdl.ParamMap, C{t}, and D{t} must be consistent with the matrix in Y{t} for all periods. The last cell of Y contains the latest observations.

NaN elements indicate missing observations. For details on how the Kalman filter accommodates missing observations, see Algorithms.

Data Types: double | cell

`params0` — Initial values for parameters Θ
numeric vector

Initial parameter values for the parameters Θ, specified as a numParams-by-1 numeric vector. Elements of params0 must correspond to the elements of the first input arguments of PriorMdl.ParamMap and PriorMdl.ParamDistribution.

Data Types: double

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: tune(Mdl,Y,params0,Hessian="opg",Display=false) uses the outer-product of gradients method to compute the Hessian matrix and suppresses the display of the optimized values.

Kalman Filter Options

collapse all

`Univariate` — Univariate treatment of multivariate series flag
`false` (default) | `true`

Univariate treatment of a multivariate series flag, specified as a value in this table.

Value	Description
`true`	Applies the univariate treatment of a multivariate series, also known as sequential filtering
`false`	Does not apply sequential filtering

The univariate treatment can accelerate and improve numerical stability of the Kalman filter. However, all observation innovations must be uncorrelated. That is, D_tD_t' must be diagonal, where D_t (t = 1, ..., T) is the output coefficient matrix D of PriorMdl.ParamMap and PriorMdl.ParamDistribution.

Example: Univariate=true

Data Types: logical

`SquareRoot` — Square root filter method flag
`false` (default) | `true`

Square root filter method flag, specified as a value in this table.

Value	Description
`true`	Applies the square root filter method for the Kalman filter
`false`	Does not apply the square root filter method

If you suspect that the eigenvalues of the filtered state or forecasted observation covariance matrices are close to zero, then specify SquareRoot=true. The square root filter is robust to numerical issues arising from the finite precision of calculations, but requires more computational resources.

Example: SquareRoot=true

Data Types: logical

Proposal Tuning Options

collapse all

`Hessian` — Hessian approximation method
`"difference"` (default) | `"diagonal"` | `"opg"` | `"optimizer"` | character vector

Hessian approximation method for the Metropolis-Hastings proposal distribution scale matrix, specified as a value in this table.

Value	Description
`"difference"`	Finite differencing
`"diagonal"`	Diagonalized result of finite differencing
`"opg"`	Outer product of gradients, ignoring the prior distribution
`"optimizer"`	Posterior distribution optimized by `fmincon` or `fminunc`. Specify optimization options by using the `Options` name-value argument.

Tip

The Hessian="difference" setting can be computationally intensive and inaccurate, and the resulting scale matrix can be nonnegative definite. Try one of the other options for better results.

Example: Hessian="opg"

Data Types: char | string

`Lower` — Parameter lower bounds
`[]` (default) | numeric vector

Parameter lower bounds when computing the Hessian matrix (see Hessian), specified as a numParams-by-1 numeric vector.

Lower(j) specifies the lower bound of parameter theta(j), the first input argument of PriorMdl.ParamMap and PriorMdl.ParamDistribution.

The default value [] specifies no lower bounds.

Note

Lower does not apply to posterior simulation. To apply parameter constraints on the posterior, code them in the log prior distribution function PriorMdl.ParamDistribution by setting the log prior of values outside the distribution support to -Inf.

Example: Lower=[0 -5 -1e7]

Data Types: double

`Upper` — Parameter upper bounds
`[]` (default) | numeric vector

Parameter lower bounds when computing the Hessian matrix (see Hessian), specified as a numParams-by-1 numeric vector.

Upper(j) specifies the upper bound of parameter theta(j), the first input argument of PriorMdl.ParamMap and PriorMdl.ParamDistribution.

The default value [] specifies no upper bounds.

Note

Upper does not apply to posterior simulation. To apply parameter constraints on the posterior, code them in the log prior distribution function PriorMdl.ParamDistribution by setting the log prior of values outside the distribution support to -Inf.

Example: Upper=[5 100 1e7]

Data Types: double

`Options` — Optimization options
`optimoptions` optimization controller

Optimization options for the setting Hessian="optimizer", specified as an optimoptions optimization controller. Options replaces default optimization options of the optimizer. For details on altering default values of the optimizer, see the optimization controller optimoptions, the constrained optimization function fmincon, or the unconstrained optimization function fminunc in Optimization Toolbox™.

For example, to change the constraint tolerance to 1e-6, set options = optimoptions(@fmincon,ConstraintTolerance=1e-6,Algorithm="sqp"). Then, pass Options by using Options=options.

By default, tune uses the default options of the optimizer.

`Simplex` — Simplex search flag
`true` (default) | `false`

Simplex search flag to improve initial parameter values, specified as a value in this table.

Value	Description
`true`	Apply simplex search method to improve initial parameter values for proposal optimization. For more details, see fminsearch Algorithm.
`false`	Does not apply simplex search method.

tune applies simplex search when the numerical optimization exit flag is not positive.

Example: Simplex=false

Data Types: logical

`Display` — Proposal tuning results display flag
`true` (default) | `false`

Proposal tuning results display flag, specified as a value in this table.

Value	Description
`true`	Displays tuning results
`false`	Suppresses tuning results display

Example: Display=false

Data Types: logical

Output Arguments

collapse all

`params` — Optimized parameter values
numeric vector

Optimized parameter values for the Metropolis-Hastings sampler, returned as a numParams-by-1 numeric vector. params(j) contains the optimized value of parameter theta(j), where theta is the first input argument of PriorMdl.ParamMap and PriorMdl.ParamDistribution.

When you call simulate, pass params as the initial parameter values input params0.

`Proposal` — Proposal distribution covariance/scale matrix
numeric matrix

Proposal distribution covariance/scale matrix for the Metropolis-Hastings sampler, specified as a numParams-by-numParams numeric matrix. Rows and columns of Proposal correspond to elements in params.

Proposal is the scale matrix up to a proportionality constant, which is specified by the Proportion name-value argument of estimate and simulate.

The proposal distribution is multivariate normal or Student's t.

When you call simulate, pass Proposal as the proposal distribution scale matrix input Proposal.

Data Types: double

Algorithms

The Metropolis-Hastings sampler requires a carefully specified proposal distribution. Under the assumption of a Gaussian linear state-space model, tune tunes the sampler by performing numerical optimization to search for the posterior mode. A reasonable proposal for the multivariate normal or t distribution is the inverse of the negative Hessian matrix, which tune evaluates at the resulting posterior mode.
When tune tunes the proposal distribution, the optimizer that tune uses to search for the posterior mode before computing the Hessian matrix depends on your specifications.
- tune uses fminunc by default.
- tune uses fmincon when you perform constrained optimization by specifying the Lower or Upper name-value argument.
- tune further refines the solution returned by fminunc or fmincon by using fminsearch when Simplex=true, which is the default.

References

[1] Hastings, Wilfred K. "Monte Carlo Sampling Methods Using Markov Chains and Their Applications." Biometrika 57 (April 1970): 97–109. https://doi.org/10.1093/biomet/57.1.97.

[2] Metropolis, Nicholas, Rosenbluth, Arianna. W., Rosenbluth, Marshall. N., Teller, Augusta. H., and Teller, Edward. "Equation of State Calculations by Fast Computing Machines." The Journal of Chemical Physics 21 (June 1953): 1087–92. https://doi.org/10.1063/1.1699114.

Version History

Introduced in R2022a

tune

Syntax

Description

Examples

Tune Proposal Distribution for Metropolis Sampler of Bayesian State-Space Model

Suppress Tuning Displays and Specify Hessian Method

Apply Constraints for Sampler Tuning

Input Arguments

`PriorMdl` — Prior Bayesian state-space model
`bssm` model object

`Y` — Observed response data
numeric matrix | cell vector of numeric vectors

`params0` — Initial values for parameters Θ
numeric vector

Name-Value Arguments

`Univariate` — Univariate treatment of multivariate series flag
`false` (default) | `true`

`SquareRoot` — Square root filter method flag
`false` (default) | `true`

`Hessian` — Hessian approximation method
`"difference"` (default) | `"diagonal"` | `"opg"` | `"optimizer"` | character vector

`Lower` — Parameter lower bounds
`[]` (default) | numeric vector

`Upper` — Parameter upper bounds
`[]` (default) | numeric vector

`Options` — Optimization options
`optimoptions` optimization controller

`Simplex` — Simplex search flag
`true` (default) | `false`

`Display` — Proposal tuning results display flag
`true` (default) | `false`

Output Arguments

`params` — Optimized parameter values
numeric vector

`Proposal` — Proposal distribution covariance/scale matrix
numeric matrix

Algorithms

References

Version History

See Also

Objects

Functions

Topics

tune

Syntax

Description

Examples

Tune Proposal Distribution for Metropolis Sampler of Bayesian State-Space Model

Suppress Tuning Displays and Specify Hessian Method

Apply Constraints for Sampler Tuning

Input Arguments

PriorMdl — Prior Bayesian state-space model bssm model object

Y — Observed response data numeric matrix | cell vector of numeric vectors

params0 — Initial values for parameters Θ numeric vector

Name-Value Arguments

Univariate — Univariate treatment of multivariate series flag false (default) | true

SquareRoot — Square root filter method flag false (default) | true

Hessian — Hessian approximation method "difference" (default) | "diagonal" | "opg" | "optimizer" | character vector

Lower — Parameter lower bounds [] (default) | numeric vector

Upper — Parameter upper bounds [] (default) | numeric vector

Options — Optimization options optimoptions optimization controller

Simplex — Simplex search flag true (default) | false

Display — Proposal tuning results display flag true (default) | false

Output Arguments

params — Optimized parameter values numeric vector

Proposal — Proposal distribution covariance/scale matrix numeric matrix

Algorithms

References

Version History

See Also

Objects

Functions

Topics

`PriorMdl` — Prior Bayesian state-space model
`bssm` model object

`Y` — Observed response data
numeric matrix | cell vector of numeric vectors

`params0` — Initial values for parameters Θ
numeric vector

`Univariate` — Univariate treatment of multivariate series flag
`false` (default) | `true`

`SquareRoot` — Square root filter method flag
`false` (default) | `true`

`Hessian` — Hessian approximation method
`"difference"` (default) | `"diagonal"` | `"opg"` | `"optimizer"` | character vector

`Lower` — Parameter lower bounds
`[]` (default) | numeric vector

`Upper` — Parameter upper bounds
`[]` (default) | numeric vector

`Options` — Optimization options
`optimoptions` optimization controller

`Simplex` — Simplex search flag
`true` (default) | `false`

`Display` — Proposal tuning results display flag
`true` (default) | `false`

`params` — Optimized parameter values
numeric vector

`Proposal` — Proposal distribution covariance/scale matrix
numeric matrix