simulate

Simulate posterior draws of Bayesian state-space model parameters

Since R2022a

Syntax

[Params,accept] = simulate(PriorMdl,Y,params0,Proposal)

[Params,accept] = simulate(PriorMdl,Y,params0,Proposal,Name=Value)

[Params,accept,Output] = simulate(PriorMdl,Y,params0,Proposal,Name=Value)

Description

[Params,accept] = simulate(PriorMdl,Y,params0,Proposal) returns 1000 random vectors of state-space model parameters Params drawn from the posterior distribution Π(θ|Y), where PriorMdl specifies the prior distribution and data likelihood, and Y is the observed response data. params0 is the set of initial parameter values and Proposal is the covariance matrix of the proposal distribution of the Metropolis-Hastings (MH) sampler [1][2]. accept is the acceptance rate of the proposal draws.

example

[Params,accept] = simulate(PriorMdl,Y,params0,Proposal,Name=Value) specifies options using one or more name-value arguments. For example, simulate(PriorMdl,Y,params0,Proposal,NumDraws=1e6,Thin=3,DoF=10) uses the multivariate t₁₀ distribution for the Metropolis-Hastings proposal, draws 3e6 random vectors of parameters, and thins the sample to reduce serial correlation by discarding every 2 draws until it retains 1e6 draws.

example

[Params,accept,Output] = simulate(PriorMdl,Y,params0,Proposal,Name=Value) also returns the output Output of the custom function that monitors the Markov-chain Monte Carlo (MCMC) algorithm at each iteration, specified by the OutputFunction name-value argument.

example

Examples

collapse all

Draw Random Parameters from Posterior Distribution of Time-Invariant Model

Open Live Script

Simulate observed responses from a known state-space model, then treat the model as Bayesian and draw parameters from the posterior distribution.

Suppose the following state-space model is a data-generating process (DGP).

$[\begin{array}{cccccccccccccccccccc} x_{t, 1} \\ x_{t, 2} \end{array}] = [\begin{array}{cccccccccccccccccccc} 0.5 & 0 \\ 0 & - 0.75 \end{array}] [\begin{array}{cccccccccccccccccccc} x_{t - 1, 1} \\ x_{t - 1, 2} \end{array}] + [\begin{array}{cccccccccccccccccccc} 1 & 0 \\ 0 & 0.5 \end{array}] [\begin{array}{cccccccccccccccccccc} u_{t, 1} \\ u_{t, 2} \end{array}]$

$y_{t} = [\begin{array}{cccccccccccccccccccc} 1 & 1 \end{array}] [\begin{array}{cccccccccccccccccccc} x_{t, 1} \\ x_{t, 2} \end{array}] .$

Create a standard state-space model object ssm that represents the DGP.

trueTheta = [0.5; -0.75; 1; 0.5];
A = [trueTheta(1) 0; 0 trueTheta(2)];
B = [trueTheta(3) 0; 0 trueTheta(4)];
C = [1 1];
DGP = ssm(A,B,C);

Simulate a response path from the DGP.

rng(1); % For reproducibility
y = simulate(DGP,200);

Suppose the structure of the DGP is known, but the state parameters trueTheta are unknown, explicitly

$[\begin{array}{cccccccccccccccccccc} x_{t, 1} \\ x_{t, 2} \end{array}] = [\begin{array}{cccccccccccccccccccc} ϕ_{1} & 0 \\ 0 & ϕ_{2} \end{array}] [\begin{array}{cccccccccccccccccccc} x_{t - 1, 1} \\ x_{t - 1, 2} \end{array}] + [\begin{array}{cccccccccccccccccccc} σ_{1} & 0 \\ 0 & σ_{2} \end{array}] [\begin{array}{cccccccccccccccccccc} u_{t, 1} \\ u_{t, 2} \end{array}]$

$y_{t} = [\begin{array}{cccccccccccccccccccc} 1 & 1 \end{array}] [\begin{array}{cccccccccccccccccccc} x_{t, 1} \\ x_{t, 2} \end{array}] .$

Consider a Bayesian state-space model representing the model with unknown parameters. Arbitrarily assume that the prior distribution of $ϕ_{1}$ , $ϕ_{2}$ , $σ_{1}^{2}$ , and $σ_{2}^{2}$ are independent Gaussian random variables with mean 0.5 and variance 1.

The Local Functions section contains two functions required to specify the Bayesian state-space model. You can use the functions only within this script.

The paramMap function accepts a vector of the unknown state-space model parameters and returns all the following quantities:

A = $[\begin{array}{c} ϕ_{1} & 0 \\ 0 & ϕ_{2} \end{array}]$ .
B = $[\begin{array}{c} σ_{1} & 0 \\ 0 & σ_{2} \end{array}]$ .
C = $[\begin{array}{c} 1 & 1 \end{array}]$ .
D = 0.
Mean0 and Cov0 are empty arrays [], which specify the defaults.
StateType = $[\begin{array}{c} 0 & 0 \end{array}]$ , indicating that each state is stationary.

The paramDistribution function accepts the same vector of unknown parameters as does paramMap, but it returns the log prior density of the parameters at their current values. Specify that parameter values outside the parameter space have log prior density of -Inf.

Create the Bayesian state-space model by passing function handles directly to paramMap and paramDistribution to bssm.

Mdl = bssm(@paramMap,@priorDistribution)

Mdl = 
Mapping that defines a state-space model:
    @paramMap

Log density of parameter prior distribution:
    @priorDistribution

The simulate function requires a proposal distribution scale matrix. You can obtain a data-driven proposal scale matrix by using the tune function. Alternatively, you can supply your own scale matrix.

Obtain a data-driven scale matrix by using the tune function. Supply a random set of initial parameter values, and shut off the estimation summary display.

numParams = 4;
theta0 = rand(numParams,1);
[theta0,Proposal] = tune(Mdl,y,theta0,Display=false);

Local minimum found.

Optimization completed because the size of the gradient is less than
the value of the optimality tolerance.

Draw 1000 random parameter vectors from the posterior distribution. Specify the simulated response path as observed responses and the optimized values returned by tune for the initial parameter values and the proposal distribution.

[Theta,accept] = simulate(Mdl,y,theta0,Proposal);
accept

accept = 
0.4010

Theta is a 4-by-1000 matrix of randomly drawn parameters from the posterior distribution. Rows correspond to the elements of the input argument theta of the functions paramMap and priorDistribution.

accept is the proposal acceptance probability. In this case, simulate accepts 40% of the proposal draws.

Create trace plots of the parameters.

paramNames = ["\phi_1" "\phi_2" "\sigma_1" "\sigma_2"];
figure
h = tiledlayout(4,1);
for j = 1:numParams
    nexttile
    plot(Theta(j,:))
    hold on
    yline(trueTheta(j))
    ylabel(paramNames(j))
end
title(h,"Posterior Trace Plots")

$Figure contains 4 axes objects. Axes object 1 with ylabel \phi_1 contains 2 objects of type line, constantline. Axes object 2 with ylabel \phi_2 contains 2 objects of type line, constantline. Axes object 3 with ylabel \sigma_1 contains 2 objects of type line, constantline. Axes object 4 with ylabel \sigma_2 contains 2 objects of type line, constantline.$

The sampler eventually settles at near the true values of the parameters. In this case, the sample shows serial correlation and transient behavior. You can remedy serial correlation in the sample by adjusting the Thin name-value argument, and you can remedy transient effects by increasing the burn-in period using the BurnIn name-value argument.

Local Functions

This example uses the following functions. paramMap is the parameter-to-matrix mapping function and priorDistribution is the log prior distribution of the parameters.

function [A,B,C,D,Mean0,Cov0,StateType] = paramMap(theta)
    A = [theta(1) 0; 0 theta(2)];
    B = [theta(3) 0; 0 theta(4)];
    C = [1 1];
    D = 0;
    Mean0 = [];         % MATLAB uses default initial state mean
    Cov0 = [];          % MATLAB uses initial state covariances
    StateType = [0; 0]; % Two stationary states
end

function logprior = priorDistribution(theta)
    paramconstraints = [(abs(theta(1)) >= 1) (abs(theta(2)) >= 1) ...
        (theta(3) < 0) (theta(4) < 0)];
    if(sum(paramconstraints))
        logprior = -Inf;
    else 
        mu0 = 0.5*ones(numel(theta),1); 
        sigma0 = 1;
        p = normpdf(theta,mu0,sigma0);
        logprior = sum(log(p));
    end
end

Improve Markov Chain Convergence

Open Live Script

Consider the model in the example Draw Random Parameters from Posterior Distribution of Time-Invariant Model. Improve the Markov chain convergence by adjusting sampler options.

Create a standard state-space model object ssm that represents the DGP, and then simulate a response path.

trueTheta = [0.5; -0.75; 1; 0.5];
A = [trueTheta(1) 0; 0 trueTheta(2)];
B = [trueTheta(3) 0; 0 trueTheta(4)];
C = [1 1];
DGP = ssm(A,B,C);

rng(1); % For reproducibility
y = simulate(DGP,200);

Create the Bayesian state-space model by passing function handles directly to paramMap and paramDistribution to bssm (the functions are in Local Functions).

Mdl = bssm(@paramMap,@priorDistribution)

Mdl = 
Mapping that defines a state-space model:
    @paramMap

Log density of parameter prior distribution:
    @priorDistribution

Simulate random parameter vectors from the posterior distribution. Specify the simulated response path as observed responses, and obtain an optimal proposal distribution by using tune and shut off all optimization displays. The plots in Draw Random Parameters from Posterior Distribution of Time-Invariant Model suggest that the Markov chain settles after 500 draws. Therefore, specify a burn-in period of 500 (BurnIn=500). Specify thinning the sample by keeping the first draw of each set of 30 successive draws (Thin=30). Retain 2000 random parameter vectors (NumDraws=2000).

numParams = 4;
theta0 = rand(numParams,1);
options = optimoptions("fminunc",Display="off");
[theta0,Proposal] = tune(Mdl,y,theta0,Display=false,Options=options);

[Theta,accept] = simulate(Mdl,y,theta0,Proposal, ...
    NumDraws=2000,BurnIn=500,Thin=30);
accept

accept = 
0.3885

Theta is a 4-by-2000 matrix of randomly drawn parameters from the posterior distribution. Rows correspond to the elements of the input argument theta of the functions paramMap and priorDistribution.

accept is the proposal acceptance probability. In this case, simulate accepts 39% of the proposal draws.

Create trace plots and correlograms of the parameters.

paramNames = ["\phi_1" "\phi_2" "\sigma_1" "\sigma_2"];
figure
h = tiledlayout(4,1);
for j = 1:numParams
    nexttile
    plot(Theta(j,:))
    hold on
    yline(trueTheta(j))
    ylabel(paramNames(j))
end
title(h,"Posterior Trace Plots")

figure
h = tiledlayout(4,1);
for j = 1:numParams
    nexttile
    autocorr(Theta(j,:));
    ylabel(paramNames(j));
    title([]);
end
title(h,"Posterior Sample Correlograms")

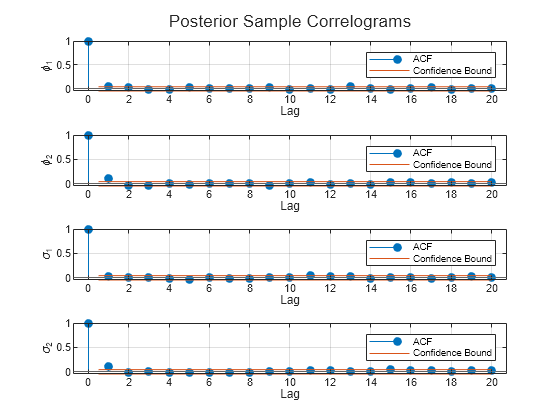
$Figure contains 4 axes objects. Axes object 1 with xlabel Lag, ylabel \phi_1 contains 4 objects of type stem, line, constantline. These objects represent ACF, Confidence Bound. Axes object 2 with xlabel Lag, ylabel \phi_2 contains 4 objects of type stem, line, constantline. These objects represent ACF, Confidence Bound. Axes object 3 with xlabel Lag, ylabel \sigma_1 contains 4 objects of type stem, line, constantline. These objects represent ACF, Confidence Bound. Axes object 4 with xlabel Lag, ylabel \sigma_2 contains 4 objects of type stem, line, constantline. These objects represent ACF, Confidence Bound.$

The sampler quickly settles near the true values of the parameters. The sample shows little serial correlation and no transient behavior.

Local Functions

This example uses the following functions. paramMap is the parameter-to-matrix mapping function and priorDistribution is the log prior distribution of the parameters.

function [A,B,C,D,Mean0,Cov0,StateType] = paramMap(theta)
    A = [theta(1) 0; 0 theta(2)];
    B = [theta(3) 0; 0 theta(4)];
    C = [1 1];
    D = 0;
    Mean0 = [];         % MATLAB uses default initial state mean
    Cov0 = [];          % MATLAB uses initial state covariances
    StateType = [0; 0]; % Two stationary states
end

function logprior = priorDistribution(theta)
    paramconstraints = [(abs(theta(1)) >= 1) (abs(theta(2)) >= 1) ...
        (theta(3) < 0) (theta(4) < 0)];
    if(sum(paramconstraints))
        logprior = -Inf;
    else 
        mu0 = 0.5*ones(numel(theta),1); 
        sigma0 = 1;
        p = normpdf(theta,mu0,sigma0);
        logprior = sum(log(p));
    end
end

Simulate Parameters from Posterior of Time-Varying Model

Open Live Script

Consider the following time-varying, state-space model for a DGP:

From periods 1 through 250, the state equation includes stationary AR(2) and MA(1) models, respectively, and the observation model is the weighted sum of the two states.
From periods 251 through 500, the state model includes only the first AR(2) model.
$μ_{0} = [\begin{array}{c} 0.5 & 0.5 & 0 & 0 \end{array}]$ and $Σ_{0}$ is the identity matrix.

Symbolically, the DGP is

$\begin{array}{l} \begin{array}{c} [\begin{array}{cccccccccccccccccccc} x_{1 t} \\ x_{2 t} \\ x_{3 t} \\ x_{4 t} \end{array}] = [\begin{array}{cccccccccccccccccccc} ϕ_{1} & ϕ_{2} & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & θ \\ 0 & 0 & 0 & 0 \end{array}] [\begin{array}{cccccccccccccccccccc} x_{1, t - 1} \\ x_{2, t - 1} \\ x_{3, t - 1} \\ x_{4, t - 1} \end{array}] + [\begin{array}{cccccccccccccccccccc} σ_{1} & 0 \\ 0 & 0 \\ 0 & 1 \\ 0 & 1 \end{array}] [\begin{array}{cccccccccccccccccccc} u_{1 t} \\ u_{2 t} \end{array}] \\ y_{t} = c_{1} (x_{1 t} + x_{3 t}) + σ_{2} ε_{t} . \end{array} f o r t = 1, . . ., 250, \\ \begin{array}{c} [\begin{array}{cccccccccccccccccccc} x_{1 t} \\ x_{2 t} \end{array}] = [\begin{array}{cccccccccccccccccccc} ϕ_{1} & ϕ_{2} & 0 & 0 \\ 1 & 0 & 0 & 0 \end{array}] [\begin{array}{cccccccccccccccccccc} x_{1, t - 1} \\ x_{2, t - 1} \\ x_{3, t - 1} \\ x_{4, t - 1} \end{array}] + [\begin{array}{cccccccccccccccccccc} σ_{1} \\ 0 \end{array}] u_{1 t} \\ y_{t} = c_{2} x_{1 t} + σ_{3} ε_{t} . \end{array} f o r t = 251, \\ \begin{array}{c} [\begin{array}{cccccccccccccccccccc} x_{1 t} \\ x_{2 t} \end{array}] = [\begin{array}{cccccccccccccccccccc} ϕ_{1} & ϕ_{2} \\ 1 & 0 \end{array}] [\begin{array}{cccccccccccccccccccc} x_{1, t - 1} \\ x_{2, t - 1} \end{array}] + [\begin{array}{cccccccccccccccccccc} σ_{1} \\ 0 \end{array}] u_{1 t} \\ y_{t} = c_{2} x_{1 t} + σ_{3} ε_{t} . \end{array} f o r t = 252, . . ., 500 . \end{array}$

where:

The AR(2) parameters ${ϕ_{1}, ϕ_{2}} = {0.5, - 0.2}$ and $σ_{1} = 0.4$ .
The MA(1) parameter $θ = 0.3$ .
The observation equation parameters ${c_{1}, c_{2}} = {2, 3}$ and ${σ_{2}, σ_{3}} = {0.1, 0.2}$ .

Write a function that specifies how the parameters theta and sample size T map to the state-space model matrices, the initial state moments, and the state types. Save this code as a file named timeVariantParamMapBayes.m on your MATLAB® path. Alternatively, open the example to access the function.

type timeVariantParamMapBayes.m

% Copyright 2022 The MathWorks, Inc.

function [A,B,C,D,Mean0,Cov0,StateType] = timeVariantParamMapBayes(theta,T)
% Time-variant, Bayesian state-space model parameter mapping function
% example. This function maps the vector params to the state-space matrices
% (A, B, C, and D), the initial state value and the initial state variance
% (Mean0 and Cov0), and the type of state (StateType). From periods 1
% through T/2, the state model is a stationary AR(2) and an MA(1) model,
% and the observation model is the weighted sum of the two states. From
% periods T/2 + 1 through T, the state model is the AR(2) model only. The
% log prior distribution enforces parameter constraints (see
% flatPriorBSSM.m).
    T1 = floor(T/2);
    T2 = T - T1 - 1;
    A1 = {[theta(1) theta(2) 0 0; 1 0 0 0; 0 0 0 theta(4); 0 0 0 0]};
    B1 = {[theta(3) 0; 0 0; 0 1; 0 1]}; 
    C1 = {theta(5)*[1 0 1 0]};
    D1 = {theta(6)};
    Mean0 = [0.5 0.5 0 0];
    Cov0 = eye(4);
    StateType = [0 0 0 0];
    A2 = {[theta(1) theta(2) 0 0; 1 0 0 0]};
    B2 = {[theta(3); 0]};
    A3 = {[theta(1) theta(2); 1 0]};
    B3 = {[theta(3); 0]}; 
    C3 = {theta(7)*[1 0]};
    D3 = {theta(8)};
    A = [repmat(A1,T1,1); A2; repmat(A3,T2,1)];
    B = [repmat(B1,T1,1); B2; repmat(B3,T2,1)];
    C = [repmat(C1,T1,1); repmat(C3,T2+1,1)];
    D = [repmat(D1,T1,1); repmat(D3,T2+1,1)];
end

Simulate a response path of length 500 from the model.

params = [0.5; -0.2; 0.4; 0.3; 2; 0.1; 3; 0.2];
numObs = 500;
numParams = numel(params);
[A,B,C,D,mean0,Cov0,stateType] = timeVariantParamMapBayes(params,numObs);
DGP = ssm(A,B,C,D,Mean0=mean0,Cov0=Cov0,StateType=stateType);

rng(1)  % For reproducibility
y = simulate(DGP,numObs);
plot(y)
ylabel("y")

Figure contains an axes object. The axes object with ylabel y contains an object of type line.

Write a function that specifies a flat prior distribution on the state-space model parameters theta. The function returns the scalar log prior for an input set of parameters. Save this code as a file named flatPriorBSSM.m on your MATLAB® path. Alternatively, open the example to access the function.

type flatPriorBSSM.m

% Copyright 2022 The MathWorks, Inc.

function logprior = flatPriorBSSM(theta)
% flatPriorBSSM computes the log of the flat prior density for the eight
% variables in theta (see timeVariantParamMapBayes.m). Log probabilities
% for parameters outside the parameter space are -Inf.

    % theta(1) and theta(2) are lag 1 and lag 2 terms in a stationary AR(2)
    % model. The eigenvalues of the AR(1) representation need to be within
    % the unit circle.
    evalsAR2 = eig([theta(1) theta(2); 1 0]);
    evalsOutUC = sum(abs(evalsAR2) >= 1) > 0;

    % Standard deviations of disturbances and errors (theta(3), theta(6),
    % and theta(8)) need to be positive.
    nonnegsig1 = theta(3) <= 0;
    nonnegsig2 = theta(6) <= 0;
    nonnegsig3 = theta(8) <= 0;

    paramconstraints = [evalsOutUC nonnegsig1 ...
        nonnegsig2 nonnegsig3];
    if sum(paramconstraints) > 0
        logprior = -Inf;
    else
        logprior = 0;   % Prior density is proportional to 1 for all values
                        % in the parameter space.
    end
end

Create a time-varying, Bayesian state-space model that uses the structure of the DGP.

Mdl = bssm(@(params)timeVariantParamMapBayes(params,numObs),@flatPriorBSSM);

Draw a sample from the posterior distribution. Initialize the parameter values to a random set of positive values in [0,0.5]. Set the proposal distribution to multivariate $t_{25}$ with a scale matrix proportional. Set the proportionality constant to 0.005.

params0 = 0.5*rand(numParams,1);
options = optimoptions("fminunc",Display="off");
[params0,Proposal] = tune(Mdl,y,params0,Options=options,Display=false);
[PostParams,accept] = simulate(Mdl,y,params0,Proposal, ...
    DoF=25,Proportion=0.005);
accept

accept = 
0.7460

PostParams is an 8-by-1000 matrix of 1000 random draws from the posterior distribution. The Metropolis-Hastings sampler accepted 75% of the proposed draws.

Draw Posterior Sample From Model with Deflated Response

Open Live Script

When you work with a state-space model that contains a deflated response variable, you must have data for the predictors.

Consider a regression of the US unemployment rate onto and real gross national product (rGNP) rate, and suppose the resulting innovations are an ARMA(1,1) process. The state-space form of the relationship is

$\begin{array}{l} [\begin{array}{cccccccccccccccccccc} x_{1, t} \\ x_{2, t} \end{array}] = [\begin{array}{cccccccccccccccccccc} ϕ & θ \\ 0 & 0 \end{array}] [\begin{array}{cccccccccccccccccccc} x_{1, t - 1} \\ x_{2, t - 1} \end{array}] + [\begin{array}{cccccccccccccccccccc} σ \\ 1 \end{array}] u_{t} \\ y_{t} - β Z_{t} = x_{1, t}, \end{array}$

where:

$x_{1, t}$ is the ARMA process.
$x_{2, t}$ is a dummy state for the MA(1) effect.
$y_{t}$ is the observed unemployment rate deflated by a constant and the rGNP rate ( $Z_{t}$ ).
$u_{t}$ is an iid Gaussian series with mean 0 and standard deviation 1.

Load the Nelson-Plosser data set, which contains a table DataTable that has the unemployment rate and rGNP series, among other series.

load Data_NelsonPlosser

Create a variable in DataTable that represents the returns of the raw rGNP series. Because price-to-returns conversion reduces the sample size by one, prepad the series with NaN.

DataTable.RGNPRate = [NaN; price2ret(DataTable.GNPR)];
T = height(DataTable);

Create variables for the regression. Represent the unemployment rate as the observation series and the constant and rGNP rate series as the deflation data $Z_{t}$ .

Z = [ones(T,1) DataTable.RGNPRate];
y = DataTable.UR;

Write a function that specifies how the parameters theta, response series y, and deflation data Z map to the state-space model matrices, the initial state moments, and the state types. Save this code as a file named armaDeflateYBayes.m on your MATLAB® path. Alternatively, open the example to access the function.

type armaDeflateYBayes.m

% Copyright 2022 The MathWorks, Inc.

function [A,B,C,D,Mean0,Cov0,StateType,DeflatedY] = armaDeflateYBayes(theta,y,Z)
% Time-invariant, Bayesian state-space model parameter mapping function
% example. This function maps the vector parameters to the state-space
% matrices (A, B, C, and D), the default initial state value and the
% default initial state variance (Mean0 and Cov0), the type of state
% (StateType), and the deflated observations (DeflatedY). The log prior
% distribution enforces parameter constraints (see flatPriorDeflateY.m).
    A = [theta(1) theta(2); 0 0];
    B = [theta(3); 1]; 
    C = [1 0];
    D = 0;
    Mean0 = [];
    Cov0 = [];
    StateType = [0 0];
    DeflatedY = y - Z*[theta(4); theta(5)];
end

Write a function that specifies a flat prior distribution on the state-space model parameters theta. The function returns the scalar log prior for an input set of parameters. Save this code as a file named flatPriorDeflateY.m on your MATLAB® path. Alternatively, open the example to access the function.

type flatPriorDeflateY.m

% Copyright 2022 The MathWorks, Inc.

function logprior = flatPriorDeflateY(theta)
% flatPriorDeflateY computes the log of the flat prior density for the five
% variables in theta (see armaDeflateYBayes.m). Log probabilities
% for parameters outside the parameter space are -Inf.

    % theta(1) and theta(2) are the AR and MA terms in a stationary
    % ARMA(1,1) model. The AR term must be within the unit circle.
    AROutUC = abs(theta(1)) >= 1;

    % The standard deviation of innovations (theta(3)) must be positive.
    nonnegsig1 = theta(3) <= 0;

    paramconstraints = [AROutUC nonnegsig1];
    if sum(paramconstraints) > 0
        logprior = -Inf;
    else
        logprior = 0;   % Prior density is proportional to 1 for all values
                        % in the parameter space.
    end
end

Create a bssm object representing the Bayesian state-space model. Specify the parameter-to-matrix mapping function as a handle to a function solely of the parameters.

numParams = 5;
Mdl = bssm(@(params)armaDeflateYBayes(params,y,Z),@flatPriorDeflateY)

Mdl = 
Mapping that defines a state-space model:
    @(params)armaDeflateYBayes(params,y,Z)

Log density of parameter prior distribution:
    @flatPriorDeflateY

Draw a sample from the posterior distribution. Initialize the MCMC algorithm with a random set of positive values in [0,0.5]. Obtain an optimal set of proposal distribution moments for the sampler by using tune. Set the proportionality constant to 0.01. Set a burn-in period of 2000 draws, set a thinning factor of 50, and specify retaining 1000 draws.

rng(1)  % For reproducibility
params0 = 0.5*rand(numParams,1);
options = optimoptions("fminunc",Display="off");
[params0,Proposal] = tune(Mdl,y,params0,Options=options, ...
    Display=false);
[PostParams,accept] = simulate(Mdl,y,params0,Proposal,Proportion=0.01, ...
    BurnIn=2000,NumDraws=1000,Thin=50);
accept

accept = 
0.9200

PostParams is a 5-by-1000 matrix of 1000 draws from the posterior distribution. The Metropolis-Hastings sampler accepts 92% of the proposed draws.

paramNames = ["\phi" "\theta" "\sigma" "\beta_0" "\beta_1"];
figure
h = tiledlayout(numParams,1);
for j = 1:numParams
    nexttile
    plot(PostParams(j,:))
    hold on
    ylabel(paramNames(j))
end
title(h,"Posterior Trace Plots")

$Figure contains 5 axes objects. Axes object 1 with ylabel \phi contains an object of type line. Axes object 2 with ylabel \theta contains an object of type line. Axes object 3 with ylabel \sigma contains an object of type line. Axes object 4 with ylabel \beta_0 contains an object of type line. Axes object 5 with ylabel \beta_1 contains an object of type line.$

All samples appear to suffer from autocorrelation. To improve the Markov chain, experiment with the Thin option.

Access Degrees of Freedom Posterior Draws Using Output Function

Open Live Script

The estimate and simulate functions do not return posterior draws of the degrees of freedom parameters of multivariate t-distributed state disturbances and observation innovations. However, you can write an output function that stores the degrees of freedom draws at each iteration of the MCMC algorithm, and pass it to simulate to obtain the draws.

Consider the following DGP.

$y_{t} = [\begin{array}{cccccccccccccccccccc} 1 & 3 \end{array}] [\begin{array}{cccccccccccccccccccc} x_{t, 1} \\ x_{t, 2} \end{array}] .$

The true value of the state-space parameter set $Θ = {ϕ_{1}, ϕ_{2}, σ_{1}, σ_{2}} = {0.5, - 0.75, 1, 0.5}$ .
The state disturbances $u_{1, t}$ and $u_{2, t}$ are jointly a multivariate Student's $t$ random series with $ν_{u} = 5$ degrees of freedom.

Create a vector autoregression (VAR) model that represents the state equation of the DGP.

trueTheta = [0.5; -0.75; 1; 0.5];
trueDoF = 5;
phi = [trueTheta(1) 0; 0 trueTheta(2)];
Sigma = [trueTheta(3)^2 0; 0 trueTheta(4)^2];
DGP = varm(AR={phi},Covariance=Sigma,Constant=[0; 0]);

Filter a random 2-D multivariate central $t$ series of length 500 through the VAR model to obtain state values. Set the degrees of freedom to 5.

rng(10)  % For reproducibility
T = 500;
trueU = mvtrnd(eye(DGP.NumSeries),trueDoF,T);
X = filter(DGP,trueU);

Obtain a series of observations from the DGP by the linear combination $y_{t} = x_{1, e} + 3 x_{2, t}$ .

C = [1 3];
y = X*C';

Consider a Bayesian state-space model representing the model with parameters $Θ$ and $ν_{u}$ treated as unknown. Arbitrarily assume that the prior distribution of the parameters in $Θ$ are independent Gaussian random variables with mean 0.5 and variance 1. Assume that the prior on the degrees of freedom $ν_{u}$ is flat. The functions in Local Functions specify the state-space structure and prior distributions.

Create the Bayesian state-space model by passing function handles to the paramMap and priorDistribution functions to bssm. Specify that the state disturbance distribution is multivariate Student's $t$ with unknown degrees of freedom.

PriorMdl = bssm(@paramMap,@priorDistribution,StateDistribution="t");

PriorMdl is a bssm object representing the Bayesian state-space model with unknown parameters.

In Local Functions, write a function called posteriorDrawsNuU that accepts the input structure and returns the posterior draws of $ν_{u}$ .

function StateDoF = posteriorDrawsStateDoF(inputstruct)
    StateDoF = inputstruct.StateDoF;
end

Simulate draws from the posterior distribution of $Θ, ν_{u} | y$ by using simulate. Specify a random set of positive values in [0,1] to initialize the Kalman filter.

Set the burn-in period of the MCMC algorithm to 1000 draws, draw a sample of 10000 from the posterior, specify the univariate treatment of multivariate series for faster computations, and set the proposal scale matrix to a diagonal matrix with small values along the diagonal to increase the proposal acceptance rate.

numParamsTheta = 4;
theta0 = rand(numParamsTheta,1);
[ThetaPostDraws,accept,StateDoFDraws] = simulate(PriorMdl,y,theta0, ...
    eye(numParamsTheta)/1000,BurnIn=1e3,NumDraws=1e4, ...
    Univariate=true,OutputFunction=@posteriorDrawsStateDoF);

[numThetaParams,numDraws] = size(ThetaPostDraws)

numThetaParams = 
4

numDraws = 
10000

accept

accept = 
0.4066

size(StateDoFDraws)

ans = 1×2

           1       10000

ThetaPostDraws is a 4-by-10000 matrix containing the posterior draws of the parameters $Θ$ . accept is the Metropolis-Hastings sampler acceptance probability, in this case 41%, which means that simulate rejected 59% of the posterior draws. StateDoFDraws is a 1-by-10000 vector containing the posterior draws of $ν_{u}$ .

To diagnose the Markov chain induced by the Metropolis-within-Gibbs sampler, create a trace plot of the posterior draws of $ν_{u}$ .

figure
plot(StateDoFDraws)
title("Posterior Trace Plot of \nu_u")

Figure contains an axes object. The axes object with title Posterior Trace Plot of nu indexOf u baseline contains an object of type line.

The posterior sample shows significant serial correlation. You can remedy these behaviors by adjusting the Thin name-value argument. In general, simulate has name-value arguments that enable you to control several aspects of the MCMC sampler, which can improve the quality of the posterior sample.

Local Functions

This example uses the following functions. paramMap is the parameter-to-matrix mapping function and priorDistribution is the log prior distribution of the parameters.

function [A,B,C,D,Mean0,Cov0,StateType] = paramMap(theta)
    A = [theta(1) 0; 0 theta(2)];
    B = [theta(3) 0; 0 theta(4)];
    C = [1 3];
    D = 0;
    Mean0 = [];         % MATLAB uses default initial state mean
    Cov0 = [];          % MATLAB uses initial state covariances
    StateType = [0; 0]; % Two stationary states
end

function logprior = priorDistribution(theta)
    paramconstraints = [(abs(theta(1)) >= 1) (abs(theta(2)) >= 1) ...
        (theta(3) < 0) (theta(4) < 0)];
    if(sum(paramconstraints))
        logprior = -Inf;
    else 
        mu0 = 0.5*ones(numel(theta),1); 
        sigma0 = 1;
        p = normpdf(theta,mu0,sigma0);
        logprior = sum(log(p));
    end
end

function StateDoF = posteriorDrawsStateDoF(inputstruct)
    StateDoF = inputstruct.StateDoF;
end

Input Arguments

collapse all

`PriorMdl` — Prior Bayesian state-space model
`bssm` model object

Prior Bayesian state-space model, specified as a bssm model object return by bssm or ssm2bssm.

The function handles of the properties PriorMdl.ParamDistribution and PriorMdl.ParamMap determine the prior and the data likelihood, respectively.

`Y` — Observed response data
numeric matrix | cell vector of numeric vectors

Observed response data, from which simulate forms the posterior distribution, specified as a numeric matrix or a cell vector of numeric vectors.

If PriorMdl is time invariant with respect to the observation equation, Y is a T-by-n matrix. Each row of the matrix corresponds to a period and each column corresponds to a particular observation in the model. T is the sample size and n is the number of observations per period. The last row of Y contains the latest observations.
If PriorMdl is time varying with respect to the observation equation, Y is a T-by-1 cell vector. Y{t} contains an n_t-dimensional vector of observations for period t, where t = 1, ..., T. The corresponding dimensions of the coefficient matrices, outputs of PriorMdl.ParamMap, C{t}, and D{t} must be consistent with the matrix in Y{t} for all periods. The last cell of Y contains the latest observations.

NaN elements indicate missing observations. For details on how the Kalman filter accommodates missing observations, see Algorithms.

Data Types: double | cell

`params0` — Initial values for parameters Θ
numeric vector

Initial parameter values for the parameters Θ, specified as a numParams-by-1 numeric vector. Elements of params0 must correspond to the elements of the first input arguments of PriorMdl.ParamMap and PriorMdl.ParamDistribution.

Data Types: double

`Proposal` — MH sampler proposal distribution covariance/scale matrix for parameters Θ
positive definite numeric matrix

MH sampler proposal distribution covariance/scale matrix for the parameters Θ, up to the proportionality constant Proportion, specified as a numParams-by-numParams, positive-definite numeric matrix. Elements of Proposal must correspond to elements in params0.

The proposal distribution is multivariate normal or Student's t with DoF degrees of freedom (for details, see DoF).

Data Types: double

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: simulate(Mdl,Y,params0,Proposal,NumDraws=1e6,Thin=3,DoF=10) uses the multivariate t₁₀ distribution for the Metropolis-Hastings proposal, draws 3e6 random vectors of parameters, and thins the sample to reduce serial correlation by discarding every 2 draws until it retains 1e6 draws.

Kalman Filter Options

collapse all

`Univariate` — Univariate treatment of multivariate series flag
`false` (default) | `true`

Univariate treatment of a multivariate series flag, specified as a value in this table.

Value	Description
`true`	Applies the univariate treatment of a multivariate series, also known as sequential filtering
`false`	Does not apply sequential filtering

The univariate treatment can accelerate and improve numerical stability of the Kalman filter. However, all observation innovations must be uncorrelated. That is, D_tD_t' must be diagonal, where D_t (t = 1, ..., T) is the output coefficient matrix D of PriorMdl.ParamMap and PriorMdl.ParamDistribution.

Example: Univariate=true

Data Types: logical

`SquareRoot` — Square root filter method flag
`false` (default) | `true`

Square root filter method flag, specified as a value in this table.

Value	Description
`true`	Applies the square root filter method for the Kalman filter
`false`	Does not apply the square root filter method

If you suspect that the eigenvalues of the filtered state or forecasted observation covariance matrices are close to zero, then specify SquareRoot=true. The square root filter is robust to numerical issues arising from the finite precision of calculations, but requires more computational resources.

Example: SquareRoot=true

Data Types: logical

Posterior Sampling Options

collapse all

`NumDraws` — Number of Metropolis-Hastings sampler draws
`1000` (default) | positive integer

Number of Metropolis-Hastings sampler draws from the posterior distribution Π(θ|Y), specified as a positive integer.

Example: NumDraws=1e7

Data Types: double

`BurnIn` — Number of draws to remove from beginning of sample
`100` (default) | nonnegative scalar

Number of draws to remove from the beginning of the sample to reduce transient effects, specified as a nonnegative scalar. For details on how simulate reduces the full sample, see Algorithms.

Tip

To help you specify the appropriate burn-in period size:

Determine the extent of the transient behavior in the sample by setting the BurnIn name-value argument to 0.
Simulate a few thousand observations by using simulate.
Create trace plots.

Example: BurnIn=1000

Data Types: double

`Thin` — Adjusted sample size multiplier
`1` (no thinning) (default) | positive integer

Adjusted sample size multiplier, specified as a positive integer.

The actual sample size is BurnIn + NumDraws*Thin. After discarding the burn-in, simulate discards every Thin – 1 draws, and then retains the next draw. For more details on how simulate reduces the full sample, see Algorithms.

Tip

To reduce potential large serial correlation in the posterior sample, or to reduce the memory consumption of the output sample, specify a large value for Thin.

Example: Thin=5

Data Types: double

`DoF` — Proposal distribution degrees of freedom
`Inf` (default) | positive scalar

Proposal distribution degrees of freedom for parameter updates using the MH sampler, specified as a value in this table.

Value	MH Proposal Distribution
Positive scalar	Multivariate t with `DoF` degrees of freedom
`Inf`	Multivariate normal

The following options specify other aspects of the proposal distribution:

Proposal — Required covariance/scale matrix
Proportion — Optional proportionality constant that scales Proposal
Center — Optional expected value
StdDoF — Optional proposal standard deviation of the degrees of freedom parameter of the t-distributed state disturbance or observation innovation process

Example: DoF=10

Data Types: double

`Proportion` — Proposal scale matrix proportionality constant
`1` (default) | positive scalar

Proposal scale matrix proportionality constant, specified as a positive scalar.

Tip

For higher proposal acceptance rates, experiment with relatively small values for Proportion.

Example: Proportion=1

Data Types: double

`Center` — Proposal distribution center
`[]` (default) | numeric vector

Proposal distribution center, specified as a value in this table.

Value	Description
`numParams`-by-1 numeric vector	`simulate` uses the independence Metropolis-Hastings sampler. `Center` is the center of the proposal distribution.
`[]` (empty array)	`simulate` uses the random-walk Metropolis-Hastings sampler. The center of the proposal density is the current state of the Markov chain.

Example: Center=ones(10,1)

Data Types: double

`StdDoF` — Proposal standard deviation for degrees of freedom parameter
`0.1` (default) | positive numeric scalar

Proposal standard deviation for the degrees of freedom parameter of the t-distributed state disturbance or observation innovation process, specified as a positive numeric scalar.

StdDoF applies to the corresponding process when PriorMdl.StateDistribution.Name is "t" or PriorMdl.ObservationDistribution.Name is "t", and their associated degrees of freedom are estimable (the DoF field is NaN or a function handle). For example, if the following conditions hold, StdDof applies only to the t-distribution degrees of freedom of the state disturbance process:

PriorMdl.StateDistribution.Name is "t".
PriorMdl.StateDistribution.DoF is NaN.
The limiting distribution of the observation innovations is Gaussian (PriorMdl.ObservationDistribution.Name is "Gaussian" or PriorMdl.ObservationDistribution is struct("Name","t","DoF",Inf).

Example: StdDoF=0.5

Data Types: double

`OutputFunction` — Function to call after each MCMC iteration
`[]` (default) | function handle

Function that simulate calls after each MCMC iteration, specified as a function handle. simulate saves the outputs of the specified function after each iteration and returns them in the Output output argument. You write the function, which can perform arbitrary calculations, such as computing or plotting custom statistics at each iteration.

Suppose outputfcn is the name of the MATLAB^® function associated with specified function handle. outputfcn must have this form.

function Output = outputfcn(Input)
	...
end

At each iteration, simulate passes Input as a structure array with fields in this table. In other words, values in this table are available for operations in the function.

Field	Description	Value
`Iteration`	Current iteration	Numeric scalar
`Parameters`	Current values of the parameters θ	Numeric vector
`LogPosteriorDensity`	Log posterior density evaluated at current parameters and conditioned on latent variables	Numeric scalar
`StateDoF`	Current degree of freedom of the t-distributed state disturbances	Numeric scalar
`ObservationDoF`	Current degree of freedom of the t-distributed observation innovation	Numeric scalar
`StateVariance`	Current latent variance variable associated with the state disturbance	T-by-1 numeric vector
`ObservationVariance`	Current latent variance variable associated with the observation innovation	T-by-1 numeric vector
`Mixture`	Gaussian mixture distribution hyperparameters for finite Gaussian mixture observation innovations	Structure array equal to `PriorMdl.ObservationDistribution`
`LatentClass`	Current latent regime variable for finite-Gaussian-mixture observation innovations	T-by-1 numeric vector
`Intercept`	Current observation deflator factor for finite-Gaussian-mixture or skew-normal observation innovations	T-by-1 numeric vector
`Delta`	Current shape hyperparameter δ for skew normal observation innovations	Numeric scalar
`A`	Coefficient A evaluated at current parameters	Numeric matrix for a dimension-invariant coefficient or a T-by-1 cell vector of numeric matrices for a dimension-varying coefficient
`B`	Coefficient B evaluated at current parameters	Numeric matrix for a dimension-invariant coefficient or a T-by-1 cell vector of numeric matrices for a dimension-varying coefficient
`C`	Coefficient C evaluated at current parameters	Numeric matrix for a dimension-invariant coefficient or a T-by-1 cell vector of numeric matrices for a dimension-varying coefficient
`D`	Coefficient D evaluated at current parameters	Numeric matrix for a dimension-invariant coefficient or a T-by-1 cell vector of numeric matrices for a dimension-varying coefficient
`States`	Current state draws obtained by simulation smoother	Numeric matrix for a dimension-invariant coefficient or a T-by-1 cell vector of numeric matrices for a dimension-varying coefficient
`Y`	Observations	The value of the input `Y`
`PreviousOutput`	Output of the previous iteration	Structure array with fields in this table

Output depends on the computations in outputfcn. However, if Output is a k-by-1 homogeneous column vector, simulate concatenates the outputs of all iterations and returns a k-by-NumDraws matrix of the same type. If simulate cannot horizontally concatenate the outputs of all iterations, simulate returns a 1-by-NumDraws cell array instead, where successive cells contain the output of corresponding iterations.

Example: OutputFunction=@outputfcn

Data Types: function_handle

Output Arguments

collapse all

`Params` — Posterior draws
numeric matrix

Posterior draws of the state-space model parameters Θ, returned as a numParams-by-NumDraws numeric matrix. Each column is a separate draw from the distribution. Each row corresponds to the corresponding element of params0.

Because the MH sampler is a Markov chain, successive draws are correlated.

`accept` — Proposal acceptance rate
positive scalar in [0,1]

Proposal acceptance rate, returned as a positive scalar in [0,1].

`Output` — Custom function output
array

Custom function OutputFunction output concatenated over all MCMC iterations, returned as a matrix or cell vector. Output has NumDraws columns, and the number of rows depends on the size of the output at each iteration. The data type of the entries of Output depends on the operations of the output function.

More About

collapse all

Latent Variance Variables of t-Distributed Errors

To facilitate posterior sampling, multivariate Student's t-distributed state disturbances and observation innovations are each represented as an inverse-gamma scale mixture, where the inverse-gamma random variable is the latent variance variable.

Explicitly, suppose the m-dimensional state disturbances u_t are iid multivariate t distributed with location 0, scale I_m, and degrees of freedom ν_u. As an inverse-gamma scale mixture

$u_{t} = \sqrt{ζ_{t}} {\tilde{u}}_{t},$

where:

The latent variable ζ_t is inverse-gamma with shape and scale ν_u/2.
${\tilde{u}}_{t}$ is an m-dimensional multivariate standard Gaussian random variable.

Multivariate t-distributed observation innovations can be similarly decomposed.

You can access ζ_t by writing a custom output function that returns the field for the specified error type, either StateVariance or ObservationVariance. For more details, see the OutputFunction name-value argument and Output output argument.

Latent Regime Variable of Finite-Gaussian-Mixture-Distributed Observation Innovations

The latent regime variable z_t is a discrete random variable that describes the probability distribution of randomly selecting one of the r regimes of the Gaussian mixture distribution. It is a latent component of a hierarchical representation of finite-Gaussian-mixture-distributed observation innovations ε_t. The sample space of z_t is 1,…,r and P(z_t = j) = w_j, where w_j = PriorMdl.Distribution.Weight(j).

Suppose univariate ε_t is a series of iid finite Gaussian mixture distributed random variables with r regimes, weight or probability vector w, mean vector μ, and variance vector σ². At time t and given z_t = j, ε_t has a Gaussian distribution with mean μ_j and variance σ²_j. Therefore, the distribution of ε_t is

$p (ε_{t}) = \int_{z_{t}} p_{Z_{t}} (z) p_{ε_{t} | z_{t}} (ε_{t} | z_{t}) d z = \sum_{j = 1}^{r} w_{j} ϕ (μ_{j}, σ_{j}^{2}; ε_{t}) .$

bssm functions use this representation to facilitate posterior sampling from $p (θ, x, z | y)$ by the Metropolis-within-Gibbs sampler:

Condition on z_t = j and y_t and use the results of the Kalman filter to sample from

$p (θ, x | y, z) = p (θ | y, z) p (x | y, θ, z) .$
1. Evaluate $p (θ | y, z) \propto p (θ) p (y | θ, z),$ where p(θ) is the prior specified by PriorMdl and p(y_t|θ,z_t) is a result of the Kalman filter.
2. Update θ using the Metropolis-Hastings sampler.
3. Update the states according to p(x_t|θ,y_t,z_t) by using the simulation smoother.
Update z_t from a categorical distribution according to $p (z | θ, y, x) .$

You can access z_t by writing a custom output function that returns the LatentClass field. For more details, see the OutputFunction name-value argument and Output output argument.

Observation Deflators In Finite-Gaussian-mixture and Skew-Normal Observation-Innovation Models

In general, an observation deflator factor d_t in a state-space model is a factor in the term subtracted from the observation y_t to ensure the mean of the observation equation, re-expressed in terms of the deflated observation ${\tilde{y}}_{t},$ is C_tx_t. This deflation helps identify the states in the observation equation for state and parameter estimation.

bssm functions deflate observations when the observation innovation variable ε_t has one of the following distributions:

Finite Gaussian mixture — For a given latent class z_t = j, d_t = μ_j.
Skew normal — $d_{t} = δ (\frac{δ}{δ^{2} + 1} {\tilde{ε}}_{t} + \frac{1}{\sqrt{δ^{2} + 1}} ζ_{α_{t}}),$ where ${\tilde{ε}}_{t}$ are the series of residuals scaled by D_t and ζ_{ɑ_t} is a randomly drawn value from the truncated normal distribution, with support (0,∞), derived from a Gaussian distribution with a mean of $\frac{δ}{δ^{2} + 1} {\tilde{ε}}_{t}$ and a variance of $\frac{1}{δ^{2} + 1}$ (simulate determines the intercept during posterior sampling).

Regardless of observation-innovation distribution, simulate deflates the observations by $\tilde{y} = y_{t} - D_{t} d_{t}$ . You can access d_t by writing a custom output function that returns the Intercept field. For more details, see the OutputFunction name-value argument and Output output argument.

Tips

Acceptance rates from accept that are relatively close to 0 or 1 indicate that the Markov chain does not sufficiently explore the posterior distribution. To obtain an appropriate acceptance rate for your data, tune the sampler by implementing one of the following procedures.
- Use the tune function to search for the posterior mode by numerical optimization. tune returns optimized parameters and the proposal scale matrix, which is proportional to the negative Hessian matrix evaluated at the posterior mode. Pass the optimized parameters and the proposal scale to simulate, and tune the proportionality constant by using the Proportion name-value argument. Small values of Proportion tend to increase the proposal acceptance rates of the MH sampler.
- Perform a multistage simulation:
  1. Choose an initial value for the input Proposal and simulate draws from the posterior.
  2. Compute the sample covariance matrix, and pass the result to simulate as an updated value for Proposal.
  3. Repeat steps 1 and 2 until accept is reasonable for your data.

Algorithms

simulate performs posterior simulation of model parameters, states, and latent variables as follows:
1. simulate generates parameter draws by the Metropolis-Hastings sampler. The posterior density is proportional to the product of the prior density PriorMdl.ParamDistribution and the likelihood obtained by the Kalman filter of the state-space model PriorMdl.ParamMap.
2. simulate updates states by the simulation smoother of the state-space model.
3. simulate samples the latent variance variables of state disturbance and observation innovation distributions from posterior conditional distributions. For t-distributed state disturbances or observation innovations, latent variables are inverse-gamma distributed.
If the input prior model PrioirMdl is a Gaussian linear state-space model and you do not specify the custom output function OutputFunction, simulate marginalizes the states, and the Metropolis-Hastings sampler simulates only parameters. Otherwise, simulate simulates parameters Θ, states x_t, and latent variables ζ_t by the Metropolis-within-Gibbs sampler, which is more computationally intensive compared to the standard Metropolis-Hastings sampler.
This figure shows how simulate reduces the sample by using the values of NumDraws, Thin, and BurnIn. Rectangles represent successive draws from the distribution. simulate removes the white rectangles from the sample. The remaining NumDraws black rectangles compose the sample.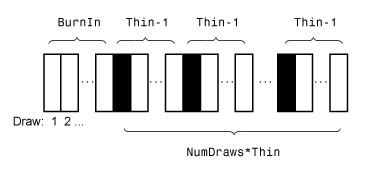

References

[1] Hastings, Wilfred K. "Monte Carlo Sampling Methods Using Markov Chains and Their Applications." Biometrika 57 (April 1970): 97–109. https://doi.org/10.1093/biomet/57.1.97.

[2] Metropolis, Nicholas, Rosenbluth, Arianna. W., Rosenbluth, Marshall. N., Teller, Augusta. H., and Teller, Edward. "Equation of State Calculations by Fast Computing Machines." The Journal of Chemical Physics 21 (June 1953): 1087–92. https://doi.org/10.1063/1.1699114.

Version History

Introduced in R2022a

simulate

Syntax

Description

Examples

Draw Random Parameters from Posterior Distribution of Time-Invariant Model

Improve Markov Chain Convergence

Simulate Parameters from Posterior of Time-Varying Model

Draw Posterior Sample From Model with Deflated Response

Access Degrees of Freedom Posterior Draws Using Output Function

Input Arguments

PriorMdl — Prior Bayesian state-space model bssm model object

Y — Observed response data numeric matrix | cell vector of numeric vectors

params0 — Initial values for parameters Θ numeric vector

Proposal — MH sampler proposal distribution covariance/scale matrix for parameters Θ positive definite numeric matrix

Name-Value Arguments

Univariate — Univariate treatment of multivariate series flag false (default) | true

SquareRoot — Square root filter method flag false (default) | true

NumDraws — Number of Metropolis-Hastings sampler draws 1000 (default) | positive integer

BurnIn — Number of draws to remove from beginning of sample 100 (default) | nonnegative scalar

Thin — Adjusted sample size multiplier 1 (no thinning) (default) | positive integer

DoF — Proposal distribution degrees of freedom Inf (default) | positive scalar

Proportion — Proposal scale matrix proportionality constant 1 (default) | positive scalar

Center — Proposal distribution center [] (default) | numeric vector

StdDoF — Proposal standard deviation for degrees of freedom parameter 0.1 (default) | positive numeric scalar

OutputFunction — Function to call after each MCMC iteration [] (default) | function handle

Output Arguments

Params — Posterior draws numeric matrix

accept — Proposal acceptance rate positive scalar in [0,1]

Output — Custom function output array

More About

Latent Variance Variables of t-Distributed Errors

Latent Regime Variable of Finite-Gaussian-Mixture-Distributed Observation Innovations

Observation Deflators In Finite-Gaussian-mixture and Skew-Normal Observation-Innovation Models

Tips

Algorithms

References

Version History

See Also

Objects

Functions

Topics

`PriorMdl` — Prior Bayesian state-space model
`bssm` model object

`Y` — Observed response data
numeric matrix | cell vector of numeric vectors

`params0` — Initial values for parameters Θ
numeric vector

`Proposal` — MH sampler proposal distribution covariance/scale matrix for parameters Θ
positive definite numeric matrix

`Univariate` — Univariate treatment of multivariate series flag
`false` (default) | `true`

`SquareRoot` — Square root filter method flag
`false` (default) | `true`

`NumDraws` — Number of Metropolis-Hastings sampler draws
`1000` (default) | positive integer

`BurnIn` — Number of draws to remove from beginning of sample
`100` (default) | nonnegative scalar

`Thin` — Adjusted sample size multiplier
`1` (no thinning) (default) | positive integer

`DoF` — Proposal distribution degrees of freedom
`Inf` (default) | positive scalar

`Proportion` — Proposal scale matrix proportionality constant
`1` (default) | positive scalar

`Center` — Proposal distribution center
`[]` (default) | numeric vector

`StdDoF` — Proposal standard deviation for degrees of freedom parameter
`0.1` (default) | positive numeric scalar

`OutputFunction` — Function to call after each MCMC iteration
`[]` (default) | function handle

`Params` — Posterior draws
numeric matrix

`accept` — Proposal acceptance rate
positive scalar in [0,1]

`Output` — Custom function output
array