simulate

Simulate regression coefficients and disturbance variance of Bayesian linear regression model

Syntax

[BetaSim,sigma2Sim]
= simulate(Mdl)

[BetaSim,sigma2Sim]
= simulate(Mdl,X,y)

[BetaSim,sigma2Sim]
= simulate(___,Name,Value)

[BetaSim,sigma2Sim,RegimeSim] 
= simulate(___)

Description

[BetaSim,sigma2Sim] = simulate(Mdl) returns a random vector of regression coefficients (BetaSim) and a random disturbance variance (sigma2Sim) drawn from the Bayesian linear regression model Mdl of β and σ².

If Mdl is a joint prior model (returned by bayeslm), then simulate draws from the prior distributions.
If Mdl is a joint posterior model (returned by estimate), then simulate draws from the posterior distributions.

example

[BetaSim,sigma2Sim] = simulate(Mdl,X,y) draws from the marginal posterior distributions produced or updated by incorporating the predictor data X and corresponding response data y.

If Mdl is a joint prior model, then simulate produces the marginal posterior distributions by updating the prior model with information about the parameters that it obtains from the data.
If Mdl is a marginal posterior model, then simulate updates the posteriors with information about the parameters that it obtains from the additional data. The complete data likelihood is composed of the additional data X and y, and the data that created Mdl.

NaNs in the data indicate missing values, which simulate removes by using list-wise deletion.

example

[BetaSim,sigma2Sim] = simulate(___,Name,Value) uses any of the input argument combinations in the previous syntaxes and additional options specified by one or more name-value pair arguments. For example, you can specify a value for β or σ² to simulate from the conditional posterior distribution of one parameter, given the specified value of the other parameter.

example

[BetaSim,sigma2Sim,RegimeSim] = simulate(___) also returns draws from the latent regime distribution if Mdl is a Bayesian linear regression model for stochastic search variable selection (SSVS), that is, if Mdl is a mixconjugateblm or mixsemiconjugateblm model object.

example

Examples

collapse all

Simulate Parameter Value from Prior and Posterior Distributions

Open Live Script

Consider the multiple linear regression model that predicts the US real gross national product (GNPR) by using a linear combination of industrial production index (IPI), total employment (E), and real wages (WR).

${GNPR}_{t} = β_{0} + β_{1} {IPI}_{t} + β_{2} E_{t} + β_{3} {WR}_{t} + ε_{t} .$

For all $t$ , $ε_{t}$ is a series of independent Gaussian disturbances with a mean of 0 and variance $σ^{2}$ .

Assume these prior distributions:

$β | σ^{2} \sim N_{4} (M, σ^{2} V)$ . $M$ is a 4-by-1 vector of means, and $V$ is a scaled 4-by-4 positive definite covariance matrix.
$σ^{2} \sim I G (A, B)$ . $A$ and $B$ are the shape and scale, respectively, of an inverse gamma distribution.

These assumptions and the data likelihood imply a normal-inverse-gamma conjugate model.

Load the Nelson-Plosser data set. Create variables for the response and predictor series.

load Data_NelsonPlosser
varNames = {'IPI' 'E' 'WR'};
X = DataTable{:,varNames};
y = DataTable{:,'GNPR'};

Create a normal-inverse-gamma conjugate prior model for the linear regression parameters. Specify the number of predictors p and the variable names.

p = 3;
PriorMdl = bayeslm(p,'ModelType','conjugate','VarNames',varNames);

PriorMdl is a conjugateblm Bayesian linear regression model object representing the prior distribution of the regression coefficients and disturbance variance.

Simulate a set of regression coefficients and a value of the disturbance variance from the prior distribution.

rng(1); % For reproducibility
[betaSimPrior,sigma2SimPrior] = simulate(PriorMdl)

betaSimPrior = 4×1

  -33.5917
  -49.1445
  -37.4492
  -25.3632

sigma2SimPrior = 
0.1962

betaSimPrior is the randomly drawn 4-by-1 vector of regression coefficients corresponding to the names in PriorMdl.VarNames. The sigma2SimPrior output is the randomly drawn scalar disturbance variance.

Estimate the posterior distribution.

PosteriorMdl = estimate(PriorMdl,X,y);

Method: Analytic posterior distributions
Number of observations: 62
Number of predictors:   4
Log marginal likelihood: -259.348
 
           |   Mean      Std          CI95        Positive       Distribution      
-----------------------------------------------------------------------------------
 Intercept | -24.2494  8.7821  [-41.514, -6.985]    0.003   t (-24.25, 8.65^2, 68) 
 IPI       |   4.3913  0.1414   [ 4.113,  4.669]    1.000   t (4.39, 0.14^2, 68)   
 E         |   0.0011  0.0003   [ 0.000,  0.002]    1.000   t (0.00, 0.00^2, 68)   
 WR        |   2.4683  0.3490   [ 1.782,  3.154]    1.000   t (2.47, 0.34^2, 68)   
 Sigma2    |  44.1347  7.8020   [31.427, 61.855]    1.000   IG(34.00, 0.00069)

PosteriorMdl is a conjugateblm Bayesian linear regression model object representing the posterior distribution of the regression coefficients and disturbance variance.

Simulate a set of regression coefficients and a value of the disturbance variance from the posterior distribution.

[betaSimPost,sigma2SimPost] = simulate(PosteriorMdl)

betaSimPost = 4×1

  -25.9351
    4.4379
    0.0012
    2.4072

sigma2SimPost = 
41.9575

betaSimPost and sigma2SimPost have the same dimensions as betaSimPrior and sigma2SimPrior, respectively, but are drawn from the posterior.

Implement Gibbs Sampler for Posterior Estimation

Open Live Script

Consider the regression model in Simulate Parameter Value from Prior and Posterior Distributions.

Load the data and create a conjugate prior model for the regression coefficients and the disturbance variance. Then, estimate the posterior distribution and return the estimation summary table.

load Data_NelsonPlosser
varNames = {'IPI' 'E' 'WR'};
X = DataTable{:,varNames};
y = DataTable{:,'GNPR'};
p = 3;
PriorMdl = bayeslm(p,'ModelType','conjugate','VarNames',varNames);
[PosteriorMdl,Summary] = estimate(PriorMdl,X,y);

Method: Analytic posterior distributions
Number of observations: 62
Number of predictors:   4
Log marginal likelihood: -259.348
 
           |   Mean      Std          CI95        Positive       Distribution      
-----------------------------------------------------------------------------------
 Intercept | -24.2494  8.7821  [-41.514, -6.985]    0.003   t (-24.25, 8.65^2, 68) 
 IPI       |   4.3913  0.1414   [ 4.113,  4.669]    1.000   t (4.39, 0.14^2, 68)   
 E         |   0.0011  0.0003   [ 0.000,  0.002]    1.000   t (0.00, 0.00^2, 68)   
 WR        |   2.4683  0.3490   [ 1.782,  3.154]    1.000   t (2.47, 0.34^2, 68)   
 Sigma2    |  44.1347  7.8020   [31.427, 61.855]    1.000   IG(34.00, 0.00069)

Summary is a table containing the statistics that estimate displays at the command line.

Although the marginal and conditional posterior distributions of $β$ and $σ^{2}$ are analytically tractable, this example focuses on how to implement the Gibbs sampler to reproduce known results.

Estimate the model again, but use a Gibbs sampler. Alternate between sampling from the conditional posterior distributions of the parameters. Sample 10,000 times and create variables for preallocation. Start the sampler by drawing from the conditional posterior of $β$ given $σ^{2} = 2$ .

m = 1e4;
BetaDraws = zeros(p + 1,m);
sigma2Draws = zeros(1,m + 1);
sigma2Draws(1) = 2;
rng(1); % For reproducibility
for j = 1:m
    BetaDraws(:,j) = simulate(PriorMdl,X,y,'Sigma2',sigma2Draws(j));
    [~,sigma2Draws(j + 1)] = simulate(PriorMdl,X,y,'Beta',BetaDraws(:,j));
end
sigma2Draws = sigma2Draws(2:end); % Remove initial value from MCMC sample

Graph trace plots of the parameters.

figure;
for j = 1:(p + 1);
    subplot(2,2,j);
    plot(BetaDraws(j,:))
    ylabel('MCMC Draw')
    xlabel('Simulation Index')
    title(sprintf('Trace Plot — %s',PriorMdl.VarNames{j}));
end

figure;
plot(sigma2Draws)
ylabel('MCMC Draw')
xlabel('Simulation Index')
title('Trace plot — Sigma2')

Figure contains an axes object. The axes object with title Trace plot — Sigma2, xlabel Simulation Index, ylabel MCMC Draw contains an object of type line.

The Markov chain Monte Carlo (MCMC) samples appear to converge and mix well.

Apply a burn-in period of 1000 draws, and then compute the means and standard deviations of the MCMC samples. Compare them with the estimates from estimate.

bp = 1000;
postBetaMean = mean(BetaDraws(:,(bp + 1):end),2);
postSigma2Mean = mean(sigma2Draws(:,(bp + 1):end));
postBetaStd = std(BetaDraws(:,(bp + 1):end),[],2);
postSigma2Std = std(sigma2Draws((bp + 1):end));
[Summary(:,1:2),table([postBetaMean; postSigma2Mean],...
    [postBetaStd; postSigma2Std],'VariableNames',{'GibbsMean','GibbsStd'})]

ans=5×4 table
                   Mean          Std        GibbsMean     GibbsStd 
                 _________    __________    _________    __________

    Intercept      -24.249        8.7821      -24.293         8.748
    IPI             4.3913        0.1414       4.3917       0.13941
    E            0.0011202    0.00032931    0.0011229    0.00032875
    WR              2.4683       0.34895       2.4654       0.34364
    Sigma2          44.135         7.802       44.011        7.7816

The estimates are very close. MCMC variations account for the differences.

Simulate Regimes from SSVS Predictor Selection

Open Live Script

Consider the regression model in Simulate Parameter Value from Prior and Posterior Distributions.

Assume these prior distributions for $k$ = 0,...,3:

$β_{k} | σ^{2}, γ_{k} = γ_{k} σ \sqrt{V_{k 1}} Z_{1} + (1 - γ_{k}) σ \sqrt{V_{k 2}} Z_{2}$ , where $Z_{1}$ and $Z_{2}$ are independent, standard normal random variables. Therefore, the coefficients have a Gaussian mixture distribution. Assume all coefficients are conditionally independent, a priori, but they are dependent on the disturbance variance.
$σ^{2} \sim I G (A, B)$ . $A$ and $B$ are the shape and scale, respectively, of an inverse gamma distribution.
$γ_{k} \in {0, 1}$ and it represents the random variable-inclusion regime variable with a discrete uniform distribution.

Create a prior model for performing SSVS. Assume that $β$ and $σ^{2}$ are dependent (a conjugate mixture model). Specify the number of predictors p and the names of the regression coefficients.

p = 3;
PriorMdl = mixconjugateblm(p,'VarNames',["IPI" "E" "WR"]);

Load the Nelson-Plosser data set. Create variables for the response and predictor series.

load Data_NelsonPlosser
X = DataTable{:,PriorMdl.VarNames(2:end)};
y = DataTable{:,'GNPR'};

Compute the number of possible regimes, that is, number of combinations that result from including and excluding variables in the model.

cardRegime = 2^(PriorMdl.Intercept + PriorMdl.NumPredictors)

cardRegime = 
16

Simulate 10,000 regimes from the posterior distribution.

rng(1);
[~,~,RegimeSim] = simulate(PriorMdl,X,y,'NumDraws',10000);

RegimeSim is a 4-by-1000 logical matrix. Rows correspond to the variables in Mdl.VarNames, and columns correspond to draws from the posterior distribution.

Plot a histogram of the regimes visited. Recode the regimes so that they are readable. Specifically, for each regime, create a string that identifies the variables in the model, and separate the variables with dots.

cRegime = num2cell(RegimeSim,1);
cRegime = categorical(cellfun(@(c)join(PriorMdl.VarNames(c),"."),cRegime));
cRegime(ismissing(cRegime)) = "NoCoefficients";

histogram(cRegime);
title('Variables Included in Models')
ylabel('Frequency');

Figure contains an axes object. The axes object with title Variables Included in Models, ylabel Frequency contains an object of type categoricalhistogram.

Compute the marginal posterior probability of variable inclusion.

table(mean(RegimeSim,2),'RowNames',PriorMdl.VarNames,...
    'VariableNames',"Regime")

ans=4×1 table
                 Regime
                 ______

    Intercept    0.8829
    IPI          0.4547
    E             0.098
    WR           0.1692

Robust Regression Using Gibbs Sampler

Open Live Script

Consider a Bayesian linear regression model containing one predictor, and a t distributed disturbance variance with a profiled degrees of freedom parameter $ν$ .

$λ_{j} \sim I G (ν / 2, 2 / ν)$ .
$ε_{j} | λ_{j} \sim N (0, λ_{j} σ^{2})$
$f (β, σ^{2}) \propto \frac{1}{σ^{2}}$

These assumptions imply:

$ε_{j} \sim t (0, σ^{2}, ν)$
$λ_{j} | ε_{j} \sim I G (\frac{ν + 1}{2}, \frac{2}{ν + ε_{j}^{2} / σ^{2}})$

$λ$ is a vector of latent scale parameters that attributes low precision to observations far from the regression line. $ν$ is a hyperparameter controlling the influence of $λ$ on the observations.

For this problem, the Gibbs sampler is well suited to estimate the coefficients because you can simulate the parameters of a Bayesian linear regression model conditioned on $λ$ , and then simulate $λ$ from its conditional distribution.

Generate $n = 100$ responses from $y_{t} = 1 + 2 x_{t} + e_{t},$ where $x \in [0, 2]$ and $e_{t} \sim N (0, 0 . 5^{2})$ .

rng('default');
n = 100;
x = linspace(0,2,n)';
b0 = 1;
b1 = 2;
sigma = 0.5;
e = randn(n,1);
y = b0 + b1*x + sigma*e;

Introduce outlying responses by inflating all responses below $x = 0.25$ by a factor of 3.

y(x < 0.25) = y(x < 0.25)*3;

Fit a linear model to the data. Plot the data and the fitted regression line.

Mdl = fitlm(x,y)

Mdl = 
Linear regression model:
    y ~ 1 + x1

Estimated Coefficients:
                   Estimate      SE       tStat       pValue  
                   ________    _______    ______    __________

    (Intercept)     2.6814     0.28433    9.4304    2.0859e-15
    x1             0.78974     0.24562    3.2153     0.0017653


Number of observations: 100, Error degrees of freedom: 98
Root Mean Squared Error: 1.43
R-squared: 0.0954,  Adjusted R-Squared: 0.0862
F-statistic vs. constant model: 10.3, p-value = 0.00177

figure;
plot(Mdl);
hl = legend;
hold on;

Figure contains an axes object. The axes object with title y vs. x1, xlabel x1, ylabel y contains 3 objects of type line. One or more of the lines displays its values using only markers These objects represent Data, Fit, 95% conf. bounds.

The simulated outliers appear to influence the fitted regression line.

Implement this Gibbs sampler:

Draw parameters from the posterior distribution of $β, σ^{2} | y, x, λ$ . Deflate the observations by $λ$ , create a diffuse prior model with two regression coefficients, and draw a set of parameters from the posterior. The first regression coefficient corresponds to the intercept, so specify that bayeslm not include an intercept.
Compute residuals.
Draw values from the conditional posterior of $λ$ .

Run the Gibbs sampler for 20,000 iterations and apply a burn-in period of 5,000. Specify $ν = 1$ , preallocate for the posterior draws, and initialize $λ$ to a vector of ones.

m = 20000;
nu = 1;
burnin = 5000;
lambda = ones(n,m + 1);
estBeta = zeros(2,m + 1);
estSigma2 = zeros(1,m + 1);
for j = 1:m
    yDef = y./sqrt(lambda(:,j));
    xDef = [ones(n,1) x]./sqrt(lambda(:,j));
    PriorMdl = bayeslm(2,'Model','diffuse','Intercept',false);
    [estBeta(:,j + 1),estSigma2(1,j + 1)] = simulate(PriorMdl,xDef,yDef);
    ep = y - [ones(n,1) x]*estBeta(:,j + 1);
    sp = (nu + 1)/2;
    sc =  2./(nu + ep.^2/estSigma2(1,j + 1));
    lambda(:,j + 1) = 1./gamrnd(sp,sc);
end

A good practice is to diagnose the MCMC sampler by examining trace plots. For brevity, this example skips this task.

Compute the mean of the draws from the posterior of the regression coefficients. Remove the burn-in period draws.

postEstBeta = mean(estBeta(:,(burnin + 1):end),2)

postEstBeta = 2×1

    1.3971
    1.7051

The estimate of the intercept is lower and the slope is higher than the estimates returned by fitlm.

Plot the robust regression line with the regression line fitted by least squares.

h = gca;
xlim = h.XLim';
plotY = [ones(2,1) xlim]*postEstBeta;
plot(xlim,plotY,'LineWidth',2);
hl.String{4} = 'Robust Bayes';

Figure contains an axes object. The axes object with title y vs. x1, xlabel x1, ylabel y contains 4 objects of type line. One or more of the lines displays its values using only markers These objects represent Data, Fit, 95% conf. bounds, Robust Bayes.

The regression line fit using robust Bayesian regression appears to be a better fit.

Estimate Maximum A Posteriori Probability Using Monte Carlo

Open Live Script

The maximum a posteriori probability (MAP) estimate is the posterior mode, that is, the parameter value that yields the maximum of the posterior pdf. If the posterior is analytically intractable, then you can use Monte Carlo sampling to estimate the MAP.

Consider the linear regression model in Simulate Parameter Value from Prior and Posterior Distributions.

Load the Nelson-Plosser data set. Create variables for the response and predictor series.

load Data_NelsonPlosser
varNames = {'IPI' 'E' 'WR'};
X = DataTable{:,varNames};
y = DataTable{:,'GNPR'};

Create a normal-inverse-gamma conjugate prior model for the linear regression parameters. Specify the number of predictors p and the variable names.

p = 3;
PriorMdl = bayeslm(p,'ModelType','conjugate','VarNames',varNames)

PriorMdl = 
  conjugateblm with properties:

    NumPredictors: 3
        Intercept: 1
         VarNames: {4x1 cell}
               Mu: [4x1 double]
                V: [4x4 double]
                A: 3
                B: 1

 
           |  Mean     Std            CI95         Positive       Distribution     
-----------------------------------------------------------------------------------
 Intercept |  0      70.7107  [-141.273, 141.273]    0.500   t (0.00, 57.74^2,  6) 
 IPI       |  0      70.7107  [-141.273, 141.273]    0.500   t (0.00, 57.74^2,  6) 
 E         |  0      70.7107  [-141.273, 141.273]    0.500   t (0.00, 57.74^2,  6) 
 WR        |  0      70.7107  [-141.273, 141.273]    0.500   t (0.00, 57.74^2,  6) 
 Sigma2    | 0.5000   0.5000    [ 0.138,  1.616]     1.000   IG(3.00,    1)

Estimate the marginal posterior distributions of $β$ and $σ^{2}$ .

rng(1); % For reproducibility
PosteriorMdl = estimate(PriorMdl,X,y);

Method: Analytic posterior distributions
Number of observations: 62
Number of predictors:   4
Log marginal likelihood: -259.348
 
           |   Mean      Std          CI95        Positive       Distribution      
-----------------------------------------------------------------------------------
 Intercept | -24.2494  8.7821  [-41.514, -6.985]    0.003   t (-24.25, 8.65^2, 68) 
 IPI       |   4.3913  0.1414   [ 4.113,  4.669]    1.000   t (4.39, 0.14^2, 68)   
 E         |   0.0011  0.0003   [ 0.000,  0.002]    1.000   t (0.00, 0.00^2, 68)   
 WR        |   2.4683  0.3490   [ 1.782,  3.154]    1.000   t (2.47, 0.34^2, 68)   
 Sigma2    |  44.1347  7.8020   [31.427, 61.855]    1.000   IG(34.00, 0.00069)

The display includes the marginal posterior distribution statistics.

Extract the posterior mean of $β$ from the posterior model, and extract the posterior covariance of $β$ from the estimation summary returned by summarize.

estBetaMean = PosteriorMdl.Mu;
Summary = summarize(PosteriorMdl);
EstBetaCov = Summary.Covariances{1:(end - 1),1:(end - 1)};

estBetaMean is a 4-by-1 vector representing the mean of the marginal posterior of $β$ . EstBetaCov is a 4-by-4 matrix representing the covariance matrix of the posterior of $β$ .

Draw 10,000 parameter values from the posterior distribution.

rng(1); % For reproducibility
[BetaSim,sigma2Sim] = simulate(PosteriorMdl,'NumDraws',1e5);

BetaSim is a 4-by-10,000 matrix of randomly drawn regression coefficients. sigma2Sim is a 1-by-10,000 vector of randomly drawn disturbance variances.

Transpose and standardize the matrix of regression coefficients. Compute the correlation matrix of the regression coefficients.

estBetaStd = sqrt(diag(EstBetaCov)');
BetaSim = BetaSim';
BetaSimStd = (BetaSim - estBetaMean')./estBetaStd;
BetaCorr = corrcov(EstBetaCov);
BetaCorr = (BetaCorr + BetaCorr')/2; % Enforce symmetry

Because the marginal posterior distributions are known, evaluate the posterior pdf at all simulated values.

betaPDF = mvtpdf(BetaSimStd,BetaCorr,68);
a = 34;
b = 0.00069;
igPDF = @(x,ap,bp)1./(gamma(ap).*bp.^ap).*x.^(-ap-1).*exp(-1./(x.*bp));...
    % Inverse gamma pdf
sigma2PDF = igPDF(sigma2Sim,a,b);

Find the simulated values that maximize the respective pdfs, that is, the posterior modes.

[~,idxMAPBeta] = max(betaPDF);
[~,idxMAPSigma2] = max(sigma2PDF);
betaMAP = BetaSim(idxMAPBeta,:);
sigma2MAP = sigma2Sim(idxMAPSigma2);

betaMAP and sigma2MAP are the MAP estimates.

Because the posterior of $β$ is symmetric and unimodal, the posterior mean and MAP should be the same. Compare the MAP estimate of $β$ with its posterior mean.

table(betaMAP',PosteriorMdl.Mu,'VariableNames',{'MAP','Mean'},...
    'RowNames',PriorMdl.VarNames)

ans=4×2 table
                    MAP         Mean   
                 _________    _________

    Intercept      -24.559      -24.249
    IPI             4.3964       4.3913
    E            0.0011389    0.0011202
    WR              2.4473       2.4683

The estimates are fairly close to one another.

Estimate the analytical mode of the posterior of $σ^{2}$ . Compare it to the estimated MAP of $σ^{2}$ .

igMode = 1/(b*(a+1))

igMode = 
41.4079

sigma2MAP

sigma2MAP = 
41.4075

These estimates are also fairly close.

Input Arguments

collapse all

`Mdl` — Bayesian linear regression model
`conjugateblm` model object | `semiconjugateblm` model object | `diffuseblm` model object | `mixconjugateblm` model object | `lassoblm` model object

Standard Bayesian linear regression model or model for predictor variable selection, specified as a model object in this table.

Model Object	Description
`conjugateblm`	Dependent, normal-inverse-gamma conjugate model returned by `bayeslm` or `estimate`
`semiconjugateblm`	Independent, normal-inverse-gamma semiconjugate model returned by `bayeslm`
`diffuseblm`	Diffuse prior model returned by `bayeslm`
`empiricalblm`	Prior model characterized by samples from prior distributions, returned by `bayeslm` or `estimate`
`customblm`	Prior distribution function that you declare returned by `bayeslm`
`mixconjugateblm`	Dependent, Gaussian-mixture-inverse-gamma conjugate model for SSVS predictor variable selection, returned by `bayeslm`
`mixsemiconjugateblm`	Independent, Gaussian-mixture-inverse-gamma semiconjugate model for SSVS predictor variable selection, returned by `bayeslm`
`lassoblm`	Bayesian lasso regression model returned by `bayeslm`

Note

Typically, model objects returned by estimate represent marginal posterior distributions. When you estimate a posterior by using estimate, if you specify estimation of a conditional posterior, then estimate returns the prior model.
If Mdl is a diffuseblm model, then you must also supply X and y because simulate cannot draw from an improper prior distribution.
If you supply a lassoblm, mixconjugateblm, or mixsemiconjugateblm model object, supply the data X and y, and draw one value from the posterior, then a best practice is to initialize the Gibbs sampler by specifying the BetaStart and Sigma2Start name-value pair arguments.

`X` — Predictor data
numeric matrix

Predictor data for the multiple linear regression model, specified as a numObservations-by-PriorMdl.NumPredictors numeric matrix. numObservations is the number of observations and must be equal to the length of y.

If Mdl is a posterior distribution, then the columns of X must correspond to the columns of the predictor data used to estimate the posterior.

Data Types: double

`y` — Response data
numeric vector

Response data for the multiple linear regression model, specified as a numeric vector with numObservations elements.

Data Types: double

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: 'Sigma2',2 specifies simulating from the conditional posterior distribution of the regression coefficients given the data and the specified disturbance variance of 2.

Options for All Models

collapse all

`NumDraws` — Effective number of draws
`1` (default) | positive integer

Number of draws to sample from the distribution Mdl, specified as the comma-separated pair consisting of 'NumDraws' and a positive integer.

Tip

If Mdl is an empiricalblm or a customblm model object, then a good practice is to specify a burn-in period with BurnIn and a thinning multiplier with Thin. For details on the adjusted sample size, see Algorithms.

Example: 'NumDraws',1e7

Data Types: double

Options for All Models Except Empirical

collapse all

`Beta` — Value of regression coefficients for simulation from conditional distribution of disturbance variance
empty array (`[]`) (default) | numeric column vector

Value of the regression coefficients for simulation from conditional distribution of the disturbance variance, specified as the comma-separated pair consisting of 'Beta' and an (Mdl.Intercept + Mdl.NumPredictors)-by-1 numeric vector. When using a posterior distribution, simulate draws from π(σ²|y,X,β = Beta), where y is y, X is X, and Beta is the value of 'Beta'. If Mdl.Intercept is true, then Beta(1) corresponds to the model intercept. All other values correspond to the predictor variables that compose the columns of X.

You cannot specify Beta and Sigma2 simultaneously.

By default, simulate does not draw from the conditional posterior of σ².

Example: 'Beta',1:3

Data Types: double

`Sigma2` — Value of disturbance variance for simulation from conditional distribution of regression coefficients
empty array (`[]`) (default) | positive numeric scalar

Value of the disturbance variance for simulation from the conditional distribution of the regression coefficients, specified as the comma-separated pair consisting of 'Sigma2' and a positive numeric scalar. When using a posterior distribution, simulate draws from π(β|y,X,Sigma2), where y is y, X is X, and Sigma2 is the value of 'Sigma2'.

You cannot specify Sigma2 and Beta simultaneously.

By default, simulate does not draw from the conditional posterior of β.

Example: 'Sigma2',1

Data Types: double

Options for All Models Except Conjugate and Empirical

collapse all

`BurnIn` — Number of draws to remove from beginning of sample
`0` (default) | nonnegative scalar

Number of draws to remove from the beginning of the sample to reduce transient effects, specified as the comma-separated pair consisting of 'BurnIn' and a nonnegative scalar. For details on how simulate reduces the full sample, see Algorithms.

Tip

To help you specify the appropriate burn-in period size:

Determine the extent of the transient behavior in the sample by specifying 'BurnIn',0.
Simulate a few thousand observations by using simulate.
Draw trace plots.

Example: 'BurnIn',0

Data Types: double

`Thin` — Adjusted sample size multiplier
`1` (default) | positive integer

Adjusted sample size multiplier, specified as the comma-separated pair consisting of 'Thin' and a positive integer.

The actual sample size is BurnIn + NumDraws*Thin. After discarding the burn-in, simulate discards every Thin – 1 draws, and then retains the next draw. For more details on how simulate reduces the full sample, see Algorithms.

Tip

To reduce potential large serial correlation in the sample, or to reduce the memory consumption of the draws stored in PosteriorMdl, specify a large value for Thin.

Example: 'Thin',5

Data Types: double

`BetaStart` — Starting values of regression coefficients for sampler
numeric column vector

Starting values of the regression coefficients for the sampler, specified as the comma-separated pair consisting of 'BetaStart' and a numeric column vector with (Mdl.Intercept + Mdl.NumPredictors) elements. By default, BetaStart is the ordinary least-squares (OLS) estimate.

Tip

A good practice is to run simulate multiple times with different parameter starting values. Verify that your estimates from each run converge to similar values.

Example: 'BetaStart',[1; 2; 3]

Data Types: double

`Sigma2Start` — Starting values of disturbance variance for sampler
positive numeric scalar

Starting values of the disturbance variance for the sampler, specified as the comma-separated pair consisting of 'Sigma2Start' and a positive numeric scalar. By default, Sigma2Start is the OLS residual mean squared error.

Tip

A good practice is to run simulate multiple times with different parameter starting values. Verify that your estimates from each run converge to similar values.

Example: 'Sigma2Start',4

Data Types: double

Options for SSVS Models

collapse all

`RegimeStart` — Starting values of latent regimes for sampler
`true(Mdl.Intercept + Mdl.NumPredictors)` (default) | logical column vector

Starting values of the latent regimes for the sampler, specified as the comma-separated pair consisting of 'RegimeStart' and a logical column vector with (Mdl.Intercept + Mdl.NumPredictors) elements. RegimeStart(k) = true indicates the inclusion of the variable Mdl.VarNames(k), and RegimeStart(k) = false indicates the exclusion of that variable.

Tip

A good practice is to run simulate multiple times using different parameter starting values. Verify that your estimates from each run converge to similar values.

Example: 'RegimeStart',logical(randi([0 1],Mdl.Intercept + Mdl.NumPredictors,1))

Data Types: double

Options for Custom Models

collapse all

`Reparameterize` — Reparameterization of σ² as log(σ²)
`false` (default) | `true`

Reparameterization of σ² as log(σ²) during posterior estimation and simulation, specified as the comma-separated pair consisting of 'Reparameterize' and a value in this table.

Value	Description
`false`	`simulate` does not reparameterize σ².
`true`	`simulate` reparameterizes σ² as log(σ²). `simulate` converts results back to the original scale and does not change the functional form of `PriorMdl.LogPDF`.

Tip

If you experience numeric instabilities during the posterior estimation or simulation of σ², then specify 'Reparameterize',true.

Example: 'Reparameterize',true

Data Types: logical

`Sampler` — MCMC sampler
`'slice'` (default) | `'metropolis'` | `'hmc'`

MCMC sampler, specified as the comma-separated pair consisting of 'Sampler' and a value in this table.

Value	Description
`'slice'`	Slice sampler
`'metropolis'`	Random walk Metropolis sampler
`'hmc'`	Hamiltonian Monte Carlo (HMC) sampler

Tip

To increase the quality of the MCMC draws, tune the sampler.
1. Before calling simulate, specify the tuning parameters and their values by using sampleroptions. For example, to specify the slice sampler width width, use:
  options = sampleroptions('Sampler',"slice",'Width',width);
2. Specify the object containing the tuning parameter specifications returned by sampleroptions by using the 'Options' name-value pair argument. For example, to use the tuning parameter specifications in options, specify:
```
'Options',options
```
If you specify the HMC sampler, then a best practice is to provide the gradient for some variables, at least. simulate resorts the numerical computation of any missing partial derivatives (NaN values) in the gradient vector.

Example: 'Sampler',"hmc"

Data Types: string

`Options` — Sampler options
`[]` (default) | structure array

Sampler options, specified as the comma-separated pair consisting of 'Options' and a structure array returned by sampleroptions. Use 'Options' to specify the MCMC sampler and its tuning-parameter values.

Example: 'Options',sampleroptions('Sampler',"hmc")

Data Types: struct

`Width` — Typical sampling-interval width
positive numeric scalar | numeric vector of positive values

Typical sampling-interval width around the current value in the marginal distributions for the slice sampler, specified as the comma-separated pair consisting of 'Width' and a positive numeric scalar or a (PriorMdl.Intercept + PriorMdl.NumPredictors + 1)-by-1 numeric vector of positive values. The first element corresponds to the model intercept, if one exists in the model. The next PriorMdl.NumPredictors elements correspond to the coefficients of the predictor variables ordered by the predictor data columns. The last element corresponds to the model variance.

If Width is a scalar, then simulate applies Width to all PriorMdl.NumPredictors + PriorMdl.Intercept + 1 marginal distributions.
If Width is a numeric vector, then simulate applies the first element to the intercept (if one exists), the next PriorMdl.NumPredictors elements to the regression coefficients corresponding to the predictor variables in X, and the last element to the disturbance variance.
If the sample size (size(X,1)) is less than 100, then Width is 10 by default.
If the sample size is at least 100, then simulate sets Width to the vector of corresponding posterior standard deviations by default, assuming a diffuse prior model (diffuseblm).

The typical width of the slice sampler does not affect convergence of the MCMC sample. It does affect the number of required function evaluations, that is, the efficiency of the algorithm. If the width is too small, then the algorithm can implement an excessive number of function evaluations to determine the appropriate sampling width. If the width is too large, then the algorithm might have to decrease the width to an appropriate size, which requires function evaluations.

simulate sends Width to the slicesample function. For more details, see slicesample.

Tip

For maximum flexibility, specify the slice sampler width width by using the 'Options' name-value pair argument. For example:
```
'Options',sampleroptions('Sampler',"slice",'Width',width)
```

Example: 'Width',[100*ones(3,1);10]

Output Arguments

collapse all

`BetaSim` — Simulated regression coefficients
numeric matrix

Simulated regression coefficients, returned as an (Mdl.Intercept + Mdl.NumPredictors)-by-NumDraws numeric matrix. Rows correspond to the variables in Mdl.VarNames, and columns correspond to individual, successive, independent draws from the distribution.

`sigma2Sim` — Simulated disturbance variance
numeric vector of positive values

Simulated disturbance variance, returned as a 1-by-NumDraws numeric vector of positive values. Columns correspond to individual, successive, independent draws from the distribution.

`RegimeSim` — Simulated regimes
logical matrix

Simulated regimes indicating variable inclusion or exclusion from the model, returned as an (Mdl.Intercept + Mdl.NumPredictors)-by-NumDraws logical matrix. Rows correspond to the variables in Mdl.VarNames, and columns correspond to individual, successive, independent draws from the distribution.

simulate returns Regime only if Mdl is a mixconjugateblm or mixsemiconjugateblm model object.

RegimeSim(k,d) = true indicates the inclusion of the variable Mdl.VarNames(k) in the model of draw d, and RegimeSim(k,d) = false indicates the exclusion of that variable in the model of draw d.

Limitations

simulate cannot draw values from an improper distribution, that is, a distribution whose density does not integrate to 1.
If Mdl is an empiricalblm model object, then you cannot specify Beta or Sigma2. You cannot simulate from the conditional posterior distributions by using an empirical distribution.

More About

collapse all

Bayesian Linear Regression Model

A Bayesian linear regression model treats the parameters β and σ² in the multiple linear regression (MLR) model y_t = x_tβ + ε_t as random variables.

For times t = 1,...,T:

y_t is the observed response.
x_t is a 1-by-(p + 1) row vector of observed values of p predictors. To accommodate a model intercept, x_1t = 1 for all t.
β is a (p + 1)-by-1 column vector of regression coefficients corresponding to the variables that compose the columns of x_t.
ε_t is the random disturbance with a mean of zero and Cov(ε) = σ²I_T×T, while ε is a T-by-1 vector containing all disturbances. These assumptions imply that the data likelihood is

$ℓ (β, σ^{2} | y, x) = \prod_{t = 1}^{T} ϕ (y_{t}; x_{t} β, σ^{2}) .$
ϕ(y_t;x_tβ,σ²) is the Gaussian probability density with mean x_tβ and variance σ² evaluated at y_t;.

Before considering the data, you impose a joint prior distribution assumption on (β,σ²). In a Bayesian analysis, you update the distribution of the parameters by using information about the parameters obtained from the likelihood of the data. The result is the joint posterior distribution of (β,σ²) or the conditional posterior distributions of the parameters.

Algorithms

Whenever simulate must estimate a posterior distribution (for example, when Mdl represents a prior distribution and you supply X and y) and the posterior is analytically tractable, simulate simulates directly from the posterior. Otherwise, simulate resorts to Monte Carlo simulation to estimate the posterior. For more details, see Posterior Estimation and Inference.
If Mdl is a joint posterior model, then simulate simulates data from it differently compared to when Mdl is a joint prior model and you supply X and y. Therefore, if you set the same random seed and generate random values both ways, then you might not obtain the same values. However, corresponding empirical distributions based on a sufficient number of draws is effectively equivalent.
This figure shows how simulate reduces the sample by using the values of NumDraws, Thin, and BurnIn.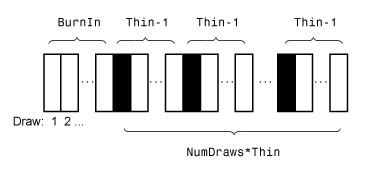

Rectangles represent successive draws from the distribution. simulate removes the white rectangles from the sample. The remaining NumDraws black rectangles compose the sample.
If Mdl is a semiconjugateblm model object, then simulate samples from the posterior distribution by applying the Gibbs sampler.
1. simulate uses the default value of Sigma2Start for σ² and draws a value of β from π(β|σ²,X,y).
2. simulate draws a value of σ² from π(σ²|β,X,y) by using the previously generated value of β.
3. The function repeats steps 1 and 2 until convergence. To assess convergence, draw a trace plot of the sample.
If you specify BetaStart, then simulate draws a value of σ² from π(σ²|β,X,y) to start the Gibbs sampler. simulate does not return this generated value of σ².
If Mdl is an empiricalblm model object and you do not supply X and y, then simulate draws from Mdl.BetaDraws and Mdl.Sigma2Draws. If NumDraws is less than or equal to numel(Mdl.Sigma2Draws), then simulate returns the first NumDraws elements of Mdl.BetaDraws and Mdl.Sigma2Draws as random draws for the corresponding parameter. Otherwise, simulate randomly resamples NumDraws elements from Mdl.BetaDraws and Mdl.Sigma2Draws.
If Mdl is a customblm model object, then simulate uses an MCMC sampler to draw from the posterior distribution. At each iteration, the software concatenates the current values of the regression coefficients and disturbance variance into an (Mdl.Intercept + Mdl.NumPredictors + 1)-by-1 vector, and passes it to Mdl.LogPDF. The value of the disturbance variance is the last element of this vector.
The HMC sampler requires both the log density and its gradient. The gradient should be a (NumPredictors+Intercept+1)-by-1 vector. If the derivatives of certain parameters are difficult to compute, then, in the corresponding locations of the gradient, supply NaN values instead. simulate replaces NaN values with numerical derivatives.
If Mdl is a lassoblm, mixconjugateblm, or mixsemiconjugateblm model object and you supply X and y, then simulate samples from the posterior distribution by applying the Gibbs sampler. If you do not supply the data, then simulate samples from the analytical, unconditional prior distributions.
simulate does not return default starting values that it generates.
If Mdl is a mixconjugateblm or mixsemiconjugateblm, then simulate draws from the regime distribution first, given the current state of the chain (the values of RegimeStart, BetaStart, and Sigma2Start). If you draw one sample and do not specify values for RegimeStart, BetaStart, and Sigma2Start, then simulate uses the default values and issues a warning.

Version History

Introduced in R2017a

simulate

Syntax

Description

Examples

Simulate Parameter Value from Prior and Posterior Distributions

Implement Gibbs Sampler for Posterior Estimation

Simulate Regimes from SSVS Predictor Selection

Robust Regression Using Gibbs Sampler

Estimate Maximum A Posteriori Probability Using Monte Carlo

Input Arguments

`Mdl` — Bayesian linear regression model
`conjugateblm` model object | `semiconjugateblm` model object | `diffuseblm` model object | `mixconjugateblm` model object | `lassoblm` model object

`X` — Predictor data
numeric matrix

`y` — Response data
numeric vector

Name-Value Arguments

`NumDraws` — Effective number of draws
`1` (default) | positive integer

`Beta` — Value of regression coefficients for simulation from conditional distribution of disturbance variance
empty array (`[]`) (default) | numeric column vector

`Sigma2` — Value of disturbance variance for simulation from conditional distribution of regression coefficients
empty array (`[]`) (default) | positive numeric scalar

`BurnIn` — Number of draws to remove from beginning of sample
`0` (default) | nonnegative scalar

`Thin` — Adjusted sample size multiplier
`1` (default) | positive integer

`BetaStart` — Starting values of regression coefficients for sampler
numeric column vector

`Sigma2Start` — Starting values of disturbance variance for sampler
positive numeric scalar

`RegimeStart` — Starting values of latent regimes for sampler
`true(Mdl.Intercept + Mdl.NumPredictors)` (default) | logical column vector

`Reparameterize` — Reparameterization of σ² as log(σ²)
`false` (default) | `true`

`Sampler` — MCMC sampler
`'slice'` (default) | `'metropolis'` | `'hmc'`

`Options` — Sampler options
`[]` (default) | structure array

`Width` — Typical sampling-interval width
positive numeric scalar | numeric vector of positive values

Output Arguments

`BetaSim` — Simulated regression coefficients
numeric matrix

`sigma2Sim` — Simulated disturbance variance
numeric vector of positive values

`RegimeSim` — Simulated regimes
logical matrix

Limitations

More About

Bayesian Linear Regression Model

Algorithms

Version History

See Also

Objects

Functions

Topics

simulate

Syntax

Description

Examples

Simulate Parameter Value from Prior and Posterior Distributions

Implement Gibbs Sampler for Posterior Estimation

Simulate Regimes from SSVS Predictor Selection

Robust Regression Using Gibbs Sampler

Estimate Maximum A Posteriori Probability Using Monte Carlo

Input Arguments

Mdl — Bayesian linear regression model conjugateblm model object | semiconjugateblm model object | diffuseblm model object | mixconjugateblm model object | lassoblm model object

X — Predictor data numeric matrix

y — Response data numeric vector

Name-Value Arguments

NumDraws — Effective number of draws 1 (default) | positive integer

Beta — Value of regression coefficients for simulation from conditional distribution of disturbance variance empty array ([]) (default) | numeric column vector

Sigma2 — Value of disturbance variance for simulation from conditional distribution of regression coefficients empty array ([]) (default) | positive numeric scalar

BurnIn — Number of draws to remove from beginning of sample 0 (default) | nonnegative scalar

Thin — Adjusted sample size multiplier 1 (default) | positive integer

BetaStart — Starting values of regression coefficients for sampler numeric column vector

Sigma2Start — Starting values of disturbance variance for sampler positive numeric scalar

RegimeStart — Starting values of latent regimes for sampler true(Mdl.Intercept + Mdl.NumPredictors) (default) | logical column vector

Reparameterize — Reparameterization of σ2 as log(σ2) false (default) | true

Sampler — MCMC sampler 'slice' (default) | 'metropolis' | 'hmc'

Options — Sampler options [] (default) | structure array

Width — Typical sampling-interval width positive numeric scalar | numeric vector of positive values

Output Arguments

BetaSim — Simulated regression coefficients numeric matrix

sigma2Sim — Simulated disturbance variance numeric vector of positive values

RegimeSim — Simulated regimes logical matrix

Limitations

More About

Bayesian Linear Regression Model

Algorithms

Version History

See Also

Objects

Functions

Topics

`Mdl` — Bayesian linear regression model
`conjugateblm` model object | `semiconjugateblm` model object | `diffuseblm` model object | `mixconjugateblm` model object | `lassoblm` model object

`X` — Predictor data
numeric matrix

`y` — Response data
numeric vector

`NumDraws` — Effective number of draws
`1` (default) | positive integer

`Beta` — Value of regression coefficients for simulation from conditional distribution of disturbance variance
empty array (`[]`) (default) | numeric column vector

`Sigma2` — Value of disturbance variance for simulation from conditional distribution of regression coefficients
empty array (`[]`) (default) | positive numeric scalar

`BurnIn` — Number of draws to remove from beginning of sample
`0` (default) | nonnegative scalar

`Thin` — Adjusted sample size multiplier
`1` (default) | positive integer

`BetaStart` — Starting values of regression coefficients for sampler
numeric column vector

`Sigma2Start` — Starting values of disturbance variance for sampler
positive numeric scalar

`RegimeStart` — Starting values of latent regimes for sampler
`true(Mdl.Intercept + Mdl.NumPredictors)` (default) | logical column vector

`Reparameterize` — Reparameterization of σ² as log(σ²)
`false` (default) | `true`

`Sampler` — MCMC sampler
`'slice'` (default) | `'metropolis'` | `'hmc'`

`Options` — Sampler options
`[]` (default) | structure array

`Width` — Typical sampling-interval width
positive numeric scalar | numeric vector of positive values

`BetaSim` — Simulated regression coefficients
numeric matrix

`sigma2Sim` — Simulated disturbance variance
numeric vector of positive values

`RegimeSim` — Simulated regimes
logical matrix