estimate
Estimate posterior distribution of Bayesian linear regression model parameters
Syntax
Description
To perform predictor variable selection for a Bayesian linear regression model, see estimate.
PosteriorMdl = estimate(PriorMdl,X,y)PosteriorMdl that characterizes the joint posterior distributions of the coefficients β and the disturbance variance σ2. PriorMdl specifies the joint prior distribution of the parameters and the structure of the linear regression model. X is the predictor data and y is the response data. PriorMdl and PosteriorMdl might not be the same object type.
To produce PosteriorMdl, the estimate function updates the prior distribution with information about the parameters that it obtains from the data.
NaNs in the data indicate missing values, which estimate removes by using list-wise deletion.
PosteriorMdl = estimate(PriorMdl,X,y,Name,Value)
If you specify the Beta or Sigma2 name-value pair argument, then PosteriorMdl and PriorMdl are equal.
[ uses any of the input argument combinations in the previous syntaxes to return a table that contains the following for each parameter: the posterior mean and standard deviation, 95% credible interval, posterior probability that the parameter is greater than 0, and description of the posterior distribution (if one exists). Also, the table contains the posterior covariance matrix of β and σ2. If you specify the PosteriorMdl,Summary]
= estimate(___)Beta or Sigma2 name-value pair argument, then estimate returns conditional posterior estimates.
Examples
Consider a model that predicts the fuel economy (in MPG) of a car given its engine displacement and weight.
Load the carsmall data set.
load carsmall
x = [Displacement Weight];
y = MPG;Regress fuel economy onto engine displacement and weight, including an intercept to obtain ordinary least-squares (OLS) estimates.
Mdl = fitlm(x,y)
Mdl =
Linear regression model:
y ~ 1 + x1 + x2
Estimated Coefficients:
Estimate SE tStat pValue
__________ _________ _______ __________
(Intercept) 46.925 2.0858 22.497 6.0509e-39
x1 -0.014593 0.0082695 -1.7647 0.080968
x2 -0.0068422 0.0011337 -6.0353 3.3838e-08
Number of observations: 94, Error degrees of freedom: 91
Root Mean Squared Error: 4.09
R-squared: 0.747, Adjusted R-Squared: 0.741
F-statistic vs. constant model: 134, p-value = 7.22e-28
Mdl.MSE
ans = 16.7100
Create a default, diffuse prior distribution for one predictor.
p = 2; PriorMdl = bayeslm(p);
PriorMdl is a diffuseblm model object.
Use default options to estimate the posterior distribution.
PosteriorMdl = estimate(PriorMdl,x,y);
Method: Analytic posterior distributions
Number of observations: 94
Number of predictors: 3
| Mean Std CI95 Positive Distribution
--------------------------------------------------------------------------------
Intercept | 46.9247 2.1091 [42.782, 51.068] 1.000 t (46.92, 2.09^2, 91)
Beta(1) | -0.0146 0.0084 [-0.031, 0.002] 0.040 t (-0.01, 0.01^2, 91)
Beta(2) | -0.0068 0.0011 [-0.009, -0.005] 0.000 t (-0.01, 0.00^2, 91)
Sigma2 | 17.0855 2.5905 [12.748, 22.866] 1.000 IG(45.50, 0.0013)
PosteriorMdl is a conjugateblm model object.
The posterior means and the OLS coefficient estimates are almost identical. Also, the posterior standard deviations and OLS standard errors are almost identical. The posterior mean of Sigma2 is close to the OLS mean squared error (MSE).
Consider the multiple linear regression model that predicts the US real gross national product (GNPR) using a linear combination of total employment (E) and real wages (WR).

For all  ,
, 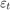 is a series of independent Gaussian disturbances with a mean of 0 and variance
is a series of independent Gaussian disturbances with a mean of 0 and variance  . Assume these prior distributions:
. Assume these prior distributions:
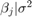 is a 3-D t distribution with 10 degrees of freedom for each component, correlation matrix
is a 3-D t distribution with 10 degrees of freedom for each component, correlation matrix C, locationct, and scalest.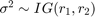 , with shape
, with shape  and scale
and scale  .
.
bayeslm treats these assumptions and the data likelihood as if the corresponding posterior is analytically intractable.
Declare a MATLAB® function that:
Accepts values of
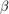 and
and  together in a column vector, and accepts values of the hyperparameters
together in a column vector, and accepts values of the hyperparametersReturns the value of the joint prior distribution,
 , given the values of
, given the values of 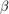 and
and 
function logPDF = priorMVTIG(params,ct,st,dof,C,a,b) %priorMVTIG Log density of multivariate t times inverse gamma % priorMVTIG passes params(1:end-1) to the multivariate t density % function with dof degrees of freedom for each component and positive % definite correlation matrix C. priorMVTIG returns the log of the product of % the two evaluated densities. % % params: Parameter values at which the densities are evaluated, an % m-by-1 numeric vector. % % ct: Multivariate t distribution component centers, an (m-1)-by-1 % numeric vector. Elements correspond to the first m-1 elements % of params. % % st: Multivariate t distribution component scales, an (m-1)-by-1 % numeric (m-1)-by-1 numeric vector. Elements correspond to the % first m-1 elements of params. % % dof: Degrees of freedom for the multivariate t distribution, a % numeric scalar or (m-1)-by-1 numeric vector. priorMVTIG expands % scalars such that dof = dof*ones(m-1,1). Elements of dof % correspond to the elements of params(1:end-1). % % C: Correlation matrix for the multivariate t distribution, an % (m-1)-by-(m-1) symmetric, positive definite matrix. Rows and % columns correspond to the elements of params(1:end-1). % % a: Inverse gamma shape parameter, a positive numeric scalar. % % b: Inverse gamma scale parameter, a positive scalar. % beta = params(1:(end-1)); sigma2 = params(end); tVal = (beta - ct)./st; mvtDensity = mvtpdf(tVal,C,dof); igDensity = sigma2^(-a-1)*exp(-1/(sigma2*b))/(gamma(a)*b^a); logPDF = log(mvtDensity*igDensity); end
Create an anonymous function that operates like priorMVTIG, but accepts the parameter values only, and holds the hyperparameter values fixed at arbitrarily chosen values.
prednames = ["E" "WR"]; p = numel(prednames); numcoeff = p + 1; rng(1); % For reproducibility dof = 10; V = rand(numcoeff); Sigma = 0.5*(V + V') + numcoeff*eye(numcoeff); st = sqrt(diag(Sigma)); C = diag(1./st)*Sigma*diag(1./st); ct = rand(numcoeff,1); a = 10*rand; b = 10*rand; logPDF = @(params)priorMVTIG(params,ct,st,dof,C,a,b);
Create a custom joint prior model for the linear regression parameters. Specify the number of predictors p. Also, specify the function handle for priorMVTIG and the variable names.
PriorMdl = bayeslm(p,'ModelType','custom','LogPDF',logPDF,... 'VarNames',prednames);
PriorMdl is a customblm Bayesian linear regression model object representing the prior distribution of the regression coefficients and disturbance variance.
Load the Nelson-Plosser data set. Create variables for the response and predictor series.
load Data_NelsonPlosser X = DataTable{:,PriorMdl.VarNames(2:end)}; y = DataTable{:,"GNPR"};
Estimate the marginal posterior distributions of 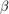 and
and  using the Hamiltonian Monte Carlo (HMC) sampler. Specify drawing 10,000 samples and a burn-in period of 1000 draws.
using the Hamiltonian Monte Carlo (HMC) sampler. Specify drawing 10,000 samples and a burn-in period of 1000 draws.
PosteriorMdl = estimate(PriorMdl,X,y,'Sampler','hmc','NumDraws',1e4,... 'Burnin',1e3);
Method: MCMC sampling with 10000 draws
Number of observations: 62
Number of predictors: 3
| Mean Std CI95 Positive Distribution
------------------------------------------------------------------------------
Intercept | -3.6417 5.6972 [-16.242, 6.365] 0.247 Empirical
E | -0.0056 0.0006 [-0.007, -0.004] 0.000 Empirical
WR | 15.2467 0.7734 [13.735, 16.721] 1.000 Empirical
Sigma2 | 1285.3591 241.2001 [903.847, 1832.438] 1.000 Empirical
PosteriorMdl is an empiricalblm model object storing the draws from the posterior distributions.
View a trace plot and an ACF plot of the draws from the posterior of 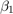 (for example) and the disturbance variance. Do not plot the burn-in period.
(for example) and the disturbance variance. Do not plot the burn-in period.
figure; subplot(2,1,1) plot(PosteriorMdl.BetaDraws(2,1001:end)); title(['Trace Plot ' char(8212) ' \beta_1']); xlabel('MCMC Draw') ylabel('Simulation Index') subplot(2,1,2) autocorr(PosteriorMdl.BetaDraws(2,1001:end)) figure; subplot(2,1,1) plot(PosteriorMdl.Sigma2Draws(1001:end)); title(['Trace Plot ' char(8212) ' Disturbance Variance']); xlabel('MCMC Draw') ylabel('Simulation Index') subplot(2,1,2) autocorr(PosteriorMdl.Sigma2Draws(1001:end))


The MCMC sample of the disturbance variance appears to mix well.
Consider the regression model in Estimate Posterior Using Hamiltonian Monte Carlo Sampler. This example uses the same data and context, but assumes a diffuse prior model instead.
Create a diffuse prior model for the linear regression parameters. Specify the number of predictors p and the names of the regression coefficients.
p = 3; PriorMdl = bayeslm(p,'ModelType','diffuse','VarNames',["IPI" "E" "WR"])
PriorMdl =
diffuseblm with properties:
NumPredictors: 3
Intercept: 1
VarNames: {4×1 cell}
| Mean Std CI95 Positive Distribution
-----------------------------------------------------------------------------
Intercept | 0 Inf [ NaN, NaN] 0.500 Proportional to one
IPI | 0 Inf [ NaN, NaN] 0.500 Proportional to one
E | 0 Inf [ NaN, NaN] 0.500 Proportional to one
WR | 0 Inf [ NaN, NaN] 0.500 Proportional to one
Sigma2 | Inf Inf [ NaN, NaN] 1.000 Proportional to 1/Sigma2
PriorMdl is a diffuseblm model object.
Load the Nelson-Plosser data set. Create variables for the response and predictor series.
load Data_NelsonPlosser X = DataTable{:,PriorMdl.VarNames(2:end)}; y = DataTable{:,'GNPR'};
Estimate the conditional posterior distribution of given the data and that , and return the estimation summary table to access the estimates.
[Mdl,SummaryBeta] = estimate(PriorMdl,X,y,'Sigma2',2);Method: Analytic posterior distributions
Conditional variable: Sigma2 fixed at 2
Number of observations: 62
Number of predictors: 4
| Mean Std CI95 Positive Distribution
--------------------------------------------------------------------------------
Intercept | -24.2536 1.8696 [-27.918, -20.589] 0.000 N (-24.25, 1.87^2)
IPI | 4.3913 0.0301 [ 4.332, 4.450] 1.000 N (4.39, 0.03^2)
E | 0.0011 0.0001 [ 0.001, 0.001] 1.000 N (0.00, 0.00^2)
WR | 2.4682 0.0743 [ 2.323, 2.614] 1.000 N (2.47, 0.07^2)
Sigma2 | 2 0 [ 2.000, 2.000] 1.000 Fixed value
estimate displays a summary of the conditional posterior distribution of . Because is fixed at 2 during estimation, inferences on it are trivial.
Extract the mean vector and covariance matrix of the conditional posterior of from the estimation summary table.
condPostMeanBeta = SummaryBeta.Mean(1:(end - 1))
condPostMeanBeta = 4×1
-24.2536
4.3913
0.0011
2.4682
CondPostCovBeta = SummaryBeta.Covariances(1:(end - 1),1:(end - 1))
CondPostCovBeta = 4×4
3.4956 0.0350 -0.0001 0.0241
0.0350 0.0009 -0.0000 -0.0013
-0.0001 -0.0000 0.0000 -0.0000
0.0241 -0.0013 -0.0000 0.0055
Display Mdl.
Mdl
Mdl =
diffuseblm with properties:
NumPredictors: 3
Intercept: 1
VarNames: {4×1 cell}
| Mean Std CI95 Positive Distribution
-----------------------------------------------------------------------------
Intercept | 0 Inf [ NaN, NaN] 0.500 Proportional to one
IPI | 0 Inf [ NaN, NaN] 0.500 Proportional to one
E | 0 Inf [ NaN, NaN] 0.500 Proportional to one
WR | 0 Inf [ NaN, NaN] 0.500 Proportional to one
Sigma2 | Inf Inf [ NaN, NaN] 1.000 Proportional to 1/Sigma2
Because estimate computes the conditional posterior distribution, it returns the original prior model, not the posterior, in the first position of the output argument list.
Estimate the conditional posterior distributions of given that is condPostMeanBeta.
[~,SummarySigma2] = estimate(PriorMdl,X,y,'Beta',condPostMeanBeta);Method: Analytic posterior distributions
Conditional variable: Beta fixed at -24.2536 4.3913 0.00112035 2.46823
Number of observations: 62
Number of predictors: 4
| Mean Std CI95 Positive Distribution
--------------------------------------------------------------------------------
Intercept | -24.2536 0 [-24.254, -24.254] 0.000 Fixed value
IPI | 4.3913 0 [ 4.391, 4.391] 1.000 Fixed value
E | 0.0011 0 [ 0.001, 0.001] 1.000 Fixed value
WR | 2.4682 0 [ 2.468, 2.468] 1.000 Fixed value
Sigma2 | 48.5138 9.0088 [33.984, 69.098] 1.000 IG(31.00, 0.00069)
estimate displays a summary of the conditional posterior distribution of . Because is fixed to condPostMeanBeta during estimation, inferences on it are trivial.
Extract the mean and variance of the conditional posterior of from the estimation summary table.
condPostMeanSigma2 = SummarySigma2.Mean(end)
condPostMeanSigma2 = 48.5138
CondPostVarSigma2 = SummarySigma2.Covariances(end,end)
CondPostVarSigma2 = 81.1581
Consider the regression model in Estimate Posterior Using Hamiltonian Monte Carlo Sampler. This example uses the same data and context, but assumes a semiconjugate prior model instead.
Create a semiconjugate prior model for the linear regression parameters. Specify the number of predictors p and the names of the regression coefficients.
p = 3; PriorMdl = bayeslm(p,'ModelType','semiconjugate',... 'VarNames',["IPI" "E" "WR"]);
PriorMdl is a semiconjugateblm model object.
Load the Nelson-Plosser data set. Create variables for the response and predictor series.
load Data_NelsonPlosser X = DataTable{:,PriorMdl.VarNames(2:end)}; y = DataTable{:,'GNPR'};
Estimate the marginal posterior distributions of and .
rng(1); % For reproducibility
[PosteriorMdl,Summary] = estimate(PriorMdl,X,y);Method: Gibbs sampling with 10000 draws
Number of observations: 62
Number of predictors: 4
| Mean Std CI95 Positive Distribution
-------------------------------------------------------------------------
Intercept | -23.9922 9.0520 [-41.734, -6.198] 0.005 Empirical
IPI | 4.3929 0.1458 [ 4.101, 4.678] 1.000 Empirical
E | 0.0011 0.0003 [ 0.000, 0.002] 0.999 Empirical
WR | 2.4711 0.3576 [ 1.762, 3.178] 1.000 Empirical
Sigma2 | 46.7474 8.4550 [33.099, 66.126] 1.000 Empirical
PosteriorMdl is an empiricalblm model object because marginal posterior distributions of semiconjugate models are analytically intractable, so estimate must implement a Gibbs sampler. Summary is a table containing the estimates and inferences that estimate displays at the command line.
Display the summary table.
Summary
Summary=5×6 table
Mean Std CI95 Positive Distribution Covariances
_________ __________ ________________________ ________ _____________ ______________________________________________________________________
Intercept -23.992 9.052 -41.734 -6.1976 0.0053 {'Empirical'} 81.938 0.81622 -0.0025308 0.58928 0
IPI 4.3929 0.14578 4.1011 4.6782 1 {'Empirical'} 0.81622 0.021252 -7.1663e-06 -0.030939 0
E 0.0011124 0.00033976 0.00045128 0.0017883 0.9989 {'Empirical'} -0.0025308 -7.1663e-06 1.1544e-07 -8.4598e-05 0
WR 2.4711 0.3576 1.7622 3.1781 1 {'Empirical'} 0.58928 -0.030939 -8.4598e-05 0.12788 0
Sigma2 46.747 8.455 33.099 66.126 1 {'Empirical'} 0 0 0 0 71.487
Access the 95% equitailed credible interval of the regression coefficient of IPI.
Summary.CI95(2,:)
ans = 1×2
4.1011 4.6782
Input Arguments
Bayesian linear regression model representing a prior model, specified as an object in this table.
| Model Object | Description |
|---|---|
conjugateblm | Dependent, normal-inverse-gamma conjugate model returned by bayeslm or estimate |
semiconjugateblm | Independent, normal-inverse-gamma semiconjugate model returned by bayeslm |
diffuseblm | Diffuse prior model returned by bayeslm |
empiricalblm | Prior model characterized by samples from prior distributions, returned by bayeslm or estimate |
customblm | Prior distribution function that you declare returned by bayeslm |
PriorMdl can also represent a joint posterior model returned by estimate, either a conjugateblm or empiricalblm model object. In this case, estimate updates the joint posterior distribution using the new observations in X and y.
Predictor data for the multiple linear regression model, specified as
a numObservations-by-PriorMdl.NumPredictors numeric
matrix. numObservations is the number of observations and must be
equal to the length of y.
Data Types: double
Response data for the multiple linear regression model, specified
as a numeric vector with numObservations elements.
Data Types: double
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: 'Sigma2',2 specifies estimating the conditional posterior distribution of the regression coefficients given the data and that the specified disturbance variance is 2.
Options for All Prior Distributions
Flag to display Bayesian estimator summary at the command line, specified as the comma-separated pair consisting of 'Display' and a value in this table.
| Value | Description |
|---|---|
true | estimate prints estimation information and a table summarizing the Bayesian estimators to the command line. |
false | estimate does not print to the command line. |
The estimation information includes the estimation method, fixed parameters, the number of observations, and the number of predictors. The summary table contains estimated posterior means and standard deviations (square root of the posterior variance), 95% equitailed credible intervals, the posterior probability that the parameter is greater than 0, and a description of the posterior distribution (if known).
If you specify one of Beta or Sigma2, then estimate includes your specification in the display, and corresponding posterior estimates are trivial.
Example: 'Display',false
Data Types: logical
Options for All Prior Distributions Except Empirical
Value of the regression coefficients for conditional posterior distribution estimation of the
disturbance variance, specified as the comma-separated pair consisting of
'Beta' and a (PriorMdl.Intercept +
PriorMdl.NumPredictors)-by-1 numeric vector.
estimate estimates the characteristics of
π(σ2|y,X,β
= Beta), where y is
y, X is X, and
Beta is the value of 'Beta'. If
PriorMdl.Intercept is true, then
Beta(1) corresponds to the model intercept. All other values
correspond to the predictor variables that compose the columns of
X. Beta cannot contain any
NaN values (that is, all coefficients must be known).
You cannot specify Beta and Sigma2 simultaneously.
By default, estimate does not compute characteristics of the conditional posterior of σ2.
Example: 'Beta',1:3
Data Types: double
Value of the disturbance variance for conditional posterior distribution estimation of the
regression coefficients, specified as the comma-separated pair
consisting of 'Sigma2' and a positive numeric
scalar. estimate estimates
characteristics of
π(β|y,X,Sigma2),
where y is y,
X is
X, and
Sigma2 is the value of
'Sigma2'.
You cannot specify Sigma2 and Beta
simultaneously.
By default, estimate does not compute characteristics of the conditional posterior of β.
Example: 'Sigma2',1
Data Types: double
Options for Semiconjugate, Empirical, and Custom Prior Distributions
Monte Carlo simulation adjusted sample size, specified as the comma-separated pair consisting of 'NumDraws' and a positive integer. estimate actually draws BurnIn + NumDraws*Thin samples, but it bases the estimates off NumDraws samples. For details on how estimate reduces the full Monte Carlo sample, see Algorithms.
If PriorMdl is a semiconjugateblm model and you specify Beta or Sigma2, then MATLAB® ignores NumDraws.
Example: 'NumDraws',1e7
Data Types: double
Options for Semiconjugate and Custom Prior Distributions
Number of draws to remove from the beginning of the Monte Carlo sample to reduce transient
effects, specified as the comma-separated pair consisting of 'BurnIn'
and a nonnegative scalar. For details on how estimate reduces
the full Monte Carlo sample, see Algorithms.
Tip
To help you specify the appropriate burn-in period size, determine the extent of the transient behavior in the Monte Carlo sample by specifying 'BurnIn',0, simulating a few thousand observations using simulate, and then plotting the paths.
Example: 'BurnIn',0
Data Types: double
Monte Carlo adjusted sample size multiplier, specified as the comma-separated pair consisting of 'Thin' and a positive integer.
The actual Monte Carlo sample size is BurnIn + NumDraws*Thin. After discarding the burn-in, estimate discards every Thin – 1 draws, and then retains the next. For details on how estimate reduces the full Monte Carlo sample, see Algorithms.
Tip
To reduce potential large serial correlation in the Monte Carlo sample, or to reduce the
memory consumption of the draws stored in PosteriorMdl, specify
a large value for Thin.
Example: 'Thin',5
Data Types: double
Starting values of the regression coefficients for the Markov chain Monte Carlo (MCMC)
sample, specified as the comma-separated pair consisting of
'BetaStart' and a numeric column vector with
(PriorMdl.Intercept + PriorMdl.NumPredictors)
elements. By default, BetaStart is the ordinary least-squares (OLS)
estimate.
Tip
A good practice is to run estimate multiple times using
different parameter starting values. Verify that the solutions from each run
converge to similar values.
Example: 'BetaStart',[1; 2; 3]
Data Types: double
Starting values of the disturbance variance for the MCMC sample, specified as the
comma-separated pair consisting of 'Sigma2Start' and a positive
numeric scalar. By default, Sigma2Start is the OLS residual mean
squared error.
Tip
A good practice is to run estimate multiple times using different
parameter starting values. Verify that the solutions from each run converge to
similar values.
Example: 'Sigma2Start',4
Data Types: double
Options for Custom Prior Distributions
Reparameterization of σ2 as
log(σ2) during posterior estimation
and simulation, specified as the comma-separated pair consisting of
'Reparameterize' and a value in this table.
| Value | Description |
|---|---|
false | estimate does not reparameterize
σ2. |
true | estimate reparameterizes
σ2 as
log(σ2).
estimate converts results back to the
original scale and does not change the functional form of
PriorMdl.LogPDF. |
Tip
If you experience numeric instabilities during the posterior estimation or
simulation of σ2, then specify
'Reparameterize',true.
Example: 'Reparameterize',true
Data Types: logical
MCMC sampler, specified as the comma-separated pair consisting of
'Sampler' and a value in this table.
| Value | Description |
|---|---|
'slice' | Slice sampler |
'metropolis' | Random walk Metropolis sampler |
'hmc' | Hamiltonian Monte Carlo (HMC) sampler |
Tip
To increase the quality of the MCMC draws, tune the sampler.
Before calling
estimate, specify the tuning parameters and their values by usingsampleroptions. For example, to specify the slice sampler widthwidth, use:options = sampleroptions('Sampler',"slice",'Width',width);
Specify the object containing the tuning parameter specifications returned by
sampleroptionsby using the'Options'name-value pair argument. For example, to use the tuning parameter specifications inoptions, specify:'Options',options
If you specify the HMC sampler, then a best practice is to provide the gradient for some variables, at least.
estimateresorts the numerical computation of any missing partial derivatives (NaNvalues) in the gradient vector.
Example: 'Sampler',"hmc"
Data Types: string
Sampler options, specified as the comma-separated pair consisting of
'Options' and a structure array returned by sampleroptions. Use 'Options' to specify the MCMC
sampler and its tuning-parameter values.
Example: 'Options',sampleroptions('Sampler',"hmc")
Data Types: struct
Typical sampling-interval width around the current value in the marginal distributions for the
slice sampler, specified as the comma-separated pair consisting of
'Width' and a positive numeric scalar or a
(PriorMdl.Intercept + PriorMdl.NumPredictors +
1)-by-1 numeric vector of positive values. The first element
corresponds to the model intercept, if one exists in the model. The next
PriorMdl.NumPredictors elements correspond to the coefficients of
the predictor variables ordered by the predictor data columns. The last element
corresponds to the model variance.
If
Widthis a scalar, thenestimateappliesWidthto allPriorMdl.NumPredictors+PriorMdl.Intercept+1marginal distributions.If
Widthis a numeric vector, thenestimateapplies the first element to the intercept (if one exists), the nextPriorMdl.NumPredictorselements to the regression coefficients corresponding to the predictor variables inX, and the last element to the disturbance variance.If the sample size (
size(X,1)) is less than 100, thenWidthis10by default.If the sample size is at least 100, then
estimatesetsWidthto the vector of corresponding posterior standard deviations by default, assuming a diffuse prior model (diffuseblm).
The typical width of the slice sampler does not affect convergence of the MCMC sample. It does affect the number of required function evaluations, that is, the efficiency of the algorithm. If the width is too small, then the algorithm can implement an excessive number of function evaluations to determine the appropriate sampling width. If the width is too large, then the algorithm might have to decrease the width to an appropriate size, which requires function evaluations.
estimate sends Width to the
slicesample function. For more details, see slicesample.
Tip
For maximum flexibility, specify the slice sampler width
widthby using the'Options'name-value pair argument. For example:'Options',sampleroptions('Sampler',"slice",'Width',width)
Example: 'Width',[100*ones(3,1);10]
Output Arguments
Bayesian linear regression model storing distribution characteristics, returned as a conjugateblm, semiconjugateblm, diffuseblm, empiricalblm, or customblm model object.
If you do not specify either
BetaorSigma2(their values are[]), thenestimateupdates the prior model using the data likelihood to form the posterior distribution.PosteriorMdlcharacterizes the posterior distribution. Its object type depends on the prior model type (PriorMdl).Model Object PriorMdlconjugateblmconjugateblmordiffuseblmempiricalblmsemiconjugateblm,empiricalblm, orcustomblmIf you specify either
BetaorSigma2, thenPosteriorMdlequalsPriorMdl(the two models are the same object storing the same property values).estimatedoes not update the prior model to form the posterior model. However,estBeta,EstBetaCov,estSigma2,estSigma2Var, andSummarystore conditional posterior estimates.
For more details on the display of PosteriorMdl, see Summary.
For details on supported posterior distributions that are analytically tractable, see Analytically Tractable Posteriors.
Summary of Bayesian estimators, returned as a table. Summary contains the same information as the display of the estimation summary (Display). Rows correspond to parameters, and columns correspond to these posterior characteristics for each parameter:
Mean– Posterior meanStd– Posterior standard deviationCI95– 95% equitailed credible intervalPositive– The posterior probability the parameter is greater than 0Distribution– Description of the marginal or conditional posterior distribution of the parameter, when knownCovariances– Estimated covariance matrix of the coefficients and disturbance variance
Row names are the names in PriorMdl.VarNames. The name of the last row is Sigma2.
Alternatively, pass PosteriorMdl to summarize to obtain a summary of Bayesian estimators.
Limitations
If PriorMdl is an empiricalblm model object. You cannot specify Beta or Sigma2. You cannot estimate conditional posterior distributions by using an empirical prior distribution.
More About
A Bayesian linear regression model treats the parameters β and σ2 in the multiple linear regression (MLR) model yt = xtβ + εt as random variables.
For times t = 1,...,T:
yt is the observed response.
xt is a 1-by-(p + 1) row vector of observed values of p predictors. To accommodate a model intercept, x1t = 1 for all t.
β is a (p + 1)-by-1 column vector of regression coefficients corresponding to the variables that compose the columns of xt.
εt is the random disturbance with a mean of zero and Cov(ε) = σ2IT×T, while ε is a T-by-1 vector containing all disturbances. These assumptions imply that the data likelihood is
ϕ(yt;xtβ,σ2) is the Gaussian probability density with mean xtβ and variance σ2 evaluated at yt;.
Before considering the data, you impose a joint prior distribution assumption on (β,σ2). In a Bayesian analysis, you update the distribution of the parameters by using information about the parameters obtained from the likelihood of the data. The result is the joint posterior distribution of (β,σ2) or the conditional posterior distributions of the parameters.
Tips
Monte Carlo simulation is subject to variation. If
estimateuses Monte Carlo simulation, then estimates and inferences might vary when you callestimatemultiple times under seemingly equivalent conditions. To reproduce estimation results, set a random number seed by usingrngbefore callingestimate.If
estimateissues an error while estimating the posterior distribution using a custom prior model, then try adjusting initial parameter values by usingBetaStartorSigma2Start, or try adjusting the declared log prior function, and then reconstructing the model. The error might indicate that the log of the prior distribution is–Infat the specified initial values.
Algorithms
Whenever the prior distribution (
PriorMdl) and the data likelihood yield an analytically tractable posterior distribution,estimateevaluates the closed-form solutions to Bayes estimators. Otherwise,estimateresorts to Monte Carlo simulation to estimate parameters and draw inferences. For more details, see Posterior Estimation and Inference.This figure illustrates how
estimatereduces the Monte Carlo sample using the values ofNumDraws,Thin, andBurnIn. Rectangles represent successive draws from the distribution.estimateremoves the white rectangles from the Monte Carlo sample. The remainingNumDrawsblack rectangles compose the Monte Carlo sample.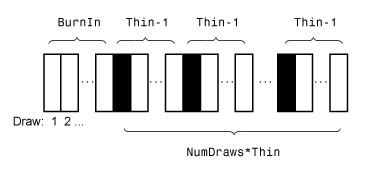
Version History
Introduced in R2017aFor a simpler interface, estimate returns only an estimated model and an estimation summary table. Now, the supported syntaxes are:
PosteriorMdl = estimate(...); [PosteriorMdl,Summary] = estimate(...);
In past releases, estimate returned these output arguments:
[PosteriorMdl,estBeta,EstBetaCov,estSigma2,estSigma2Var,Summary] = estimate(...);
estBeta, EstBetaCov, estSigma2, and estSigma2Var are posterior means and covariances of β and σ2.Starting in R2019b, if you request any output argument in a position greater than the second position, estimate issues this error:
Too many output arguments.
See Also
Objects
Functions
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
选择网站
选择网站以获取翻译的可用内容,以及查看当地活动和优惠。根据您的位置,我们建议您选择:。
您也可以从以下列表中选择网站:
如何获得最佳网站性能
选择中国网站(中文或英文)以获得最佳网站性能。其他 MathWorks 国家/地区网站并未针对您所在位置的访问进行优化。
美洲
- América Latina (Español)
- Canada (English)
- United States (English)
欧洲
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)