Create Moving Average Models
These examples show how to create various moving average (MA) models
by using the arima function.
Default MA Model
This example shows how to use the shorthand arima(p,D,q) syntax to specify the default MA
By default, all parameters in the created model object have unknown values, and the innovation distribution is Gaussian with constant variance.
Specify the default MA(3) model:
Mdl = arima(0,0,3)
Mdl =
arima with properties:
Description: "ARIMA(0,0,3) Model (Gaussian Distribution)"
SeriesName: "Y"
Distribution: Name = "Gaussian"
P: 0
D: 0
Q: 3
Constant: NaN
AR: {}
SAR: {}
MA: {NaN NaN NaN} at lags [1 2 3]
SMA: {}
Seasonality: 0
Beta: [1×0]
Variance: NaN
The output shows that the created model object, Mdl, has NaN values for all model parameters: the constant term, the MA coefficients, and the variance. You can modify the created model object using dot notation, or input it (along with data) to estimate.
MA Model with No Constant Term
This example shows how to specify an MA(q) model with constant term equal to zero. Use name-value syntax to specify a model that differs from the default model.
Specify an MA(2) model with no constant term,
where the innovation distribution is Gaussian with constant variance.
Mdl = arima('MALags',1:2,'Constant',0)
Mdl =
arima with properties:
Description: "ARIMA(0,0,2) Model (Gaussian Distribution)"
SeriesName: "Y"
Distribution: Name = "Gaussian"
P: 0
D: 0
Q: 2
Constant: 0
AR: {}
SAR: {}
MA: {NaN NaN} at lags [1 2]
SMA: {}
Seasonality: 0
Beta: [1×0]
Variance: NaN
The MALags name-value argument specifies the lags corresponding to nonzero MA coefficients. The property Constant in the created model object is equal to 0, as specified. The model object has default values for all other properties, including NaN values as placeholders for the unknown parameters: the MA coefficients and scalar variance.
You can modify the created model variable, or input it (along with data) to estimate.
MA Model with Nonconsecutive Lags
This example shows how to specify an MA(q) model with nonzero coefficients at nonconsecutive lags.
Specify an MA(4) model with nonzero MA coefficients at lags 1 and 4 (an no constant term),
where the innovation distribution is Gaussian with constant variance.
Mdl = arima('MALags',[1,4],'Constant',0)
Mdl =
arima with properties:
Description: "ARIMA(0,0,4) Model (Gaussian Distribution)"
SeriesName: "Y"
Distribution: Name = "Gaussian"
P: 0
D: 0
Q: 4
Constant: 0
AR: {}
SAR: {}
MA: {NaN NaN} at lags [1 4]
SMA: {}
Seasonality: 0
Beta: [1×0]
Variance: NaN
The output shows the nonzero AR coefficients at lags 1 and 4, as specified. The property Q is equal to 4, the number of presample innovations needed to initialize the MA model. The unconstrained parameters are equal to NaN.
Display the value of MA:
Mdl.MA
ans=1×4 cell array
{[NaN]} {[0]} {[0]} {[NaN]}
The MA cell array returns four elements. The first and last elements (corresponding to lags 1 and 4) have value NaN, indicating these coefficients are nonzero and need to be estimated or otherwise specified by the user. arima sets the coefficients at interim lags equal to zero to maintain consistency with MATLAB® cell array indexing.
MA Model with Known Parameter Values
This example shows how to specify an MA(q) model with known parameter values. You can use such a fully specified model as an input to simulate or forecast.
Specify the MA(4) model
where the innovation distribution is Gaussian with constant variance 0.15.
Mdl = arima('Constant',0.1,'MA',{0.7,0.2},... 'MALags',[1,4],'Variance',0.15)
Mdl =
arima with properties:
Description: "ARIMA(0,0,4) Model (Gaussian Distribution)"
SeriesName: "Y"
Distribution: Name = "Gaussian"
P: 0
D: 0
Q: 4
Constant: 0.1
AR: {}
SAR: {}
MA: {0.7 0.2} at lags [1 4]
SMA: {}
Seasonality: 0
Beta: [1×0]
Variance: 0.15
All parameter values are specified, that is, no object property is NaN-valued.
MA Model with t Innovation Distribution
This example shows how to specify an MA(q) model with a Student's t innovation distribution.
Specify an MA(2) model with no constant term,
where the innovation process follows a Student's t distribution with eight degrees of freedom.
tdist = struct('Name','t','DoF',8); Mdl = arima('Constant',0,'MALags',1:2,'Distribution',tdist)
Mdl =
arima with properties:
Description: "ARIMA(0,0,2) Model (t Distribution)"
SeriesName: "Y"
Distribution: Name = "t", DoF = 8
P: 0
D: 0
Q: 2
Constant: 0
AR: {}
SAR: {}
MA: {NaN NaN} at lags [1 2]
SMA: {}
Seasonality: 0
Beta: [1×0]
Variance: NaN
The value of Distribution is a struct array with field Name equal to 't' and field DoF equal to 8. When you specify the degrees of freedom, they aren't estimated if you input the model to estimate.
Specify MA Model Using Econometric Modeler App
In the Econometric Modeler app, you can specify the lag structure, presence of a constant, and innovation distribution of an MA(q) model by following these steps. All specified coefficients are unknown but estimable parameters.
At the command line, open the Econometric Modeler app.
econometricModeler
Alternatively, open the app from the apps gallery (see Econometric Modeler).
In the Time Series pane, select the response time series to which the model will be fit.
On the Econometric Modeler tab, in the Models section, click MA.
The MA Model Parameters dialog box appears.

Specify the lag structure. To specify an MA(q) model that includes all MA lags from 1 through q, use the Lag Order tab. For the flexibility to specify the inclusion of particular lags, use the Lag Vector tab. For more details, see Specifying Univariate Lag Operator Polynomials Interactively. Regardless of the tab you use, you can verify the model form by inspecting the equation in the Model Equation section.
For example:
To specify an MA(3) model that includes a constant, includes the first lag, and has a Gaussian innovation distribution, set Moving Average Order to
3.To specify an MA(2) model that includes the first lag, has a Gaussian distribution, but does not include a constant:
Set Moving Average Order to
2.Clear the Include Constant Term check box.
To specify an MA(4) model containing nonconsecutive lags
where εt is a series of IID Gaussian innovations:
Click the Lag Vector tab.
Set Moving Average Order to
1 4.Clear the Include Constant Term check box.
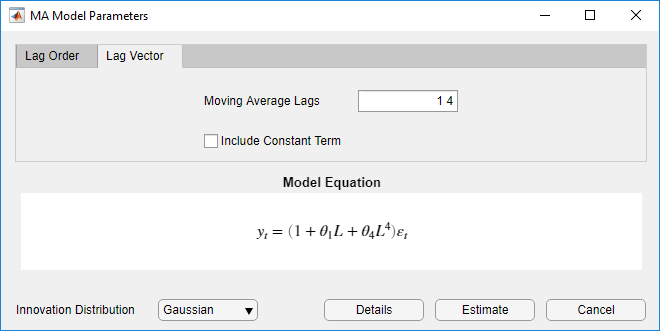
To specify an MA(2) model that includes the first lag, includes a constant term, and has t-distributed innovations:
Set Moving Average Lags to
2.Click the Innovation Distribution button, then select
t.
The degrees of freedom parameter of the t distribution is an unknown but estimable parameter.
After you specify a model, click Estimate to estimate all unknown parameters in the model.
What Are Moving Average Models?
MA(q) Model
The moving average (MA) model captures serial autocorrelation in a time series yt by expressing the conditional mean of yt as a function of past innovations, . An MA model that depends on q past innovations is called an MA model of degree q, denoted by MA(q).
The form of the MA(q) model in Econometrics Toolbox™ is
| (1) |
In lag operator polynomial notation, . Define the degree q MA lag operator polynomial You can write the MA(q) model as
Invertibility of the MA Model
By Wold’s decomposition [2], an MA(q) process is always stationary because is a finite-degree polynomial.
For a given process, however, there is no unique MA polynomial—there is always a noninvertible and invertible solution [1]. For uniqueness, it is conventional to impose invertibility constraints on the MA polynomial. Practically speaking, choosing the invertible solution implies the process is causal. An invertible MA process can be expressed as an infinite-degree AR process, meaning only past events (not future events) predict current events. The MA operator polynomial is invertible if all its roots lie outside the unit circle.
Econometrics Toolbox enforces invertibility of the MA polynomial. When you specify an MA
model using arima, you get an error if you enter coefficients
that do not correspond to an invertible polynomial. Similarly,
estimate imposes invertibility constraints during
estimation.
References
[1] Hamilton, James D. Time Series Analysis. Princeton, NJ: Princeton University Press, 1994.
[2] Wold, Herman. "A Study in the Analysis of Stationary Time Series." Journal of the Institute of Actuaries 70 (March 1939): 113–115. https://doi.org/10.1017/S0020268100011574.
See Also
Apps
Objects
Functions
Topics
- Analyze Time Series Data Using Econometric Modeler
- Specifying Univariate Lag Operator Polynomials Interactively
- Creating Univariate Conditional Mean Models
- Modify Properties of Conditional Mean Model Objects
- Specify Conditional Mean Model Innovation Distribution
- Plot the Impulse Response Function of Conditional Mean Model