Model Exchange Rate Volatility

Plot Exchange Rate Data

Load the Data_ExchangeRates.mat data set, provided by Haver Analytics®, which contains historical monthly prices in US dollars of the Euro, British Pound, Swiss Franc, Indian Rupee, and Chinese Yuan. Plot the series.

load Data_ExchangeRates

plot(dates,Data,LineWidth=1.5)
xline(datetime(1973,3,1),"r-","End Bretton Woods")
xline(datetime(1999,1,1),"b-","Start Euro")
ylabel("Price (US$)")
title("Exchange Rates (US$ / Monetary Unit)")
legend(series)
grid on

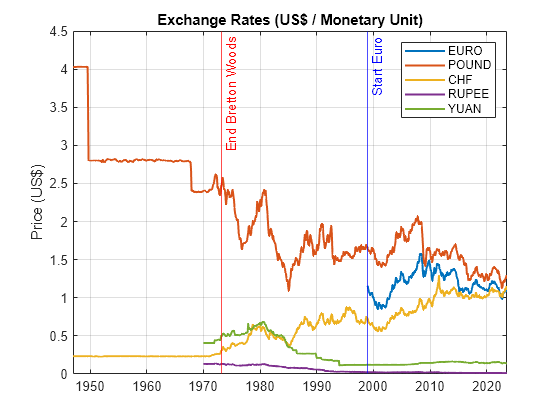
The series exhibit pronounced volatility and, during periods of persistently high or low volatility, volatility clustering.

Measure Volatility

A common measure of exchange rate volatility is the sample standard deviation of the percentage daily returns.

Plot the volatility for any of the exchange rate series during the period since the introduction of the Euro. This example uses the euro exchange rate; you can use the drop-down list control to choose a different series. The plotcolor function in the Supporting Function section facilitates series colors and legends for the plot.

euroEra = (dates >= datetime(1999,1,1));
euroDates = dates(euroEra);
rate =Data(euroEra,1);    % Select currency
returns = 100*price2ret(rate); % Percentage daily returns

figure
tiledlayout(1,2)
nexttile
h1 = plot(euroDates(2:end),returns); 
title("Percentage Daily Returns")
nexttile
h2 = histogram(returns); 
title("Volatility = " + std(returns))
color = plotcolor(Data,rate,h1,h2);

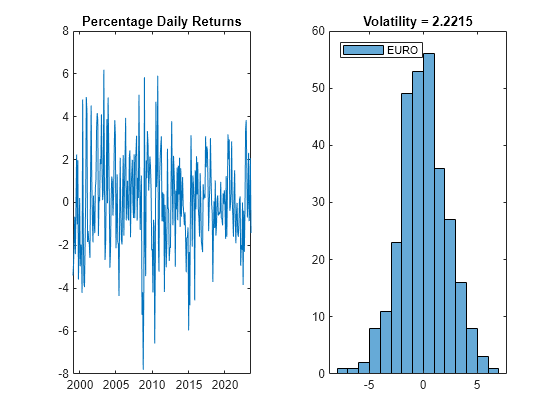
The spread of the distribution shows the overall volatility of the currency during the Euro period. More locally, returns in successive months fluctuate and show little autocorrelation.

Confirm this visual conclusion by computing the autocorrelation of the returns at lag 1.

acf = autocorr(returns);
lag1Autocorrelation = acf(2) % Lag 1 autocorrelation

lag1Autocorrelation = 
0.2967

The squared residuals of the returns measure the magnitude of the fluctuations of the series, and autocorrelation in the squared residuals indicates volatility clustering.

Plot the autocorrelation function (ACF) of the squared residuals.

residuals = returns - mean(returns);    % Residuals
residuals2 = residuals.^2;

figure
[~,~,~,h] = autocorr(residuals2,NumLags=10);
h(1).Color=color;
title("Squared Residual Autocorrelation")

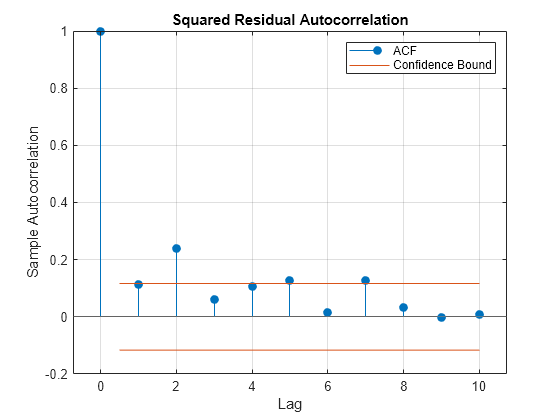
Although the autocorrelation of the returns is low, the magnitude of the fluctuations shows significant autocorrelation with recent lags.

Conduct a Ljung-Box Q-test, which provides a portmanteau statistical test of significance for autocorrelation. For details, see What Is the Ljung-Box Q-Test?.

[hlbq,pValue,stat,cValue] = lbqtest(residuals2)

hlbq = logical
   1

pValue = 
1.8348e-04

stat = 
50.5694

cValue = 
31.4104

A logical inference of hlbq = 1 is a rejection of the null hypothesis of no significant autocorrelations.

Fit GARCH Model of Returns

Common random walk models with innovations of fixed variance are insufficient to capture volatility clustering. GARCH models incorporate an innovations process that is conditional on innovations in previous time periods. As such, they can effectively capture the volatility clustering observed in exchange rate series.

Fit a GARCH(1,1) model to the residual returns using the estimate function.

Mdl = garch(1,1);
EstMdl = estimate(Mdl,residuals);

 
    GARCH(1,1) Conditional Variance Model (Gaussian Distribution):
 
                 Value      StandardError    TStatistic      PValue  
                ________    _____________    __________    __________

    Constant     0.23303       0.15177         1.5354         0.12468
    GARCH{1}     0.85478      0.056554         15.114      1.3016e-51
    ARCH{1}     0.098764      0.041237          2.395         0.01662

See Specify GARCH Models for a discussion of alternative specifications.

Compute the conditional variances of the model by using the infer function.

condVar = infer(EstMdl,residuals);
condVol = sqrt(condVar); % Conditional volatility

figure
tl = tiledlayout(2,1);
nexttile
h1 = plot(euroDates(2:end),residuals,Color=color);
title("Residual Returns")
nexttile
h2 = plot(euroDates(2:end),condVol,"r");
title("Conditional Volatility")
tl.TileSpacing = "compact";
tl.Padding = "compact";

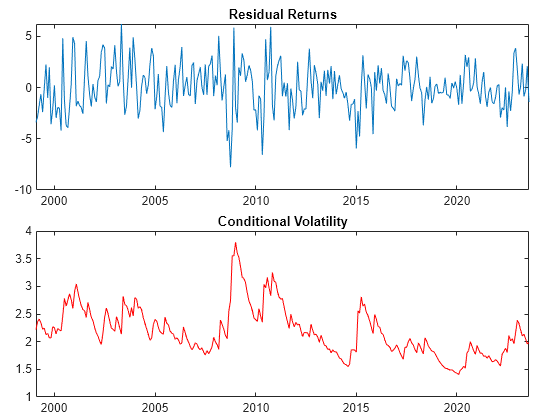
Peaks in the conditional volatility correspond to high-volatility clustering in the returns.

Plot the ACF the squared standardized residuals.

stdResiduals = residuals./condVol; % Standardized residuals

figure
[~,~,~,h] = autocorr(stdResiduals.^2,NumLags=10); % Show 10 most recent lags
set(h(1),Color=color);

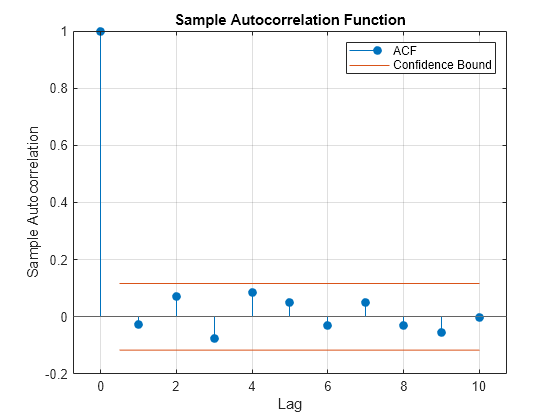
The ACF of the squared standardized residuals exhibit significantly reduced autocorrelation, which indicates a good fit.

Forecast GARCH Model

Compute minimum mean squared error forecasts of the conditional variance into a 2 year (24 month) horizon by using the forecast function.

horizon = 24; 
forVar = forecast(EstMdl,horizon,residuals);

figure
hold on
plot(dates(end-100:end),condVar(end-100:end),"r") % 100 most recent months
plot((dates(end)+calmonths(1)):calmonths(1):(dates(end)+calmonths(horizon)), ...
    forVar,"r--",LineWidth=1.5);
hold off
title("Conditional Variance Forecast")
legend(["Model" "Forecast"])

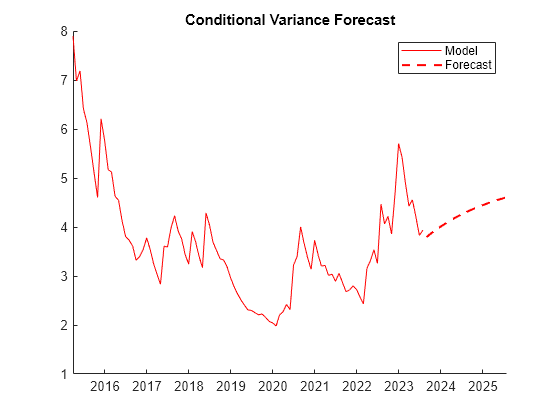
Volatility is only one component of exchange rate models. Using data on economic fundamentals of the nations involved in trade, you can construct more robust predictive models by combining GARCH models with mean models containing relevant exogenous predictors. See Specify Conditional Mean and Variance Models.

Supporting Function

This function assigns a color and legend to the selected exchange rate series.

function color = plotcolor(Data,rate,h1,h2)

C = colororder;

switch rate(end)

    case Data(end,1)
        color = C(1,:);
        legend(h2,"EURO",Location="northwest")

    case Data(end,2)
        color = C(2,:);
        legend(h2,"POUND",Location="northwest")

    case Data(end,3)
        color = C(3,:);
        legend(h2,"CHF",Location="northwest")

    case Data(end,4)
        color = C(4,:);
        legend(h2,"RUPEE",Location="northwest")

    case Data(end,5)
        color = C(5,:);
        legend(h2,"YUAN",Location="northwest")

end

h1.Color = color;
h2.FaceColor = color;

end