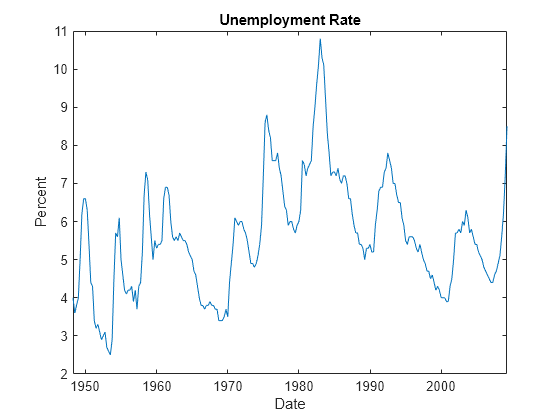
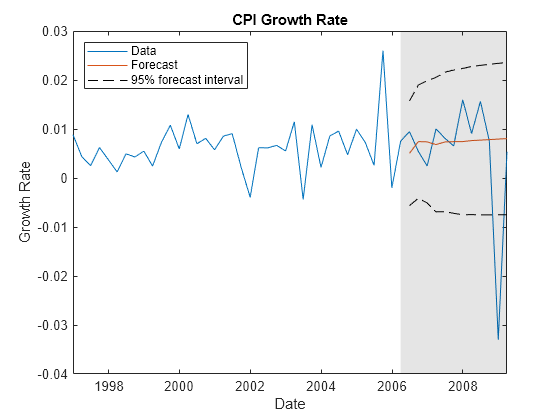
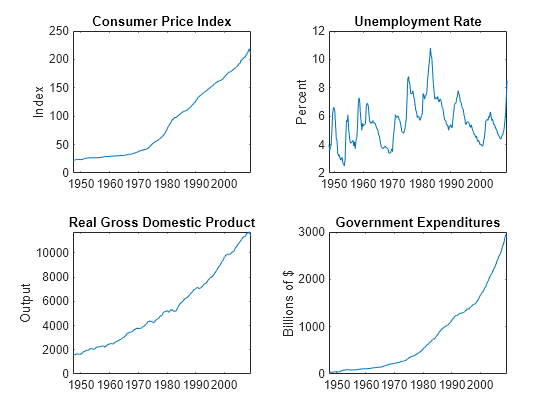
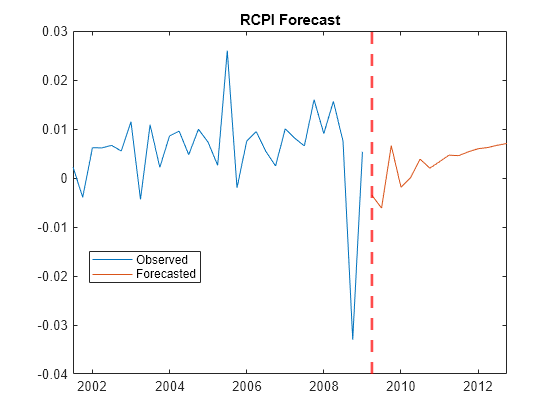
forecast
Forecast vector autoregression (VAR) model responses
Syntax
Description
Conditional and Unconditional Forecasts for Numeric Arrays
Y = forecast(Mdl,numperiods,Y0)Y over a length
numperiods forecast horizon, using the fully specified
VAR(p) model Mdl. The forecasted
responses represent the continuation of the presample data in the numeric array
Y0.
Y = forecast(Mdl,numperiods,Y0,Name=Value)forecast returns numeric arrays when all optional
input data are numeric arrays. For example,
forecast(Mdl,10,Y0,X=Exo) returns a numeric array
containing a 10-period forecasted response path from Mdl
and the numeric matrix of presample response data Y0, and
specifies the numeric matrix of future predictor data for the model regression
component in the forecast horizon Exo.
To produce a conditional forecast, specify future response data in a numeric
array by using the YF name-value argument.
Unconditional Forecasts for Tables and Timetables
Tbl2 = forecast(Mdl,numperiods,Tbl1)Tbl2 containing the length
numperiods paths of multivariate MMSE response variable
forecasts, which result from computing unconditional forecasts from the VAR
model Mdl. forecast uses the table
or timetable of presample data Tbl1 to initialize the
response series. (since R2022b)
forecast selects the variables in
Mdl.SeriesNames to forecast, or it selects all variables
in Tbl1. To select different response variables in
Tbl1 to forecast, use the
PresampleResponseVariables name-value argument.
Tbl2 = forecast(Mdl,numperiods,Tbl1,Name=Value)forecast(Mdl,10,Tbl1,PresampleResponseVariables=["GDP"
"CPI"]) returns a timetable of response variables containing their
unconditional forecasts from the VAR model Mdl, initialized
by the data in the GDP and CPI variables
of the timetable of presample data in Tbl1. (since R2022b)
Conditional Forecasts for Tables and Timetables
Tbl2 = forecast(Mdl,numperiods,Tbl1,InSample=InSample,ResponseVariables=ResponseVariables)Tbl2 containing the length
numperiods paths of multivariate MMSE response variable
forecasts and corresponding forecast MSEs, which result from computing
conditional forecasts from the VAR model Mdl.
forecast uses the table or timetable of presample
data Tbl1 to initialize the response series.
InSample is a table or timetable of future data in the
forecast horizon that forecast uses to compute
conditional forecasts and ResponseVariables specifies the
response variables in InSample. (since R2022b)
Tbl2 = forecast(Mdl,numperiods,Tbl1,InSample=InSample,ResponseVariables=ResponseVariables,Name=Value)
Examples
Return Matrix of VAR Model Forecasts
Fit a VAR(4) model to the consumer price index (CPI) and unemployment rate. Then, forecast unconditional MMSE responses from the estimated model. Supply all required data in numeric matrices.
Load the Data_USEconModel data set.
load Data_USEconModel dts = datetime(dates,ConvertFrom="datenum");
Plot the two series on separate plots.
figure plot(dts,DataTimeTable.CPIAUCSL); title("Consumer Price Index") ylabel("Index") xlabel("Date")
figure plot(dts,DataTimeTable.UNRATE); title("Unemployment Rate") ylabel("Percent") xlabel("Date")
Stabilize the CPI by converting it to a series of growth rates. Synchronize the two series by removing the first observation from the unemployment rate series.
RCPI = price2ret(DataTimeTable.CPIAUCSL); UNRATE = DataTimeTable.UNRATE(2:end); dts = dts(2:end); EstY = [RCPI UNRATE];
Create a default VAR(4) model by using the shorthand syntax.
Mdl = varm(2,4);
Estimate the model using the entire data set.
EstMdl = estimate(Mdl,EstY);
EstMdl is a fully specified, estimated varm model object.
Forecast responses from the estimated model over a three-year horizon. Specify the entire data set as presample observations.
numperiods = 12; Y0 = EstY; Y = forecast(EstMdl,numperiods,Y0);
Y is a 12-by-2 matrix of forecasted responses. The first and second columns contain the forecasted CPI growth rate and unemployment rate, respectively.
Plot the forecasted responses and the last 50 true responses.
fh = dateshift(dts(end),"end","quarter",1:numperiods); figure h1 = plot(dts((end-49):end),EstY((end-49):end,1)); hold on h2 = plot(fh,Y(:,1)); title("CPI Growth Rate") ylabel("Growth Rate") xlabel("Date") h = gca; fill([dts(end) fh([end end]) dts(end)],h.YLim([1 1 2 2]),"k", ... FaceAlpha=0.1,EdgeColo="none"); legend([h1 h2],"Data","Forecast") hold off
figure h1 = plot(dts((end-49):end),EstY((end-49):end,2)); hold on h2 = plot(fh,Y(:,2)); title("Unemployment Rate") ylabel("Percent") xlabel("Date") h = gca; fill([dts(end) fh([end end]) dts(end)],h.YLim([1 1 2 2]),"k", ... FaceAlpha=0.1,EdgeColo="none"); legend([h1 h2],"True","Forecast",Location="northwest") hold off
Compute Conditional Forecasts from Numeric Matrix of Future Response Data
This example is based on Return Matrix of VAR Model Forecasts. Forecast MMSE responses of the consumer price index (CPI) growth rate four quarters beyond the sampling data, given that the unemployment rate is 8% for each future quarter in the forecast horizon.
Load the Data_USEconModel data set.
load Data_USEconModel dts = datetime(dates,ConvertFrom="datenum");
Stabilize the CPI by converting it to a series of growth rates. Synchronize the two series by removing the first observation from the unemployment rate series.
RCPI = price2ret(DataTimeTable.CPIAUCSL); UNRATE = DataTimeTable.UNRATE(2:end); dts = dts(2:end); EstY = [RCPI UNRATE];
Create a default VAR(4) model using the shorthand syntax. Estimate the model using the entire data set.
Mdl = varm(2,4); EstMdl = estimate(Mdl,EstY);
Forecast the CPI growth rate from the estimated model over a one-year horizon, given that the unemployment rate over the next year is 8% each quarter. Create a 2-by-4 matrix CondYF containing the conditions in the forecast horizon, in which the first column (corresponding to RCPI) is composed of NaN values and the second column (corresponding to UNRATE) is completely composed of 8. Supply the future data to forecast and specify the entire data set as presample observations.
numperiods = 4; Y0 = EstY; CondYF = NaN(numperiods,Mdl.NumSeries); CondYF(:,2) = 8; Y = forecast(EstMdl,numperiods,Y0,YF=CondYF)
Y = 4×2
-0.0068 8.0000
-0.0121 8.0000
0.0006 8.0000
-0.0045 8.0000
Y is a 4-by-2 matrix of the forecasted CPI growth rate series into the next year, with the unemployment rate fixed at 8%.
Estimate Forecast Intervals
Analyze forecast accuracy using forecast intervals over a three-year horizon. This example follows from Return Matrix of VAR Model Forecasts.
Load the Data_USEconModel data set and preprocess the data.
load Data_USEconModel dts = datetime(dates,ConvertFrom="datenum"); RCPI = price2ret(DataTimeTable.CPIAUCSL); UNRATE = DataTimeTable.UNRATE(2:end); D = [RCPI UNRATE];
Estimate a VAR(4) model of the two response series. Reserve the last three years of data.
bfh = dts(end) - years(3); estIdx = dts < bfh; Mdl = varm(2,4); EstY = D(estIdx,:); EstMdl = estimate(Mdl,EstY);
Forecast responses from the estimated model over a three-year horizon. Specify the entire data set as presample observations. Return the MSE of the forecasts.
numperiods = 12; [Y,YMSE] = forecast(EstMdl,numperiods,EstY);
Y is a 12-by-2 matrix of forecasted responses. YMSE is a 12-by-1 cell vector of corresponding MSE matrices.
Extract the main diagonal elements from the matrices in each cell of YMSE. Apply the square root of the result to obtain standard errors.
extractMSE = @(x)diag(x)'; MSE = cellfun(extractMSE,YMSE,UniformOutput=false); SE = sqrt(cell2mat(MSE));
Estimate approximate 95% forecast intervals for each response series.
YFI = zeros(numperiods,Mdl.NumSeries,2); YFI(:,:,1) = Y - 2*SE; YFI(:,:,2) = Y + 2*SE;
Plot the forecasted responses and the last 50 true responses.
figure h1 = plot(dts((end-49):end),RCPI((end-49):end)); hold on; h2 = plot(dts(~estIdx),Y(:,1)); h3 = plot(dts(~estIdx),YFI(:,1,1),"k--"); plot(dts(~estIdx),YFI(:,1,2),"k--"); title("CPI Growth Rate") ylabel("Growth Rate") xlabel("Date") h = gca; fill([bfh h.XLim([2 2]) bfh],h.YLim([1 1 2 2]),"k", ... FaceAlpha=0.1,EdgeColor="none"); legend([h1 h2 h3],"Data","Forecast","95% forecast interval", ... Location="northwest") hold off
figure h1 = plot(dts((end-49):end),UNRATE((end-49):end)); hold on; h2 = plot(dts(~estIdx),Y(:,2)); h3 = plot(dts(~estIdx),YFI(:,2,1),"k--"); plot(dts(~estIdx),YFI(:,2,2),"k--"); title('Unemployment Rate') ylabel('Percent') xlabel('Date') h = gca; fill([bfh h.XLim([2 2]) bfh],h.YLim([1 1 2 2]),"k", ... FaceAlpha=0.1,EdgeColor="none"); legend([h1 h2 h3],"Data","Forecast","95% forecast interval", ... Location="northwest") hold off
Return Timetable of Forecasts and Array of Forecast MSEs
Since R2022b
Fit a VAR(4) model to the consumer price index (CPI) and unemployment rate. Then, forecast unconditional MMSE responses from the estimated model. Supply all required data in timetables. This example is based on Return Response Series in Matrix from Unconditional Simulation.
Load and Preprocess Data
Load the Data_USEconModel data set. Compute the CPI growth rate. Because the growth rate calculation consumes the earliest observation, include the rate variable in the timetable by prepending the series with NaN.
load Data_USEconModel
DataTimeTable.RCPI = [NaN; price2ret(DataTimeTable.CPIAUCSL)];Prepare Timetable for Estimation
When you plan to supply a timetable directly to estimate, you must ensure it has all the following characteristics:
All selected response variables are numeric and do not contain any missing values.
The timestamps in the
Timevariable are regular, and they are ascending or descending.
Remove all missing values from the table, relative to the CPI rate (RCPI) and unemployment rate (UNRATE) series.
varnames = ["RCPI" "UNRATE"]; DTT = rmmissing(DataTimeTable,DataVariables=varnames); numobs = height(DTT)
numobs = 245
rmmissing removes the four initial missing observations from the DataTimeTable to create a sub-table DTT. The variables RCPI and UNRATE of DTT do not have any missing observations.
Determine whether the sampling timestamps have a regular frequency and are sorted.
areTimestampsRegular = isregular(DTT,"quarters")areTimestampsRegular = logical
0
areTimestampsSorted = issorted(DTT.Time)
areTimestampsSorted = logical
1
areTimestampsRegular = 0 indicates that the timestamps of DTT are irregular. areTimestampsSorted = 1 indicates that the timestamps are sorted. Macroeconomic series in this example are timestamped at the end of the month. This quality induces an irregularly measured series.
Remedy the time irregularity by shifting all dates to the first day of the quarter.
dt = DTT.Time; dt = dateshift(dt,"start","quarter"); DTT.Time = dt; areTimestampsRegular = isregular(DTT,"quarters")
areTimestampsRegular = logical
1
DTT is regular with respect to time.
Create Model Template for Estimation
Create a default VAR(4) model by using the shorthand syntax. Specify the response variable names.
Mdl = varm(2,4); Mdl.SeriesNames = varnames;
Fit Model to Data
Estimate the model. Pass the entire timetable DTT. By default, estimate selects the response variables in Mdl.SeriesNames to fit to the model. Alternatively, you can use the ResponseVariables name-value argument.
EstMdl = estimate(Mdl,DTT);
Forecast Responses and Compute Forecast MSEs
Forecast responses from the estimated model over a three-year horizon. Specify the entire data set DTT as a presample observations.
numperiods = 12; [Tbl2,YMSE] = forecast(EstMdl,numperiods,DTT); Tbl2
Tbl2=12×2 timetable
Time RCPI_Responses UNRATE_Responses
_____ ______________ ________________
Q2-09 -0.0078947 8.7104
Q3-09 -0.014099 8.6682
Q4-09 -0.00036087 7.9762
Q1-10 -0.0025178 7.3152
Q2-10 -0.00074203 6.6233
Q3-10 0.0039157 5.9685
Q4-10 0.0043404 5.4787
Q1-11 0.0056518 5.1184
Q2-11 0.0070472 4.8808
Q3-11 0.007241 4.7632
Q4-11 0.0075783 4.728
Q1-12 0.0077906 4.7519
YMSE
YMSE=12×1 cell array
{2x2 double}
{2x2 double}
{2x2 double}
{2x2 double}
{2x2 double}
{2x2 double}
{2x2 double}
{2x2 double}
{2x2 double}
{2x2 double}
{2x2 double}
{2x2 double}
Tbl2 is a 12-by-2 timetable of forecasted CPI growth and unemployment rates. Forecast variable names are appended with _Responses, for example, RCPI_Responses contains the forecasts of RCPI. The timestamps of Tbl2 follow directly from the timestamps of DTT, and they have the same sampling frequency.
YMSE is a 12-by-1 cell vector of corresponding 2-by-2 forecast MSE matrices for each period in the forecast horizon. For example, the forecast covariance between each response series in period 6 for the forecast horizon (off diagonal of YMSE{6}) is –0.0025.
Forecast VARX(4) Model
Since R2022b
Estimate a four-degree vector autoregression model including exogenous predictors (VARX(4)) of the consumer price index (CPI), the unemployment rate, and the gross domestic product (GDP). Include a linear regression component containing the current quarter and the last four quarters of government consumption expenditures and investment (GCE). Forecast a response path from the estimated model.
Load the Data_USEconModel data set. Compute the real GDP.
load Data_USEconModel
DataTimeTable.RGDP = DataTimeTable.GDP./DataTimeTable.GDPDEF*100;Plot all variables on separate plots.
figure tiledlayout(2,2) nexttile plot(DataTimeTable.Time,DataTimeTable.CPIAUCSL); ylabel("Index") title("Consumer Price Index") nexttile plot(DataTimeTable.Time,DataTimeTable.UNRATE); ylabel("Percent") title("Unemployment Rate") nexttile plot(DataTimeTable.Time,DataTimeTable.RGDP); ylabel("Output") title("Real Gross Domestic Product") nexttile plot(DataTimeTable.Time,DataTimeTable.GCE); ylabel("Billions of $") title("Government Expenditures")
Stabilize the CPI, GDP, and GCE by converting each to a series of growth rates. Synchronize the unemployment rate series with the others by removing its first observation.
varnames = ["CPIAUCSL" "RGDP" "GCE"]; DTT = varfun(@price2ret,DataTimeTable,InputVariables=varnames); DTT.Properties.VariableNames = varnames; DTT.UNRATE = DataTimeTable.UNRATE(2:end);
Make the time base regular.
dt = DTT.Time; dt = dateshift(dt,"start","quarter"); DTT.Time = dt;
Expand the GCE rate series to a matrix that includes the first lagged series through the fourth lag series.
RGCELags = lagmatrix(DTT,1:4,DataVariables="GCE");
DTT = [DTT RGCELags];
DTT = rmmissing(DTT);Create separate presample and estimation sample data sets. The presample contains the earliest p = 4 observations, and the estimation sample contains the rest of the data.
p = 4; PS = DTT(1:p,:); InSample = DTT((p+1):end,:); respnames = ["CPIAUCSL" "UNRATE" "RGDP"]; idx = endsWith(InSample.Properties.VariableNames,"GCE"); prednames = InSample.Properties.VariableNames(idx);
Create a default VAR(4) model by using the shorthand syntax. Specify the response variable names.
Mdl = varm(3,p); Mdl.SeriesNames = respnames;
Estimate the model using all but the last three years of data. Specify the GCE matrix as data for the regression component.
bfh = DTT.Time(end) - years(3);
estIdx = DTT.Time < bfh;
EstMdl = estimate(Mdl,DTT(estIdx,:),ResponseVariables=respnames, ...
PredictorVariables=prednames);Forecast a path of quarterly responses three years into the future.
numperiods = 12;
Tbl1 = DTT(estIdx,:);
Tbl2 = forecast(EstMdl,numperiods,Tbl1,InSample=DTT(~estIdx,:), ...
PredictorVariables=prednames);Tbl1 is a 12-by-3 timetable of forecasted responses. Variables names correspond to the response variable names in respnames appended with _Responses.
Plot the forecasted responses and the last 50 true responses.
figure tiledlayout(2,2) for j = 1:Mdl.NumSeries nexttile h1 = plot(DTT.Time((end-49):end),DTT{(end-49):end,respnames(j)}); hold on h2 = plot(DTT.Time(~estIdx),Tbl2{:,respnames(j)+"_Responses"}); title(respnames(j)) h = gca; fill([bfh h.XLim([2 2]) bfh],h.YLim([1 1 2 2]),"k", ... FaceAlpha=0.1,EdgeColor="none"); hold off end hl = legend([h1 h2],["Data" "Forecast"]); hl.Position = [0.6 0.25 hl.Position(3:4)];
Return Timetable of Conditional Forecasts
Since R2022b
Compute conditional forecasts of the VAR model in Return Timetable of Responses and Innovations from Unconditional Simulation, in which economists hypothesize that the unemployment rate is 6% for 15 quarters after the end of the sample (from Q2 of 2009 through Q4 of 2012).
Load and Preprocess Data
Load the Data_USEconModel data set. Compute the CPI growth rate. Because the growth rate calculation consumes the earliest observation, include the rate variable in the timetable by prepending the series with NaN.
load Data_USEconModel
DataTimeTable.RCPI = [NaN; price2ret(DataTimeTable.CPIAUCSL)];Prepare Timetable for Estimation
Remove all missing values from the table, relative to the CPI rate (RCPI) and unemployment rate (UNRATE) series.
varnames = ["RCPI" "UNRATE"]; DTT = rmmissing(DataTimeTable,DataVariables=varnames);
Remedy the time irregularity by shifting all dates to the first day of the quarter.
dt = DTT.Time; dt = dateshift(dt,"start","quarter"); DTT.Time = dt;
Create Model Template for Estimation
Create a default VAR(4) model using the shorthand syntax. Specify the response variable names.
p = 4; Mdl = varm(2,p); Mdl.SeriesNames = varnames;
Fit Model to Data
Estimate the model. Pass the entire timetable DTT. By default, estimate selects the response variables in Mdl.SeriesNames to fit to the model. Alternatively, you can use the ResponseVariables name-value argument.
EstMdl = estimate(Mdl,DTT);
Prepare for Conditional Forecast of Estimated Model
Suppose economists hypothesize that the unemployment rate will be at 6% for the next 15 quarters.
Create a timetable with the following qualities:
The timestamps are regular with respect to the estimation sample timestamps and they are ordered from Q2 of 2009 through Q4 of 2012.
The variable
RCPI(and, consequently, all other variables inDTT) is a 15-by-1 vector ofNaNvalues.The variable
UNRATEis a 15-by-1 vector, where each element is 6.
numperiods = 15;
fhdt = DTT.Time(end) + calquarters(1:numperiods);
DTTCondF = retime(DTT,fhdt,"fillwithmissing");
DTTCondF.UNRATE = ones(numperiods,1)*6;DTTCondF is a 15-by-15 timetable that follows directly, in time, from DTT, and both timetables have the same variables. All variables in DTTCondF contain NaN values, except for UNRATE, which is a vector composed of the value 6.
Compute Conditional Forecast of Estimated Model
Forecast the CPI growth rate given the hypothesis by supplying the conditioning data DTTCondF and specifying the response variable names. Supply the estimation sample as a presample to initialize the model.
rng(1) % For reproducibility Tbl2 = forecast(EstMdl,numperiods,DTT,InSample=DTTCondF, ... ResponseVariables=EstMdl.SeriesNames); size(Tbl2)
ans = 1×2
15 17
idx = endsWith(Tbl2.Properties.VariableNames,"_Responses");
head(Tbl2(:,idx)) Time RCPI_Responses UNRATE_Responses
_____ ______________ ________________
Q2-09 -0.0035362 6
Q3-09 -0.0061302 6
Q4-09 0.0066157 6
Q1-10 -0.0018704 6
Q2-10 3.7558e-05 6
Q3-10 0.003859 6
Q4-10 0.002009 6
Q1-11 0.0033291 6
Tbl2 is a 15-by-17 timetable of all variables in DTTCondF and the RCPI forecasts given UNRATE is 6% for the next 15 quarters. RCPI_Responses contains the forecast path. UNRATE_Responses is a vector composed of the value 6. All other variables in Tbl2 are the variables and their values in DTTCondF.
Plot the CPI growth rate forecast with the final few values of the estimation sample data.
figure h1 = plot(DTT.Time((end-30):end),DTT.RCPI((end-30):end)); hold on h2 = plot(Tbl2.Time,Tbl2.RCPI_Responses); xline(Tbl2.Time(1),"r--",LineWidth=2) hold off title("RCPI Forecast") legend([h1 h2(1)],["Observed" "Forecasted"], ... Location="best")
Return Multiple Conditional Forecast Paths
Since R2022b
Compute conditional forecasts of the VAR model in Return Timetable of Responses and Innovations from Unconditional Simulation, in which economists make several hypotheses on the value of the unemployment rate at a forecast horizon of one year.
Load the Data_USEconModel data set. Preprocess the response variables.
load Data_USEconModel
DataTimeTable.RCPI = [NaN; price2ret(DataTimeTable.CPIAUCSL)];Prepare the timetable for estimation.
varnames = ["RCPI" "UNRATE"]; DTT = rmmissing(DataTimeTable,DataVariables=varnames); dt = DTT.Time; dt = dateshift(dt,"start","quarter"); DTT.Time = dt;
Estimate the VAR(4) model.
p = 4; Mdl = varm(2,p); Mdl.SeriesNames = varnames; EstMdl = estimate(Mdl,DTT);
Consider generating several forecast paths of the CPI growth rate assuming the unemployment rate is 1%, 4%, 5%, 8%, and 10% percent throughout the forecast horizon.
Create a timetable with the following qualities:
The timestamps are regular with respect to the estimation sample timestamps and they are ordered from Q2 of 2009 through Q1 of 2010.
The variable
UNRATEis a 4-by-5 matrix, where each column is composed of each of the assumptions on the value of the unemployment rate in the forecast horizon; the elements of the first column are 1, elements of the second column are 4, and so on.The variable
RCPIis a 4-by-5 matrix ofNaNvalues to be filled with forecasted paths.All other variables are
NaN-valued vectors.
numperiods = 4;
fhdt = DTT.Time(end) + calquarters(1:numperiods);
DTTCondF = retime(DTT,fhdt,"fillwithmissing");
DTTCondF.UNRATE = ones(numperiods,1)*[1 4 5 8 10];
DTTCondF.RCPI = nan(numperiods,width(DTTCondF.UNRATE));DTTCondF is a 4-by-15 timetable that follows directly, in time, from DTT, and both timetables have the same variables. All variables in DTTCondF contain NaN values, except for UNRATE, which is a 4-by-5 matrix of the hypothesized values of the unemployment rate in the forecast horizon.
Forecast the CPI growth rate given the hypotheses by supplying the conditioning data DTTCondF and specifying the response variable names. Supply the estimation sample as a presample to initialize the model. Return the forecast MSE matrices.
rng(1) % For reproducibility [Tbl2,YMSE] = forecast(EstMdl,numperiods,DTT,InSample=DTTCondF, ... ResponseVariables=EstMdl.SeriesNames); size(Tbl2)
ans = 1×2
4 17
idx = endsWith(Tbl2.Properties.VariableNames,"_Responses");
head(Tbl2(:,idx)) Time RCPI_Responses UNRATE_Responses
_____ _____________________________________________________________________ _________________________
Q2-09 0.0045044 -0.00031993 -0.001928 -0.0067524 -0.0099686 1 4 5 8 10
Q3-09 0.0087271 -0.00018729 -0.0031588 -0.012073 -0.018016 1 4 5 8 10
Q4-09 0.021614 0.012615 0.0096155 0.00061625 -0.0053833 1 4 5 8 10
Q1-10 0.0045863 0.00071227 -0.00057906 -0.0044531 -0.0070357 1 4 5 8 10
YMSE
YMSE=4×1 cell array
{2x2 double}
{2x2 double}
{2x2 double}
{2x2 double}
Tbl2 is a 4-by-17 timetable of all variables in DTTCondF. The RCPI forecasts, stored in the variable RCPI_Responses, is a 4-by-5 matrix of five forecast paths. Each path uses the corresponding assumption about the value of unemployment rate in UNRATE_Responses.
YMSE is a 4-by-1 cell vector of forecast MSE matrices for each period in the forecast horizon. The MSE matrices apply to each forecast path, and all elements of each matrix corresponding to the conditioning variable are 0.
Input Arguments
Output Arguments
Algorithms
forecastestimates unconditional forecasts using the equationwhere t = 1,...,
numperiods.forecastfilters anumperiods-by-numseriesmatrix of zero-valued innovations throughMdl.forecastuses specified presample innovations (Y0orTbl1) wherever necessary.forecastestimates conditional forecasts using the Kalman filter.forecastrepresents the VAR modelMdlas a state-space model (ssmmodel object) without observation error.forecastfilters the forecast dataYFthrough the state-space model. At period t in the forecast horizon, any unknown response iswhere s < t, is the filtered estimate of y from period s in the forecast horizon.
forecastuses specified presample values inY0orTbl1for periods before the forecast horizon.
The way
forecastdeterminesnumpaths, the number of paths (pages) in the output argumentY, or the number of paths (columns) in the forecasted response variables in the output argumentTbl2, depends on the forecast type.If you estimate unconditional forecasts, which means you do not specify the
YFname-value argument, orInSampleandResponseVariablesname-value arguments,numpathsis the number of paths in theY0orTbl1input argument.If you estimate conditional forecasts and the presample data
Y0and future sample dataYF, or response variables inTbl1andInSamplehave more than one path,numpathsis the fewest number of paths between the presample and future sample response data. Consequently,forecastuses only the firstnumpathspaths of each response variable for each input.If you estimate conditional forecasts and either
Y0orYF, or response variables inTbl1orInSamplehave one path,numpathsis the number of pages in the array with the most pages.forecastuses the variables with one path to produce each output path.
forecastsets the time origin of models that include linear time trends t0 tonumpreobs–Mdl.P(after removing missing values), wherenumpreobsis the number of presample observations. Therefore, the times in the trend component are t = t0 + 1, t0 + 2,..., t0 +numpreobs. This convention is consistent with the default behavior of model estimation in whichestimateremoves the firstMdl.Presponses, reducing the effective sample size. Althoughforecastexplicitly uses the firstMdl.Ppresample responses inY0orTbl1to initialize the model, the total number of usable observations determines t0. An observation inY0is usable if it does not contain aNaN.
References
[1] Hamilton, James D. Time Series Analysis. Princeton, NJ: Princeton University Press, 1994.
[2] Johansen, S. Likelihood-Based Inference in Cointegrated Vector Autoregressive Models. Oxford: Oxford University Press, 1995.
[3] Juselius, K. The Cointegrated VAR Model. Oxford: Oxford University Press, 2006.
[4] Lütkepohl, H. New Introduction to Multiple Time Series Analysis. Berlin: Springer, 2005.
Version History
Introduced in R2017a
You can also select a web site from the following list
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)
Asia Pacific
- Australia (English)
- India (English)
- New Zealand (English)
- 中国
- 日本Japanese (日本語)
- 한국Korean (한국어)