Overview of Interest-Rate Tree Models

Interest-Rate Modeling

Financial Instruments Toolbox™ computes prices and sensitivities of interest-rate contingent claims based on several methods of modeling changes in interest rates over time:

The interest-rate term structure
This model uses sets of zero-coupon bonds to predict changes in interest rates. A zero-coupon bond is a bond that, instead of carrying a coupon, is sold at a discount from its face value, pays no interest during its life, and pays the principal only at maturity.
Heath-Jarrow-Morton (HJM) model
The HJM model considers a given initial term structure of interest rates and a specification of the volatility of forward rates to build a tree representing the evolution of the interest rates, based on a statistical process.
Black-Derman-Toy (BDT) model
In the BDT model, all security prices and rates depend on the short rate (annualized one-period interest rate). The model uses long rates (the yield on a zero-coupon Treasury bond) and their volatilities to construct a tree of possible future short rates. The resulting tree can then be used to determine the value of interest-rate sensitive securities from this tree.
Hull-White (HW) model
The Hull-White model incorporates the initial term structure of interest rates and the volatility term structure to build a trinomial recombining tree of short rates. The resulting tree is used to value interest-rate dependent securities. The implementation of the HW model in Financial Instruments Toolbox is limited to one factor.
Black-Karasinski (BK) model
The BK model is a single-factor, log-normal version of the HW model.

For detailed information about interest-rate models, see:

Pricing Using Interest-Rate Term Structure for a discussion of price and sensitivity based on portfolios of zero-coupon bonds
Pricing Using Interest-Rate Tree Models for a discussion of price and sensitivity based on the HJM and BDT interest-rate models
Note
Historically, the initial version of Financial Instruments Toolbox provided only the HJM interest-rate model. A later version added the BDT model. The current version adds both the HW and BK models. This section provides extensive examples of using the HJM and BDT models to compute prices and sensitivities of interest-rate based financial derivatives.
The HW and BK tree structures are similar to the BDT tree structure. To avoid needless repetition throughout this section, documentation is provided only where significant deviations from the BDT structure exist. Specifically, HW and BK Tree Structures explains the few noteworthy differences among the various formats.

Rate and Price Trees

The interest-rate or price trees can be either binomial (two branches per node) or trinomial (three branches per node). Typically, binomial trees assume that underlying interest rates or prices can only either increase or decrease at each node. Trinomial trees allow for a more complex movement of rates or prices. With trinomial trees, the movement of rates or prices at each node is unrestricted (for example, up-up-up or unchanged-down-down). At any time step, the price or rate direction can be upward, neutral, or downward.

Types of Trees

Financial Instruments Toolbox trees can be classified as bushy or recombining. A bushy tree is a tree in which the number of branches increases exponentially relative to observation times; branches never recombine. In this context, a recombining tree is the opposite of a bushy tree. A recombining tree has branches that recombine over time. From any given node, the node reached by taking the path up-down is the same node reached by taking the path down-up. A bushy tree and a recombining binomial tree are illustrated next.

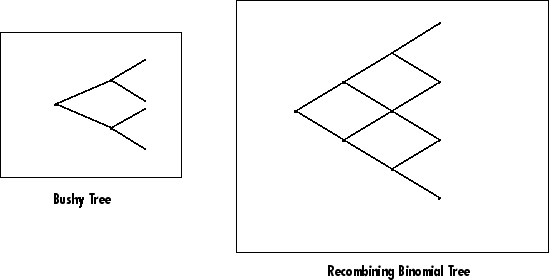
The Heath-Jarrow-Morton model works with bushy trees. The Black-Derman-Toy model, on the other hand, works with recombining binomial trees. The Hull-White and Black-Karasinsk interest-rate models work with recombining trinomial trees.

Viewing Rate or Price Movement

This toolbox provides the data file deriv.mat that contains four interest-rate based trees:

HJMTree — A bushy binomial tree
BDTTree — A recombining binomial tree
HWTree and BKTree — Recombining trinomial trees

The toolbox also provides the treeviewer function, which graphically displays the shape and data of price, interest rate, and cash flow trees. Viewed with treeviewer, the bushy shape of an HJM tree and the recombining shape of a BDT tree are apparent.

With treeviewer, you can also see the recombining shape of HW and BK trinomial trees.