CORDIC Square Root HDL Optimized
Libraries:
Fixed-Point Designer HDL Support /
Math Operations
Description
The CORDIC Square Root HDL Optimized block returns the square root of
u, computed using a CORDIC-based implementation optimized for HDL code
generation.
Examples
This example shows how to use the CORDIC Square Root HDL Optimized block to compute the square root of real non-negative scalars.
CORDIC-Based Square Root
The CORDIC Square Root HDL Optimized block uses a CORDIC algorithm in hyperbolic vectoring mode to compute the approximation of square root (see Compute Square Root Using CORDIC). This CORDIC-based algorithm is different from the Simulink® Sqrt block, which uses bisection and Newton-Raphson methods. The algorithm in the CORDIC Square Root HDL Optimized block requires only iterative shift-add operations.
I/O Interface
The CORDIC Square Root HDL Optimized block is fully-pipelined. It can accept input data on any cycle, including on consecutive clock cycles. Use validIn to indicate a valid input. When the block has finished the computation, it will change validOut to true for one clock cycle. For inputs sent on consecutive clock cycles, validOut will also be set to true on consecutive clock cycles.
Customizable CORDIC Maximum Shift Value and Number of Iterations Per Pipeline Register
This block uses iterative normalization and CORDIC algorithms. If the input is fixed point or scaled doubles, it uses multiple steps for computation. The normalization uses nextpow2(u.WordLength) iterations. The number of CORDIC iterations depends on the CORDIC maximum shift value. A larger word length can provide higher resolution but needs more iterations to process. This block can perform multiple iterations per pipeline stage. This results in smaller latency at cost of longer critical path in the generated HDL design.
For example, if the word length of the input u is 16, normalization requires 4 iterations. If the Automatically select CORDIC maximum shift value based on input word length parameter is selected, this block uses 16 - 1 = 15 as the CORDIC maximum shift value in the computation and it requires 17 iterations. The total number of iterations is 4 + 17 = 21 and the latency of the block is 2 + ceil(total number of iterations/nIterPerReg). If the number of iterations per pipeline register is set to 1, then the block latency is 23; if the number of iterations per pipeline register is set to 2, then the block latency is 13; etc. If the number of iterations per pipeline register is greater than or equal to the total number of required iterations, the block performs all iterations in one pipeline stage and the total latency is minimized to 3.
The total number of iterations and block latency can be calculated using the embblk.latency.cordicSqrtHDLOptimizedLatency function.
If the input is floating point, the block latency is 0.
Define Simulation Parameters
Specify the number of input samples.
numSamples = 10;
Specify the data type as fixed, scaledDouble, single, or double.
DT =  'fixed';
'fixed';For fixed-point data type, specify the word length and fraction length.
wordLength = 16; FractionLength = 10;
If the Automatically select CORDIC maximum shift value based on input word length parameter is not selected, define the maximum CORDIC shift value. For fixed point data types, this value cannot exceed wordLength - 1.
autoMaxVal =  "on";
maximumShiftValue = wordLength - 1;
"on";
maximumShiftValue = wordLength - 1;Generate Input Data
Generate input data u. The input value must be a real non-negative scalar.
rng('default');
u = abs(randn(1,numSamples));Cast to Selected Data Type
Cast the input data u to the selected data type.
switch lower(DT) case 'fixed' u = cast(u,'like',fi([],1,wordLength,FractionLength)); case 'scaleddouble' u = cast(u,'like',fi([],1,wordLength,FractionLength),'DataType','ScaledDouble'); case 'single' u = single(u); case 'double' u = double(u); otherwise u = double(u); end
Configure Block Pipeline
Check how many iterations the block requires for the selected data type.
[~, totalIterations] = embblk.latency.cordicSqrtHDLOptimizedLatency(u,1,maximumShiftValue)
totalIterations = 21
Define the number of iterations to be performed in one pipeline stage.
nIterPerReg = 1;
Open the Model
Open the CORDICSquareRootModel model.
model = 'CORDICSquareRootModel';
open_system(model);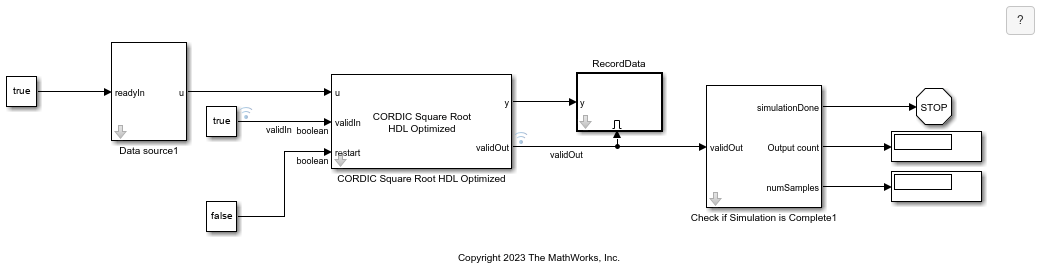
Simulate the Model
Configure the model workspace and run the simulation.
fixed.example.setModelWorkspace(model,'u',u,'numSamples',numSamples,'maximumShiftValue',maximumShiftValue,... 'nIterPerReg',nIterPerReg); set_param([model,'/CORDIC Square Root HDL Optimized'],'autoMaximumShiftVal',autoMaxVal); out = sim(model);
Verify Output Solutions
Compare the fixed-point result from the CORDIC Square Root HDL Optimized block with the floating-point result from the MATLAB® sqrt function.
yBuiltIn = sqrt(double(u))'; y = out.y(1:numSamples); absError = (double(y)-yBuiltIn)
absError = 10×1
10-3 ×
-0.1450
-0.7312
0.0029
-0.8692
0.2197
-0.9328
-0.2752
-0.5076
-0.9682
-0.1284
Block Latency
The block latency is the number of clock cycles between a successful input and when the corresponding output becomes valid. The latency of this block depends on the datatype, CORDIC maximum shift value, and Number of iterations per pipeline register.
Calculate the expected latency and total number of iterations. The CORDIC maximum shift value can be empty if the Automatically select CORDIC maximum shift value based on input word length parameter parameter is selected.
[explatency, ~] = embblk.latency.cordicSqrtHDLOptimizedLatency(u,nIterPerReg,maximumShiftValue)
explatency = 23
Retrieve block latency from the simulation.
tDataIn = find(out.logsout.get('validIn').Values.Data == 1); tDataOut = find(out.logsout.get('validOut').Values.Data == 1); actualLatency = tDataOut(1:numSamples) - tDataIn(1:numSamples)
actualLatency = 10×1
23
23
23
23
23
23
23
23
23
23
Ports
Input
Value to take square root of, specified as a non-negative real-valued scalar.
If u is a fixed-point or scaled double data type, u must use binary-point scaling. Slope-bias representation is not supported for fixed-point data types. Only binary-point scaled fixed-point data types are supported for code generation.
Data Types: single | double | fixed point
Whether input is valid, specified as a Boolean scalar. This control signal
indicates when the data from the u input port is valid. When this value
is 1 (true), the block captures the values at
the u input port. When this value is 0
(false), the block ignores input samples.
Data Types: Boolean
Whether to clear internal registers, specified as a Boolean scalar. When this
value is 1 (true), the block stops the current
calculation and clears all internal registers. When this value is 0
(false) and the validIn value is
1 (true), the block begins a new
subframe.
Data Types: Boolean
Output
CORDIC-based approximation of square root of input, returned as a real-valued scalar.
Data Types: single | double | fixed point
Whether output data is valid, returned as a Boolean scalar. This control signal
indicates when the data at the output port y is valid. When this value is
1 (true), the output data is valid. When this
value is 0 (false), the output data is not
valid.
Data Types: Boolean
Parameters
To edit block parameters interactively, use the Property Inspector. From the Simulink® Toolstrip, on the Simulation tab, in the Prepare gallery, select Property Inspector.
Automatically select CORDIC maximum shift value based on input word length. When this parameter is selected, the default CORDIC maximum shift value depends on the word length of the input u:
If the input u is fixed-point or scaled double, the default is the word length minus 1.
If the input u is
single, the default is23.If the input u is
double, the default is52.
Programmatic Use
To set the block parameter value programmatically, use
the set_param function.
To get the block parameter value
programmatically, use the get_param function.
| Parameter: | autoMaximumShiftVal |
| Values: | on (default) | off |
| Data Types: | char | string |
Maximum shift value of hyperbolic vectoring CORDIC, specified as a positive integer-valued scalar.
Dependencies
To enable this parameter, clear the Automatically select CORDIC maximum shift value based on input word length parameter.
Programmatic Use
To set the block parameter value programmatically, use
the set_param function.
To get the block parameter value
programmatically, use the get_param function.
| Parameter: | maximumShiftValue |
| Values: | 10 (default) | positive integer-valued scalar |
| Data Types: | char | string |
Number of CORDIC iterations to perform in pipeline stage, specified as a positive integer-valued scalar. For more information, see Customizable Pipelining.
Programmatic Use
To set the block parameter value programmatically, use
the set_param function.
To get the block parameter value
programmatically, use the get_param function.
| Parameter: | nIterPerReg |
| Values: | 1 (default) | positive integer-valued scalar |
| Data Types: | char | string |
Algorithms
CORDIC is an acronym for COordinate Rotation DIgital Computer. The Givens rotation-based CORDIC algorithm is one of the most hardware-efficient algorithms available because it requires only iterative shift-add operations (see References). The CORDIC algorithm eliminates the need for explicit multipliers. Using CORDIC, you can calculate various functions such as sine, cosine, arcsine, arccosine, arctangent, and vector magnitude. You can also use this algorithm for divide, square root, hyperbolic, and logarithmic functions.
The precision of the CORDIC algorithm is a function of the data type used and the maximum shift value or number of iterations of the CORDIC kernel. Using a data type with a larger word length and performing more iterations of the CORDIC algorithm can reduce the numeric error of the result. However, doing so also increases the latency of the computation and the utilizes more hardware resources. For more information, see How to Set CORDIC Input Word Length and Maximum Shift Value to Achieve Desired Precision.
For details of the CORDIC-based algorithm used in this block, see Compute Square Root Using CORDIC.
Because of its fully pipelined nature, the CORDIC Square Root HDL
Optimized block is able to accept input data on any cycle, including consecutive
clock cycles. To send input data to the block, the validIn signal must be
true. When the block has finished the computation and is ready to send
the output, it will change validOut to true for one clock
cycle. For inputs set on consecutive cycles, validOut will also be set to
true on consecutive cycles.
The latency of the block is defined from the input to the corresponding output. For
example in the figure below, from In1 to Out1,
In2 to Out2, In3 to
Out3, etc.

Use the embblk.latency.cordicSqrtHDLOptimizedLatency function to calculate the latency
of the block and total number of iterations of the block.
The CORDIC Square Root HDL Optimized block uses fully-pipelined
architecture that implements iterative normalization and a CORDIC-based square root
algorithm. If the input u is a fixed-point or scaled double data type, the
block uses multiple pipeline stages for computation. The normalization requires
nextpow2(u.WordLength) iterations. The number of CORDIC iterations
depends on the CORDIC maximum shift
value. A larger word length can provide higher resolution, but requires more
iterations to process. The CORDIC Square Root HDL Optimized block can perform
multiple iterations per pipeline stage. This results in lower latency at the cost of a
longer critical path in the generated HDL code.
For example, if the word length of the input u is 16,
normalization requires 4 iterations. If the Automatically
select CORDIC maximum shift value based on input word length parameter is
selected, the CORDIC maximum shift value is 16 - 1 = 15 and requires
17 iterations. The total number of iterations is 4 + 17 =
21 and the latency of the block is 2 + ceil(total number of
iterations/nIterPerReg). If the number of iterations per pipeline register is
set to 1, then the block latency is 23; if the number
of iterations per pipeline register is set to 2, then the block latency
is 13; etc. If the number of iterations per pipeline register is greater
than the total number of required iterations, the block performs all iterations in one
pipeline stage and the total latency is minimized to 3.
This block supports HDL code generation using the Simulink HDL Workflow Advisor. For an example, see HDL Code Generation and FPGA Synthesis from Simulink Model (HDL Coder) and Implement Digital Downconverter for FPGA (DSP HDL Toolbox).
This example data was generated by synthesizing the block on a Xilinx® Zynq®-7000 xc7z045 SoC. The synthesis tool was Vivado® v2023.1 (win64).
The following synthesis results show the effect of the Number of iterations per pipeline register parameter on the latency and hardware resource utilization.
nIterPerReg = 1These parameters were used for synthesis.
Input data type:
sfix16_en10Automatically select CORDIC maximum shift value based on input word length:
onNumber of iterations per pipeline register:
1Target frequency: 200 MHz
Latency for this configuration: 23
| Resource | Usage | Available | Utilization (%) |
|---|---|---|---|
| Slice LUTs | 966 | 218600 | 0.44 |
| Slice Registers | 670 | 437200 | 0.15 |
| DSPs | 0 | 900 | 0.00 |
| Block RAM Tile | 0 | 545 | 0.00 |
| URAM | 0 | 0 |
Value | |
|---|---|
| Requirement | 5 ns (200 MHz) |
| Data Path Delay | 2.983 ns |
| Slack | 2.01 ns |
| Clock Frequency | 334.45 MHz |
nIterPerReg = 2These parameters were used for synthesis.
Input data type:
sfix16_en10Automatically select CORDIC maximum shift value based on input word length:
onNumber of iterations per pipeline register:
2Target frequency: 200 MHz
Latency for this configuration: 13
| Resource | Usage | Available | Utilization (%) |
|---|---|---|---|
| Slice LUTs | 946 | 218600 | 0.43 |
| Slice Registers | 367 | 437200 | 0.08 |
| DSPs | 0 | 900 | 0.00 |
| Block RAM Tile | 0 | 545 | 0.00 |
| URAM | 0 | 0 |
Value | |
|---|---|
| Requirement | 5 ns (200 MHz) |
| Data Path Delay | 3.677 ns |
| Slack | 1.316 ns |
| Clock Frequency | 271.44 MHz |
nIterPerReg = 3These parameters were used for synthesis.
Input data type:
sfix16_en10Automatically select CORDIC maximum shift value based on input word length:
onNumber of iterations per pipeline register:
3Target frequency: 200 MHz
Latency for this configuration: 9
| Resource | Usage | Available | Utilization (%) |
|---|---|---|---|
| Slice LUTs | 937 | 218600 | 0.43 |
| Slice Registers | 257 | 437200 | 0.06 |
| DSPs | 0 | 900 | 0.00 |
| Block RAM Tile | 0 | 545 | 0.00 |
| URAM | 0 | 0 |
Value | |
|---|---|
| Requirement | 5 ns (200 MHz) |
| Data Path Delay | 3.903 ns |
| Slack | 1.09 ns |
| Clock Frequency | 255.75 MHz |
References
[1] Volder, Jack E. “The CORDIC Trigonometric Computing Technique.” IRE Transactions on Electronic Computers. EC-8, no. 3 (Sept. 1959): 330–334.
[2] Andraka, Ray. “A Survey of CORDIC Algorithm for FPGA Based Computers.” In Proceedings of the 1998 ACM/SIGDA Sixth International Symposium on Field Programmable Gate Arrays, 191–200. https://dl.acm.org/doi/10.1145/275107.275139.
[3] Walther, J.S. “A Unified Algorithm for Elementary Functions.” In Proceedings of the May 18-20, 1971 Spring Joint Computer Conference, 379–386. https://dl.acm.org/doi/10.1145/1478786.1478840.
[4] Schelin, Charles W. “Calculator Function Approximation.” The American Mathematical Monthly, no. 5 (May 1983): 317–325. https://doi.org/10.2307/2975781.
Extended Capabilities
HDL Coder™ provides additional configuration options that affect HDL implementation and synthesized logic.
This block has one default HDL architecture.
| General | |
|---|---|
| ConstrainedOutputPipeline | Number of registers to place at
the outputs by moving existing delays within your design. Distributed
pipelining does not redistribute these registers. The default is
|
| InputPipeline | Number of input pipeline stages
to insert in the generated code. Distributed pipelining and constrained
output pipelining can move these registers. The default is
|
| OutputPipeline | Number of output pipeline stages
to insert in the generated code. Distributed pipelining and constrained
output pipelining can move these registers. The default is
|
Only binary-point scaled fixed-point data types are supported for code generation.
Version History
Introduced in R2024a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
选择网站
选择网站以获取翻译的可用内容,以及查看当地活动和优惠。根据您的位置,我们建议您选择:。
您也可以从以下列表中选择网站:
如何获得最佳网站性能
选择中国网站(中文或英文)以获得最佳网站性能。其他 MathWorks 国家/地区网站并未针对您所在位置的访问进行优化。
美洲
- América Latina (Español)
- Canada (English)
- United States (English)
欧洲
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)
