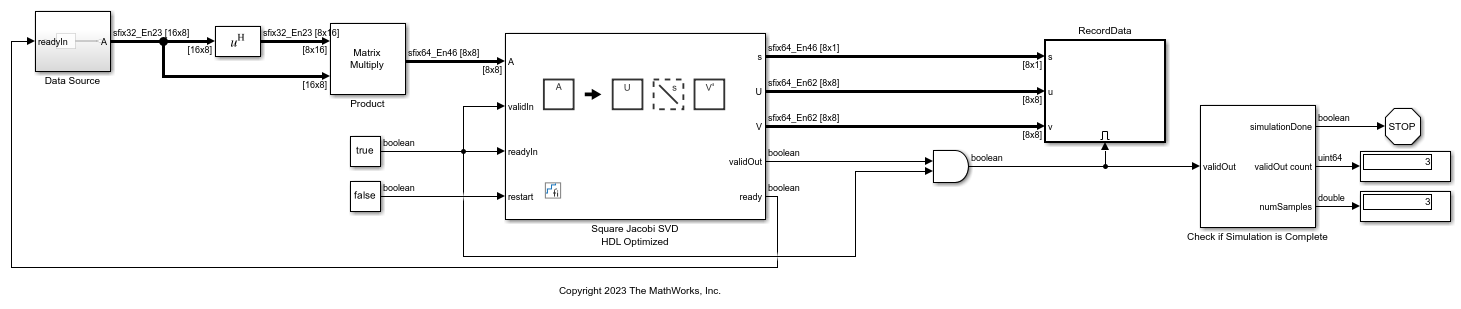
Non-Square Jacobi SVD HDL Optimized

Fixed-point singular value decomposition

Since R2023b

Libraries:
Fixed-Point Designer HDL Support / Matrices and Linear Algebra / Matrix Factorizations

Description

Use the Non-Square Jacobi SVD HDL Optimized block to perform singular value decomposition (SVD) on non-square matrices using QR decomposition and the two-sided Jacobi algorithm. This block consists of a Real Partial-Systolic QR Decomposition or Complex Partial-Systolic QR Decomposition block, depending on your configuration, and a Square Jacobi SVD HDL Optimized. Given a matrix A with more rows than columns, the Non-Square Jacobi SVD HDL Optimized block uses QR decomposition to preprocess the input, then uses the two-sided Jacobi method to produce a vector s of nonnegative elements and unitary matrices U and V such that A = U*diag(s)*V'.

Note

For square matrices, use the Square Jacobi SVD HDL Optimized block.

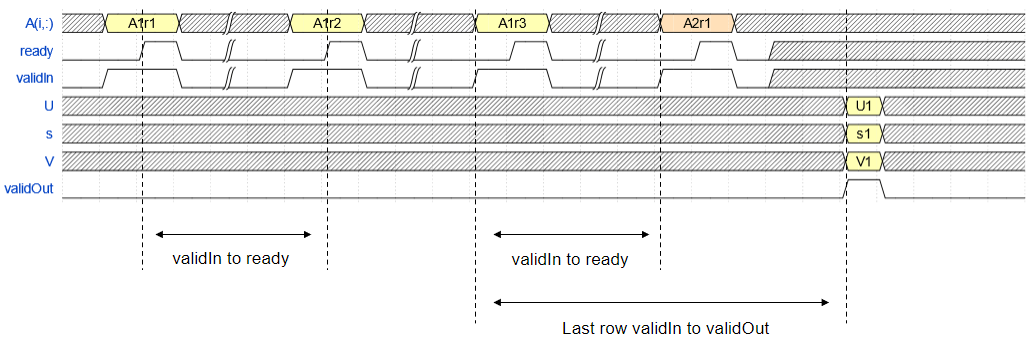
Examples

expand all

How to Use Non-Square Jacobi SVD HDL Optimized Block

Open Live Script

This example shows how to use the Non-Square Jacobi SVD HDL Optimized block to compute the singular value decomposition (SVD) of non-square matrices.

Non-Square Two-Sided Jacobi SVD

The Non-Square Jacobi HDL Optimized block uses the QR decomposition and two-sided Jacobi algorithm to perform singular value decomposition. Given an input matrix A with more rows than columns, the block first uses QR decomposition to preprocess the input, then uses the two-sided Jacobi method to perform singular value decomposition. Because the Jacobi algorithm can perform such computations in parallel, it is suitable for FPGA and ASIC applications. For more information, see Non-Square Jacobi SVD HDL Optimized.

Define Simulation Parameters

Specify the dimension of the sample matrices, the number of input sample matrices, and the number of iterations of the Jacobi algorithm.

m = 16;
n = 8;
rankA = 7;
numSamples = 3;
nIterations = 10;

Generate Input A Matrices

Use the specified simulation parameters to generate the input matrix A.

rng('default');

The Non-Square Jacobi SVD HDL Optimized block supports both real and complex inputs. Set the complexity of the input in the block mask accordingly.

complexity = "real";
A = zeros(m,n,numSamples);
for k = 1:numSamples
    switch complexity
        case 'complex'
            A(:,:,k) = fixed.example.complexRandomLowRankMatrix(m,n,rankA);
        case 'real'
            A(:,:,k) = fixed.example.realRandomLowRankMatrix(m,n,rankA);
        otherwise
            error("Complexity must be either 'real' or 'complex'")
    end
end

Select Fixed-Point Data Types

Define the desired word length.

wordLength = 25;

Use the upper bound on the singular values to define fixed-point types that will never overflow. First, use the fixed.singularValueUpperBound function to determine the upper bound on the singular values.

svdUpperBound = fixed.singularValueUpperBound(m,n,max(abs(A(:))));

Define the integer length based on the value of the upper bound, with one additional bit for the sign, another additional bit for intermediate CORDIC growth, and one more bit for intermediate growth to compute the Jacobi rotations.

additionalBitGrowth = 3;
integerLength = ceil(log2(svdUpperBound)) + additionalBitGrowth;

Compute the fraction length based on the integer length and the desired word length.

fractionLength = wordLength - integerLength;

Define the signed fixed-point data type to be 'Fixed' or 'ScaledDouble'. You can also define the type to be 'double' or 'single'.

dataType = 'Fixed';
T.A = fi([],1,wordLength,fractionLength,'DataType',dataType);
disp(T.A)

[]

          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 25
        FractionLength: 18

Cast the matrix A to the signed fixed-point type.

A = cast(A,'like',T.A);

Configure Model Workspace and Run Simulation

model = 'NonSquareJacobiSVDModel';
load_system(model);
open_system(model);

Set the parameter for real or complex either using set_param, or from the dialog.

set_param('NonSquareJacobiSVDModel/Non-Square Jacobi SVD HDL Optimized','complexity',complexity);

Set the variables in the model workspace.

fixed.example.setModelWorkspace(model,'A',A,'m',m,'n',n,...
    'nIterations',nIterations,'numSamples',numSamples);
out = sim(model);

Verify Output Solutions

Verify the output solutions. In these steps, "identical" means within roundoff error.

Verify that U*diag(s)*V' is identical to A. relativeErrorUSV represents the relative error between U*diag(s)*V' and A.
Verify that the singular values s are identical to the floating-point SVD solution. relativeErrorS represents the relative error between s and the singular values calculated by the MATLAB® svd function.
Verify that U and V are unitary matrices. relativeErrorUU represents the relative error between U'*U and the identity matrix. relativeErrorVV represents the relative error between V'*V and the identity matrix.

for i = 1:numSamples
    disp(['Sample #',num2str(i),':']);
    a = A(:,:,i);
    U = out.U(:,:,i);
    V = out.V(:,:,i);
    s = out.s(:,:,i);

    % Verify U*diag(s)*V'
    if norm(double(a)) > 1
        relativeErrorUSV = norm(double(U*diag(s)*V')-double(a))/norm(double(a));
    else
        relativeErrorUSV = norm(double(U*diag(s)*V')-double(a)); 
    end    
    relativeErrorUSV
    
    % Verify s
    s_expected = svd(double(a));
    normS = norm(s_expected);
    relativeErrorS = norm(double(s) - s_expected);
    if normS > 1
        relativeErrorS = relativeErrorS/normS;
    end
    relativeErrorS

    % Verify U'*U
    % U'*U will only be unitary up to the rank of A
    U = double(U);
    UU = U(:,1:rankA)'*U(:,1:rankA);
    relativeErrorUU = norm(UU - eye(size(UU)))
    
    % Verify V'*V
    V = double(V);
    VV = V'*V;
    relativeErrorVV = norm(VV - eye(size(VV)))

    disp('---------------');
end

Sample #1:

relativeErrorUSV = 
2.3251e-04

relativeErrorS = 
9.8161e-05

relativeErrorUU = 
3.5827e-05

relativeErrorVV = 
3.7335e-05

---------------

Sample #2:

relativeErrorUSV = 
3.3725e-04

relativeErrorS = 
6.5314e-05

relativeErrorUU = 
2.4210e-05

relativeErrorVV = 
3.5644e-05

---------------

Sample #3:

relativeErrorUSV = 
4.5802e-04

relativeErrorS = 
1.2924e-04

relativeErrorUU = 
4.2547e-05

relativeErrorVV = 
3.5511e-05

---------------

Extended Examples

Implement HDL Optimized SVD for Non-Square Matrix with Scalar Input and Simplified AXI4 Protocol

Use the Non-Square Jacobi SVD HDL Optimized block to compute the singular value decomposition (SVD) of non-square matrices. The input data is in scalar format and uses simplified AXI4 protocol. The Non-Square Jacobi SVD HDL Optimized block uses the AMBA AXI handshake protocol for both input and output. The valid/ready handshake process is used to transfer data and control information. For more details about the handshake process, see Non-Square Jacobi SVD HDL Optimized. In certain use cases such as using this block with IP core generation workflow, this block needs to interface with upstream block using the Model Design for AXI4-Stream Interface Generation (HDL Coder). In this example, the sAXI2AXI block serves as an adapter between simplified AXI and AMBA AXI protocols. It also converts the scalar input into row format and feeds into the Non-Square Jacobi SVD HDL Optimized block.

Open Script

Compute SVD of Non-Square Matrices Using Square Jacobi SVD HDL Optimized Block by Forming Covariance Matrices

Use the Square Jacobi SVD HDL Optimized block to compute the singular value decomposition (SVD) of non-square matrices by forming covariance matrices.

Open Script

Limitations

To optimize HDL efficiency, if the input matrix A is not full rank, then the output U matrix is orthonormal up to the rank of A. $A = U * d i a g (s) * V'$ is still valid. V is always orthonormal regardless of the rank of A.

For example, if $A = [\begin{matrix} 1 & 1 & 1 \\ 2 & 2 & 2 \\ 3 & 3 & 3 \\ 0.5 & 2 & 4 \end{matrix}]$ , then A has rank 2 and $U' * U = [\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0.8940 \end{matrix}]$ .

If the input matrix is full rank, then $U' * U = I$ , where I = eye(n).

Ports

Input

expand all

A(i,:) — Rows of matrix A
vector

Row of matrix A, specified as a vector. A is a m-by-n matrix where m > 2, n ≥ 2, and m > n.

If A is a fixed-point data type, A must be signed and use binary-point scaling. Slope-bias representation is not supported for fixed-point data types.

Tips

The output U matrix is orthonormal up to the rank of input matrix A. For more information, see Limitations.

Data Types: single | double | fixed point
Complex Number Support: Yes

validIn — Whether input is valid
scalar

Whether input is valid, specified as a Boolean scalar. This control signal indicates when the data from the A input port is valid. When this value is 1 (true) and the value at ready is 1 (true), the block captures the values at the A input port. When this value is 0 (false), the block ignores the input samples.

Tips

After sending a true validIn signal, a delay may occur before the ready signal is false. To ensure all data is processed, you must wait until the ready signal is false before sending another true validIn signal.

Data Types: Boolean

readyIn — Whether downstream block is ready
scalar

Whether downstream block is ready, specified as a Boolean scalar. This control signal monitors the ready port of the downstream block. When the readyIn value is 1 (true), and the value at validOut is 1 (true), the block outputs data to the downstream block. When the readyIn value is 0 (false), the downstream block is not ready to accept data. The Non-Square Jacobi SVD HDL Optimized block pauses on the output stage and the ready signal remains 0 (false) until the readyIn signal is high.

Data Types: Boolean

restart — Whether to clear internal states
scalar

Whether to clear internal states, specified as a Boolean scalar. When this value is 1 (true), the block stops the current calculation and clears all internal states. When this value is 0 (false) and the validIn value is 1 (true), the block begins a new subframe.

Data Types: Boolean

Output

expand all

s — Singular values
column vector

Singular values, returned as a column vector of length n. The Singular Values are nonnegative and returned in descending order such that s(1) >= s(2) >= ... >= s(n). Singular values are returned with the same data type as the input matrix A.

Data Types: single | double | fixed point

U — Left singular vectors
unitary `n`-by-`n` matrix

Left singular vectors, returned as a unitary n-by-n matrix.

For fixed-point and scaled-double inputs, U is returned as a signed fixed-point or scaled-double fi with the same word length as A and fraction length equal to two less than the word length. One of these integer bits is used for the sign. The other integer bit allows +1 to be represented exactly.

For floating-point input, U has the same data type as A.

Tips

The output U matrix is orthonormal up to the rank of input matrix A. For more information, see Limitations.

Dependencies

To enable this port, set the Select outputs parameter to UsV or Us.

Data Types: single | double | fixed point

V — Right singular vectors
unitary `n`-by-`n` matrix

Right singular vectors, returned as a unitary n-by-n matrix.

For fixed-point and scaled-double inputs, V is returned as a signed fixed-point or scaled-double fi with the same word length as A and fraction length equal to two less than the word length. One of these integer bits is used for the sign. The other integer bit allows +1 to be represented exactly.

For floating-point input, V has the same data type as A.

Dependencies

To enable this port, set the Select outputs parameter to UsV or sV.

Data Types: single | double | fixed point

validOut — Whether output data is valid
`Boolean` scalar

Whether the output data is valid, returned as a Boolean scalar. This control signal indicates when the data at the output ports U, S, and V are valid. When this value is 1 (true), the output data is valid. When this value is 0 (false), the output data is not valid. Transfer of data to the downstream block occurs only when both the validOut and readyIn signals are high.

Data Types: Boolean

ready — Whether block is ready
`Boolean` scalar

Whether the block is ready, returned as a Boolean scalar. This control signal indicates when the block is ready for new input data. When this value is 1 (true) and the validIn value is 1 (true), the block accepts input data in the next time step. When this value is 0 (false), the block ignores input data in the next time step.

Tips

After sending a true validIn signal, there may be some delay before the ready signal is false. To ensure all data is processed, you must wait until the ready signal is false before sending another true validIn signal.

Data Types: Boolean

Parameters

expand all

To edit block parameters interactively, use the Property Inspector. From the Simulink^® Toolstrip, on the Simulation tab, in the Prepare gallery, select Property Inspector.

Number of rows in matrix A — Number of rows in m-by-n matrix A
`8` (default) | integer-valued scalar where `m > 2` and `m > n`

Number of rows in m-by-n matrix A, specified as an integer-valued scalar where m > 2 and m > n.

Programmatic Use

To set the block parameter value programmatically, use the set_param function.

To get the block parameter value programmatically, use the get_param function.

Parameter:	`m`
Values:	8 (default) \| integer-valued scalar where `m > 2` and `m > n`
Data Types:	`char` \| `string`

Number of columns in matrix A — Number of columns in m-by-n matrix A
`4` (default) | integer-valued scalar where `n ≥ 2` and `m > n`

Number of columns in m-by-n matrix A, specified as an integer-valued scalar where n ≥ 2 and m > n.

Programmatic Use

To set the block parameter value programmatically, use the set_param function.

To get the block parameter value programmatically, use the get_param function.

Parameter:	`n`
Values:	4 (default) \| integer-valued scalar where `n ≥ 2` and `m > n`
Data Types:	`char` \| `string`

Number of Jacobi iterations — Number of iterations of Jacobi algorithm
`10` (default) | positive integer

Number of iterations of the Jacobi algorithm, specified as a positive integer.

Tips

Most sources indicate that 10 iterations is sufficient for the Jacobi algorithm to converge [7][8][9][10].
When the input is an m-by-2 matrix, the SVD has a closed-form solution and does not require iterative computation. In this case, set the Number of Jacobi iterations to 1 to minimize utilization and latency.

Programmatic Use

To set the block parameter value programmatically, use the set_param function.

To get the block parameter value programmatically, use the get_param function.

Parameter:	`nIterations`
Values:	`10` (default) \| positive integer
Data Types:	`char` \| `string`

Select outputs — Block outputs
`UsV` (default) | `Us` | `sV` | `s`

Block outputs, specified as UsV, Us, sV, or s.

Tips

This parameter determines the number of outputs on the block.

Programmatic Use

To set the block parameter value programmatically, use the set_param function.

To get the block parameter value programmatically, use the get_param function.

Parameter:	`outputOption`
Values:	`UsV` (default) \| `Us` \| `sV` \| `s`
Data Types:	`char` \| `string`

Signal type — Complexity of input matrix A
`real` (default) | `complex`

Complexity of the input matrix A, specified as real, or complex.

Tips

This parameter determines whether the Non-Square Jacobi HDL Optimized block uses a Real Partial-Systolic QR Decomposition block or a Complex Partial-Systolic QR Decomposition block to preprocess the input.

Programmatic Use

To set the block parameter value programmatically, use the set_param function.

To get the block parameter value programmatically, use the get_param function.

Parameter:	`complexity`
Values:	`real` (default) \| `complex`
Data Types:	`char` \| `string`

Tips

The behavior of the Non-Square Jacobi SVD HDL Optimized block is equivalent to [U,s,V] = fixed.jacobiSVD(A) when A is a non-square matrix. If the input data type is fixed point with binary-point scaling, the function and the block provide bit-exact results. However, if the input data type is floating point, small numerical differences may exist between the function and the block.
The Number of Jacobi iterations block parameter is equivalent to the numberOfSweeps input argument for the fixed.jacobiSVD function.

Algorithms

expand all

Jacobi Singular Value Decomposition

The Non-Square Jacobi SVD HDL Optimized block uses QR decomposition and a two-sided Jacobi algorithm for singular value decomposition (SVD) [2][3][4]. Compared to the sequential Golub-Kahan-Reinsch algorithm for SVD [5], the Jacobi algorithm has inherent parallelism and performs better for FPGA and ASIC applications [6]. The Jacobi method is an iterative algorithm. Use the Number of Jacobi iterations parameter to set the number of iterations necessary for convergence. Most sources indicate that 10 iterations is sufficient for the Jacobi algorithm to converge [7][8][9][10].

AMBA AXI Handshake Process

This block uses the AMBA AXI handshake protocol on both the input and the output side [1]. The valid/ready handshake process is used to transfer data and control information. This two-way control mechanism allows both the manager and subordinate to control the rate at which information moves between manager and subordinate.

On the input side, the validIn signal indicates when the upstream data is available. The ready signal indicates that the block can accept the data. Transfer of data from the upstream block occurs only when both the validIn and ready signals are high.

On the output side, the validOut signal indicates the solution data is available. The readyIn signal indicates when the downstream block can accept data. Transfer of data to the downstream block occurs only when both the validOut and readyIn signals are high.

When the readyIn signal is low, the block pauses on the output stage and the ready signal remains low. This configuration allows a stall from the downstream block to back-propagate to the upstream block.

To use the Non-Square Jacobi SVD HDL Optimized block in feed-forward fashion without back pressure from the downstream block, feed a constant Boolean 'true' to the readyIn port.

Block Timing

The Non-Square Jacobi SVD HDL Optimized block accepts the matrix A row by row. After accepting m rows, the block outputs U, s, and V.

For example, assume that validIn asserts before ready, meaning that the upstream data source is faster than the Non-Square Jacobi SVD HDL Optimized block. Additionally, assume that readyIn is always asserted, meaning that the downstream consumer of the data is faster than the Square Jacobi SVD HDL Optimized.

In the figure:

A1r1 is the first row of the first A matrix, s1 is the first s vector, and so on.
validIn to ready — From a successful row input to the block being ready to accept the next row.
Last row validIn to validOut — From the last row input to the block starting to output the solution.

The latency of the Non-Square Jacobi SVD HDL Optimized block depends on the size (m, n), complexity, and word length (wl) of the input matrix A, the number of iterations (nIterations) of the two-sided Jacobi algorithm, and whether the output U is selected, as summarized in the tables.

If the data type of A is fixed point, then wl is the word length.
If the data type of A is double precision, then wl is 53.
If the data type of A is single precision, then wl is 24.

Signal type (`complexity`)	Select outputs (`outputOption`)	`validIn` to `ready`
`real`	`UsV` or `Us`	max([wl+7,ceil(((wl2+31)(n-1+rem(n,2))... nIterations+2+nextpow2(n)... (nextpow2(n)+1)/2+3+2)/m),... ceil((m*n+1)/m)])
`real`	`sV` or `s`	max([wl+7,ceil(((wl2+31)(n-1+rem(n,2))... nIterations+2+nextpow2(n)... (nextpow2(n)+1)/2+3+2)/m)])
`complex`	`UsV` or `Us`	max([wl+9,ceil(((wl6+48)(n-1+rem(n,2))... nIterations+2+nextpow2(n)... (nextpow2(n)+1)/2+3+2)/m),... ceil((m*n+1)/m)])
`complex`	`sV` or `s`	max([wl+9,ceil(((wl6+48)(n-1+rem(n,2))... nIterations+2+nextpow2(n)... (nextpow2(n)+1)/2+3+2)/m])

Signal type (`complexity`)	Select outputs (`outputOption`)	Last row `validIn` to `validOut`
`real`	`UsV` or `Us`	((wl+6)n)+6+2+(wl2+31)(n-1+rem(n,2))... nIterations+2+nextpow2(n)... (nextpow2(n)+1)/2+3+mn+1
`real`	`sV` or `s`	((wl+6)n)+6+2+(wl2+31)... (n-1+rem(n,2))nIterations... +2+nextpow2(n)*(nextpow2(n)+1)/2+3
`complex`	`UsV` or `Us`	((wl+7.5)2n)+6+2+(wl6+48)(n-1+rem(n,2))... nIterations+2+nextpow2(n)... (nextpow2(n)+1)/2+3+m*n+1
`complex`	`sV` or `s`	((wl+7.5)2n)+6+2+(wl6+48)(n-1+rem(n,2))... nIterations+2+nextpow2(n)... (nextpow2(n)+1)/2+3

Hardware Resource Utilization

This block supports HDL code generation using the Simulink HDL Workflow Advisor. For an example, see HDL Code Generation and FPGA Synthesis from Simulink Model (HDL Coder) and Implement Digital Downconverter for FPGA (DSP HDL Toolbox).

This example data was generated by synthesizing the block on a Xilinx^® Zynq^® UltraScale+™ RFSoC ZCU111 evaluation board. The synthesis tool was Vivado^® v2022.1 (win64).

Signal Type: Real

The following parameters were used for synthesis.

Block parameters:
- n = 8
- nIterations = 10
Input data type: sfix16_En12
Target frequency: 100 MHz

The following tables show the post place-and-route resource utilization results and timing summary, respectively.

Resource	Usage	Available	Utilization
CLB LUTs	1.0238e+05	425280	24.07
CLB Registers	82768	850560	9.73
DSPs	72	4272	1.69
Block RAM Tile	0	1080	0
URAM	0	80	0

	Value
Requirement	10 ns (100 MHz)
Data Path Delay	8.739 ns
Slack	1.243 ns
Clock Frequency	114.19 MHz

Signal Type: Complex

The following parameters were used for synthesis.

Block parameters:
- n = 8
- nIterations = 10
Input data type: sfix16_En12
Target frequency: 100 MHz

These tables show the post place-and-route resource utilization results and timing summary, respectively.

Resource	Usage	Available	Utilization
CLB LUTs	2.8337e+05	425280	66.63
CLB Registers	2.2146e+05	850560	26.04
DSPs	368	4272	8.61
Block RAM Tile	0	1080	0
URAM	0	80	0

	Value
Requirement	10 ns (100 MHz)
Data Path Delay	9.481 ns
Slack	0.499 ns
Clock Frequency	105.25 MHz

References

[1] Arm Developer. "AMBA AXI and ACE Protocol Specification Version E." https://developer.arm.com/documentation/ihi0022/e/AMBA-AXI3-and-AXI4-Protocol-Specification/Single-Interface-Requirements/Basic-read-and-write-transactions/Handshake-process.

[2] Jacobi, Carl G. J., "Über ein leichtes Verfahren die in der Theorie der Säcularstörungen vorkommenden Gleichungen numerisch aufzulösen." Journal fur die reine und angewandte Mathematik 30 (1846): 51–94.

[3] Forsythe, George E. and Peter Henrici. "The Cyclic Jacobi Method for Computing the Principal Values of a Complex Matrix." Transactions of the American Mathematical Society 94, no. 1 (January 1960): 1-23.

[4] Shiri, Aidin and Ghader Khosroshahi. "An FPGA Implementation of Singular Value Decomposition", ICEE 2019: 27th Iranian Conference on Electrical Engineering, Yazd, Iran, April 30–May 2, 2019, 416-22, IEEE.

[5] Golub, Gene H. and Charles F. Van Loan. Matrix Computations, 4th ed. Baltimore, MD: Johns Hopkins University Press, 2013.

[6] Athi, Mrudula V., Seyed R. Zekavat, and Alan A. Struthers. "Real-Time Signal Processing of Massive Sensor Arrays via a Parallel Fast Converging SVD Algorithm: Latency, Throughput, and Resource Analysis." IEEE Sensors Journal 16, no. 18 (January 2016): 2519-26. https://doi.org/10.1109/JSEN.2016.2517040.

[7] Brent, Richard P., Franklin T. Luk, and Charles Van Loan. "Computation of the Singular Value Decomposition Using Mesh-Connected Processors." Journal of VLSI and Computer Systems 1, 3 (1985): 242–70.

[8] Hemkumar, Nariankadu D. A Systolic VLSI Architecture for Complex SVD. Master’s thesis, Rice University, 1991.

[9] Duryea, R. A. Finite Precision Arithmetic in Singular Value Decomposition Architectures. Ph.D. thesis, Cornell University, 1987.

[10] Cavallaro, Joseph R. and Franklin T. Luk. 1987. "CORDIC Arithmetic for an SVD Processor." 1987 IEEE 8th Symposium on Computer Arithmetic (ARITH), Como, Italy, May 18-21, 1987, 113-20. IEEE. https://doi.org/10.1109/ARITH.1987.6158686.

Extended Capabilities

HDL Code Generation
Generate VHDL, Verilog and SystemVerilog code for FPGA and ASIC designs using HDL Coder™.

Note

When generating code for large matrices set the configuration parameter HDL Code Generation > Global Settings > Ports tab Check for DUT pin count exceeding I/O Threshold to Warning or None. To learn more about this setting, see Check for DUT pin count exceeding I/O Threshold (HDL Coder).

HDL Coder™ provides additional configuration options that affect HDL implementation and synthesized logic.

HDL Architecture

This block has one default HDL architecture.

HDL Block Properties

General
ConstrainedOutputPipeline	Number of registers to place at the outputs by moving existing delays within your design. Distributed pipelining does not redistribute these registers. The default is `0`. For more details, see ConstrainedOutputPipeline (HDL Coder).
InputPipeline	Number of input pipeline stages to insert in the generated code. Distributed pipelining and constrained output pipelining can move these registers. The default is `0`. For more details, see InputPipeline (HDL Coder).
OutputPipeline	Number of output pipeline stages to insert in the generated code. Distributed pipelining and constrained output pipelining can move these registers. The default is `0`. For more details, see OutputPipeline (HDL Coder).

Restrictions

Supports fixed-point data types only. Fixed-point data types must use signed binary-point scaling. Slope and bias scaling and unsigned fixed-point types are not supported.

Version History

Introduced in R2023b

Non-Square Jacobi SVD HDL Optimized

Description

Examples

How to Use Non-Square Jacobi SVD HDL Optimized Block

Extended Examples

Implement HDL Optimized SVD for Non-Square Matrix with Scalar Input and Simplified AXI4 Protocol

Compute SVD of Non-Square Matrices Using Square Jacobi SVD HDL Optimized Block by Forming Covariance Matrices

Limitations

Ports

Input

A(i,:) — Rows of matrix A vector

Tips

validIn — Whether input is valid scalar

Tips

readyIn — Whether downstream block is ready scalar

restart — Whether to clear internal states scalar

Output

s — Singular values column vector

U — Left singular vectors unitary n-by-n matrix

Tips

Dependencies

V — Right singular vectors unitary n-by-n matrix

Dependencies

validOut — Whether output data is valid Boolean scalar

ready — Whether block is ready Boolean scalar

Tips

Parameters

Number of rows in matrix A — Number of rows in m-by-n matrix A 8 (default) | integer-valued scalar where m > 2 and m > n

Programmatic Use

Number of columns in matrix A — Number of columns in m-by-n matrix A 4 (default) | integer-valued scalar where n ≥ 2 and m > n

Programmatic Use

Number of Jacobi iterations — Number of iterations of Jacobi algorithm 10 (default) | positive integer

Tips

Programmatic Use

Select outputs — Block outputs UsV (default) | Us | sV | s

Tips

Programmatic Use

Signal type — Complexity of input matrix A real (default) | complex

Tips

Programmatic Use

Tips

Algorithms

Jacobi Singular Value Decomposition

AMBA AXI Handshake Process

Block Timing

Hardware Resource Utilization

References

Extended Capabilities

HDL Code Generation Generate VHDL, Verilog and SystemVerilog code for FPGA and ASIC designs using HDL Coder™.

Version History

See Also

Blocks

Functions

A(i,:) — Rows of matrix A
vector

validIn — Whether input is valid
scalar

readyIn — Whether downstream block is ready
scalar

restart — Whether to clear internal states
scalar

s — Singular values
column vector

U — Left singular vectors
unitary `n`-by-`n` matrix

V — Right singular vectors
unitary `n`-by-`n` matrix

validOut — Whether output data is valid
`Boolean` scalar

ready — Whether block is ready
`Boolean` scalar

Number of rows in matrix A — Number of rows in m-by-n matrix A
`8` (default) | integer-valued scalar where `m > 2` and `m > n`

Number of columns in matrix A — Number of columns in m-by-n matrix A
`4` (default) | integer-valued scalar where `n ≥ 2` and `m > n`

Number of Jacobi iterations — Number of iterations of Jacobi algorithm
`10` (default) | positive integer

Select outputs — Block outputs
`UsV` (default) | `Us` | `sV` | `s`

Signal type — Complexity of input matrix A
`real` (default) | `complex`

HDL Code Generation
Generate VHDL, Verilog and SystemVerilog code for FPGA and ASIC designs using HDL Coder™.