Singular Values

A singular value and corresponding singular vectors of a rectangular matrix A are, respectively, a scalar σ and a pair of vectors u and v that satisfy

$\begin{array}{l} A v = σ u \\ A^{H} u = σ v, \end{array}$

where $A^{H}$ is the Hermitian transpose of A. The singular vectors u and v are typically scaled to have a norm of 1. Also, if u and v are singular vectors of A, then -u and -v are singular vectors of A as well.

The singular values σ are always real and nonnegative, even if A is complex. With the singular values in a diagonal matrix Σ and the corresponding singular vectors forming the columns of two orthogonal matrices U and V, you obtain the equations

$\begin{array}{l} A V = U Σ \\ A^{H} U = V Σ . \end{array}$

Since U and V are unitary matrices, multiplying the first equation by $V^{H}$ on the right yields the singular value decomposition equation

$A = U Σ V^{H} .$

The full singular value decomposition of an m-by-n matrix involves:

m-by-m matrix U
m-by-n matrix Σ
n-by-n matrix V

In other words, U and V are both square, and Σ is the same size as A. If A has many more rows than columns (m > n), then the resulting m-by-m matrix U is large. However, most of the columns in U are multiplied by zeros in Σ. In this situation, the economy-sized decomposition saves both time and storage by producing an m-by-n U, an n-by-n Σ and the same V:

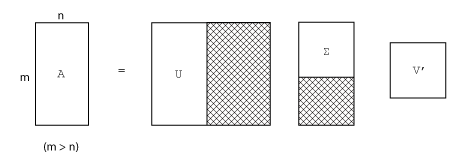
In the economy-sized decomposition, columns in U can be ignored if they multiply zeros in the diagonal matrix of singular values.

The eigenvalue decomposition is the appropriate tool for analyzing a matrix when it represents a mapping from a vector space into itself, as it does for an ordinary differential equation. However, the singular value decomposition is the appropriate tool for analyzing a mapping from one vector space into another vector space, possibly with a different dimension. Most systems of simultaneous linear equations fall into this second category.

If A is square, symmetric, and positive definite, then its eigenvalue and singular value decompositions are the same. But, as A departs from symmetry and positive definiteness, the difference between the two decompositions increases. In particular, the singular value decomposition of a real matrix is always real, but the eigenvalue decomposition of a real, nonsymmetric matrix might be complex.

For the example matrix

A = [9     4
     6     8
     2     7];

the full singular value decomposition is

[U,S,V] = svd(A)

U =

   -0.6105    0.7174    0.3355
   -0.6646   -0.2336   -0.7098
   -0.4308   -0.6563    0.6194


S =

   14.9359         0
         0    5.1883
         0         0


V =

   -0.6925    0.7214
   -0.7214   -0.6925

You can verify that U*S*V' is equal to A to within round-off error. For this small problem, the economy size decomposition is only slightly smaller.

[U,S,V] = svd(A,"econ")

U =

   -0.6105    0.7174
   -0.6646   -0.2336
   -0.4308   -0.6563


S =

   14.9359         0
         0    5.1883


V =

   -0.6925    0.7214
   -0.7214   -0.6925

Again, U*S*V' is equal to A to within round-off error.

Batched SVD Calculation

If you need to decompose a large collection of matrices that have the same size, it is inefficient to perform all of the decompositions in a loop with svd. Instead, you can concatenate all of the matrices into a multidimensional array and use pagesvd to perform singular value decompositions on all of the array pages with a single function call.

Function	Usage
`pagesvd`	Use `pagesvd` to perform singular value decompositions on the pages of a multidimensional array. This is an efficient way to perform SVD on a large collection of matrices that all have the same size.

For example, consider a collection of three 2-by-2 matrices. Concatenate the matrices into a 2-by-2-by-3 array with the cat function.

A = [0 -1; 1 0];
B = [-1 0; 0 -1];
C = [0 1; -1 0];
X = cat(3,A,B,C);

Now, use pagesvd to simultaneously perform the three decompositions.

[U,S,V] = pagesvd(X);

For each page of X, there are corresponding pages in the outputs U, S, and V. For example, the matrix A is on the first page of X, and its decomposition is given by U(:,:,1)*S(:,:,1)*V(:,:,1)'.

Low-Rank SVD Approximations

For large sparse matrices, using svd to calculate all of the singular values and singular vectors is not always practical. For example, if you need to know just a few of the largest singular values, then calculating all of the singular values of a 5000-by-5000 sparse matrix is extra work.

In cases where only a subset of the singular values and singular vectors are required, the svds and svdsketch functions are preferred over svd.

Function	Usage
`svds`	Use `svds` to calculate a rank-k approximation of the SVD. You can specify whether the subset of singular values should be the largest, the smallest, or the closest to a specific number. `svds` generally calculates the best possible rank-k approximation.
`svdsketch`	Use `svdsketch` to calculate a partial SVD of the input matrix satisfying a specified tolerance. While `svds` requires that you specify the rank, `svdsketch` adaptively determines the rank of the matrix sketch based on the specified tolerance. The rank-k approximation that `svdsketch` ultimately uses satisfies the tolerance, but unlike `svds`, it is not guaranteed to be the best one possible.

For example, consider a 1000-by-1000 random sparse matrix with a density of about 30%.

n = 1000;
A = sprand(n,n,0.3);

The six largest singular values are

S = svds(A)

S =

  130.2184
   16.4358
   16.4119
   16.3688
   16.3242
   16.2838

Also, the six smallest singular values are

S = svds(A,6,"smallest")

S =

    0.0740
    0.0574
    0.0388
    0.0282
    0.0131
    0.0066

For smaller matrices that can fit in memory as a full matrix, full(A), using svd(full(A)) might still be quicker than svds or svdsketch. However, for truly large and sparse matrices, using svds or svdsketch becomes necessary.

Singular Values

Batched SVD Calculation

Low-Rank SVD Approximations

See Also

Related Topics