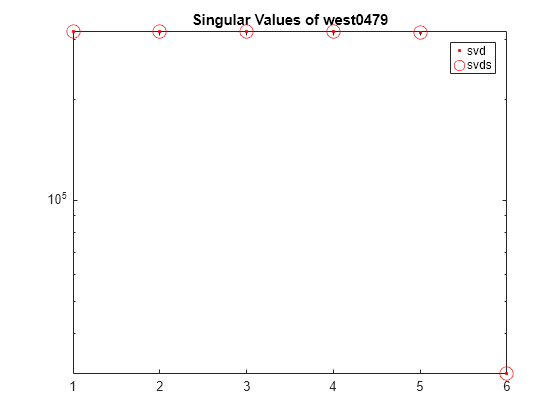
svds

奇异值和向量的子集

全页折叠

语法

s = svds(A)

s = svds(A,k)

s = svds(A,k,sigma)

s = svds(A,k,sigma,Name,Value)

s = svds(A,k,sigma,opts)

s = svds(Afun,n,___)

[U,S,V] = svds(___)

[U,S,V,flag] = svds(___)

说明

s = svds(A) 返回一个向量，其中包含矩阵 A 的六个最大的奇异值。当使用 svd 计算所有奇异值的计算量很大时（例如对于大型稀疏矩阵而言），可以使用此函数。

示例

s = svds(A,k) 返回 k 个最大奇异值。

示例

s = svds(A,k,sigma) 基于 sigma 的值返回 k 个奇异值。例如，svds(A,k,'smallest') 返回 k 个最小奇异值。

示例

s = svds(A,k,sigma,Name,Value) 使用一个或多个名称-值对组参量指定其他选项。例如，svds(A,k,sigma,'Tolerance',1e-3) 将调整算法的收敛容差。

s = svds(A,k,sigma,opts) 使用结构体指定选项。

示例

s = svds(Afun,n,___) 指定函数句柄 Afun，而不是矩阵。第二个输入 n 可求出 Afun 中使用的矩阵 A 的大小。您可以选择指定 k、sigma、opts 或名称-值对组作为额外的输入参量。

示例

[U,S,V] = svds(___) 返回左奇异向量 U、奇异值的对角矩阵 S 以及右奇异向量 V。您可以使用上述语法中的任何输入参量组合。

示例

[U,S,V,flag] = svds(___) 也返回一个收敛标志。如果 flag 为 0，则表示所有奇异值已收敛。

示例

全部折叠

最大奇异值

打开实时脚本

矩阵 A = delsq(numgrid('C',15)) 是一个对称正定矩阵，奇异值合理分布在区间 (0 8) 中。计算六个最大的奇异值。

A = delsq(numgrid('C',15));
s = svds(A)

指定第二个输入，以计算特定数量的最大奇异值。

s = svds(A,3)

最小奇异值

打开实时脚本

矩阵 A = delsq(numgrid('C',15)) 是一个对称正定矩阵，奇异值合理分布在区间 (0 8) 中。计算五个最小的奇异值。

A = delsq(numgrid('C',15));
s = svds(A,5,'smallest')

最小非零奇异值

打开实时脚本

创建一个 100×100 的稀疏纽曼矩阵。

C = gallery('neumann',100);

计算十个最小的奇异值。

ss = svds(C,10,'smallest')

计算十个最小的非零奇异值。由于该矩阵有一个奇异值等于零，因此 'smallestnz' 选项将忽略它。

snz = svds(C,10,'smallestnz')

使用函数句柄的最大奇异值

打开脚本

创建两个矩阵，表示稀疏矩阵右上角和左下角的非零块。

n = 500;
B = rand(500);
C = rand(500);

将 Afun 保存到您的当前目录中，以便其可用于 svds。

function y = Afun(x,tflag,B,C,n)
if strcmp(tflag,'notransp')
    y = [B*x(n+1:end); C*x(1:n)];
else
    y = [C'*x(n+1:end); B'*x(1:n)];
end

函数 Afun 使用 B 和 C 来计算 A*x 或 A'*x（具体取决于指定的标志），而不用真正建立整个稀疏矩阵 A = [zeros(n) B; C zeros(n)]。这种方法可以在计算 A*x 和 A'*x 时充分利用矩阵的稀疏模式来节省内存。

使用 Afun 计算 A 的 10 个最大的奇异值。将 B、C 和 n 作为额外输入传递给 Afun。

s = svds(@(x,tflag) Afun(x,tflag,B,C,n),[1000 1000],10)

直接计算 A 的 10 个最大的奇异值以比较结果。

A = [zeros(n) B; C zeros(n)];
s = svds(A,10)

稀疏矩阵的奇异值分解

打开实时脚本

west0479 是一个 479×479 的实数值稀疏矩阵。该矩阵有几个较大的奇异值和许多较小的奇异值。

加载 west0479 并将其存储为 A。

load west0479
A = west0479;

计算 A 的奇异值分解，返回六个最大的奇异值和对应的奇异向量。指定第四个输出参量，以检查奇异值的收敛。

[U,S,V,cflag] = svds(A);
cflag

cflag = 
0

cflag 表示所有奇异值已收敛。奇异值位于输出矩阵 S 的对角线上。

s = diag(S)

通过计算 A 的完整奇异值分解来检查结果。将 A 转换成满矩阵并使用 svd。

[U1,S1,V1] = svd(full(A));

使用对数刻度绘制由 svd 和 svds 计算的 A 的六个最大奇异值。

s2 = diag(S1);
semilogy(s2(1:6),'r.')
hold on
semilogy(s,'ro','MarkerSize',10)
title('Singular Values of west0479')
legend('svd','svds')

Figure contains an axes object. The axes object with title Singular Values of west0479 contains 2 objects of type line. One or more of the lines displays its values using only markers These objects represent svd, svds.

解决收敛问题

打开实时脚本

创建一个稀疏对角矩阵并计算六个最大的奇异值。

A = diag(sparse([1e4*ones(1, 8) 1e4:-1:1]));
s = svds(A)

Warning: Only 2 of the 6 requested singular values converged. Singular values that did not converge are NaN.

s = 6×1
10⁴ ×

    1.0000
    0.9999
       NaN
       NaN
       NaN
       NaN

由于已执行完最大迭代次数，但仍然无法满足容差要求，所以 svds 算法生成一条警告消息。

解决收敛问题的最有效方法是使用更大的 'SubspaceDimension' 值，以增加计算中使用的克雷洛夫子空间的最大大小。此操作可通过传入值为 60 的名称-值对组 'SubspaceDimension' 来完成。

s = svds(A,6,'largest','SubspaceDimension',60)

使用 QR 分解计算接近奇异矩阵的 SVD

打开实时脚本

计算接近奇异矩阵的 10 个最小的奇异值。

rng default
format shortg
B = spdiags([repelem([1; 1e-7], [198, 2]) ones(200, 1)], [0 1], 200, 200);
s1 = svds(B,10,'smallest')

Warning: Large residual norm detected. This is likely due to bad condition of the input matrix (condition number 1.0008e+16).

警告表明 svds 无法计算正确的奇异值。svds 失败的原因在于最小奇异值和次小奇异值之间存在间隔。svds(...,'smallest') 需要求 B 的逆矩阵，这会产生较大的数值误差。

要进行比较，请使用 svd 计算精确的奇异值。

s = svd(full(B));
s = s(end-9:end)

要使用 svds 再现此计算，请执行 B 的 QR 分解。三角矩阵 R 的奇异值与 B 的相同。

[Q,R,p] = qr(B,0);

绘制 R 的每行的范数。

rownormR = sqrt(diag(R*R'));
semilogy(rownormR)
hold on;
semilogy(size(R, 1), rownormR(end), 'ro')

Figure contains an axes object. The axes object contains 2 objects of type line. One or more of the lines displays its values using only markers

R 中的最后一项接近于零，这导致解不稳定。

通过将 R 的最后一行精确设置为零，可以防止此项破坏解的正确部分。

R(end,:) = 0;

使用 svds 求出 R 的 10 个最小的奇异值。结果与通过 svd 获得的值类似。

sr = svds(R,10,'smallest')

要使用此方法计算 B 的奇异向量，请使用 Q 和置换向量 p 转换左奇异向量和右奇异向量。

[U,S,V] = svds(R,20,'s');
U = Q*U;
V(p,:) = V;

输入参数

全部折叠

`A` — 输入矩阵
矩阵

输入矩阵。A 通常是（但不总是）一个大型稀疏矩阵。

数据类型: single | double
复数支持: 是

`k` — 要计算的奇异值个数
标量

要计算的奇异值个数，指定为正整数标量。如果满足下列任一条件，svds 返回的奇异值个数将少于请求的数量：

k 大于 min(size(A))
sigma = 'smallestnz' 且 k 大于 A 的非零奇异值个数

如果 k 太大，svds 会将其替换为 k 的最大有效值。

示例: svds(A,2) 返回 A 的两个最大的奇异值。

`sigma` — 奇异值的类型
`'largest'` (默认) | `'smallest'` | `'smallestnz'` | 标量

奇异值的类型，指定为下列值之一。

选项	描述
`'largest'`（默认值）	最大奇异值
`'smallest'`	最小奇异值
`'smallestnz'`	最小非零奇异值
标量	最接近标量的奇异值

示例: svds(A,k,'smallest') 计算 k 个最小奇异值。

示例: svds(A,k,100) 计算与 100 最接近的 k 个奇异值。

数据类型: single | double | char | string

`opts` — Options 结构体
结构体

Options 结构体，指定为包含下表中的一个或多个字段的结构体。

注意

不建议使用 options 结构体指定选项，而应使用名称-值对组。

选项字段	描述	名称-值对组
`tol`	收敛容差	`'Tolerance'`
`maxit`	最大迭代次数	`'MaxIterations'`
`p`	克雷洛夫子空间的最大大小	`'SubspaceDimension'`
`u0`	左初始起始向量	`'LeftStartVector'`
`v0`	右初始起始向量	`'RightStartVector'`
`disp`	诊断信息的显示级别	`'Display'`
`fail`	输出中未收敛的奇异值的处理方式	`'FailureTreatment'`

注意

如果使用数值标量偏移值 sigma，svds 将忽略选项 p。

示例: opts.tol = 1e-6, opts.maxit = 500 将创建一个结构体，其中包含字段 tol 和 maxit 的设置值。

数据类型: struct

`Afun` — 矩阵函数
函数句柄

矩阵函数，指定为函数句柄。函数 Afun 必须满足下列条件：

Afun(x,'notransp') 接受向量 x 并返回乘积 A*x。
Afun(x,'transp') 接受向量 x 并返回乘积 A'*x。

注意

只有在 sigma = 'largest'（默认值）这种情况下，才使用函数句柄。

示例: svds(Afun,[1000 1200])

`n` — `Afun` 使用的矩阵的大小
二元素向量

Afun 使用的 A 矩阵的大小，指定为二元素向量 [m n]。

名称-值参数

全部折叠

以 Name1=Value1,...,NameN=ValueN 的形式指定可选参量对组，其中 Name 是参量名称，Value 是对应的值。名称-值参量必须出现在其他参量之后，但对各个参量对组的顺序没有要求。

在 R2021a 之前，使用逗号分隔每个名称和值，并用引号将 Name 引起来。

示例: s = svds(A,k,sigma,'Tolerance',1e-10,'MaxIterations',100) 放宽收敛容差并使用较少的迭代。

`Tolerance` — 收敛容差
`1e-14` (默认) | 非负实数标量

收敛容差，以逗号分隔的对组形式指定，该对组由 'Tolerance' 和一个非负实数数值标量组成。

示例: s = svds(A,k,sigma,'Tolerance',1e-3)

`MaxIterations` — 算法的最大迭代次数
`300` (默认) | 正整数

算法的最大迭代次数，以逗号分隔的对组形式指定，该对组由 'MaxIterations' 和一个正整数组成。

示例: s = svds(A,k,sigma,'MaxIterations',350)

`SubspaceDimension` — 克雷洛夫子空间的最大大小
`max(3*k,15)` (默认) | 非负整数

克雷洛夫子空间的最大大小，以逗号分隔的对组形式指定，该对组由 'SubspaceDimension' 和一个非负整数组成。'SubspaceDimension' 值必须大于或等于 k + 2，其中 k 是奇异值的数量。

对于 svds 不能收敛的问题，增大 'SubspaceDimension' 的值可以改善收敛行为。

对于数值类型的 sigma，此选项将被忽略。

示例: s = svds(A,k,sigma,'SubspaceDimension',25)

`LeftStartVector` — 左初始起始向量
向量

左初始起始向量，以逗号分隔的对组形式指定，该对组由 'LeftStartVector' 和一个数值向量组成。

您可以指定 'LeftStartVector' 或 'RightStartVector'，但不能同时指定两者。如果未指定任何选项，则对于 m×n 矩阵 A 来说，默认值为：

m < n - 左初始起始向量设置为 randn(m,1)
m >= n - 右初始起始向量设置为 randn(n,1)

指定不同随机起始向量的主要原因是为了控制用于生成向量的随机数流。

注意

svds 使用专用的随机数流以可再现的方式选择起始向量。更改随机数种子不会影响 randn 的这种用法。

示例: s = svds(A,k,sigma,'LeftStartVector',randn(m,1)) 使用从全局随机数流中获取值的随机起始向量。

数据类型: single | double

`RightStartVector` — 右初始起始向量
向量

右初始起始向量，以逗号分隔的对组形式指定，该对组由 'RightStartVector' 和一个数值向量组成。

您可以指定 'LeftStartVector' 或 'RightStartVector'，但不能同时指定两者。如果未指定任何选项，则对于 m×n 矩阵 A 来说，默认值为：

m < n - 左初始起始向量设置为 randn(m,1)
m >= n - 右初始起始向量设置为 randn(n,1)

指定不同随机起始向量的主要原因是为了控制用于生成向量的随机数流。

注意

svds 使用专用的随机数流以可再现的方式选择起始向量。更改随机数种子不会影响 randn 的这种用法。

示例: s = svds(A,k,sigma,'RightStartVector',randn(n,1)) 使用从全局随机数流中获取值的随机起始向量。

数据类型: single | double

`FailureTreatment` — 未收敛的奇异值的处理方式
`'replacenan'` | `'keep'` | `'drop'`

未收敛的奇异值的处理方式，以逗号分隔的对组形式指定，该对组由 'FailureTreatment' 和下列选项之一组成：'replacenan'、'keep' 或 'drop'。

'FailureTreatment' 的值决定未收敛的奇异值在输出中如何显示。

选项	对输出的影响
`'drop'`	从输出中删除未收敛的奇异值，这会导致 `svds` 返回的奇异值数量少于请求的数量。对于数值类型的 `sigma`，此值为默认值。
`'replacenan'`	将未收敛的奇异值替换为 `NaN` 值。对于非数值类型的 `sigma`，此值为默认值。
`'keep'`	在输出中包括未收敛的奇异值。

示例: s = svds(A,k,sigma,'FailureTreatment','drop') 将从输出中删除未收敛的奇异值。

数据类型: char | string

`Display` — 开启或关闭诊断信息的显示
`false` (默认) | `true` | `0` | `1`

开启或关闭诊断信息的显示，指定为 false、true、0 或 1。值 false 或 0 将关闭显示，值 true 或 1 将开启显示。

输出参量

全部折叠

`s` — 奇异值
列向量

奇异值，以列向量形式返回。奇异值是以降序顺序列出的非负实数。

`U` — 左奇异向量
矩阵

左奇异向量，以矩阵的列形式返回。如果 A 是一个 m×n 矩阵，而您请求 k 个奇异值，则 U 将是一个包含正交列的 m×k 矩阵。

不同的计算机、MATLAB^® 版本或参数（例如起始向量和子空间维度）可能生成不同的奇异向量，它们在数值上依然精确。U 和 V 中的相应列可以翻转其符号，因为这不会影响表达式 A = U*S*V' 的值。

`S` — 奇异值
对角矩阵

奇异值，以对角矩阵形式返回。S 的对角元素是非负奇异值。如果 A 是一个 m×n 矩阵，而您请求 k 个奇异值，则 S 将是一个 k×k 矩阵。

`V` — 右奇异向量
矩阵

右奇异向量，以矩阵的列形式返回。如果 A 是一个 m×n 矩阵，而您请求 k 个奇异值，则 V 将是一个包含正交列的 n×k 矩阵。

不同的计算机、MATLAB 版本或参数（例如起始向量和子空间维度）可能生成不同的奇异向量，它们在数值上依然精确。U 和 V 中的相应列可以翻转其符号，因为这不会影响表达式 A = U*S*V' 的值。

`flag` — 收敛标志
标量

收敛标志，以标量形式返回。值为 0 表示所有奇异值已收敛。否则，表示并非所有奇异值均已收敛。

使用此收敛标志输出可抑制收敛失败时的警告。

提示

如果您事先不知道用 svds 指定什么秩但知道 SVD 的逼近应满足什么容差，则 svdsketch 很有用。
svds 使用专用的随机数流生成默认起始向量，以确保在不同运行之间的可再现性。调用 svds 之前使用 rng 设置随机数生成器状态不会影响输出。
要求出小型稠密矩阵的几个奇异值，使用 svds 并不是最有效的方式。对于这些问题，使用 svd(full(A)) 可能会更快。例如，求 500×500 矩阵中的三个奇异值相对容易，使用 svd 即可轻松完成。
对于给定矩阵，如果 svds 无法收敛，可以通过增大 'SubspaceDimension' 值来增加克雷洛夫子空间的大小。作为备用方案，调整最大迭代次数 ('MaxIterations') 和收敛容差 ('Tolerance') 也有助于改善收敛行为。
增大 k 有时可以提高性能，特别是当矩阵包含重复的奇异值时。

参考

[1] Baglama, J. and L. Reichel, “Augmented Implicitly Restarted Lanczos Bidiagonalization Methods.” SIAM Journal on Scientific Computing. Vol. 27, 2005, pp. 19–42.

[2] Larsen, R. M. “Lanczos Bidiagonalization with partial reorthogonalization.” Dept. of Computer Science, Aarhus University. DAIMI PB-357, 1998.

扩展功能

全部展开

基于线程的环境
使用 MATLAB® `backgroundPool` 在后台运行代码或使用 Parallel Computing Toolbox™ `ThreadPool` 加快代码运行速度。

此函数完全支持基于线程的环境。有关详细信息，请参阅在基于线程的环境中运行 MATLAB 函数。

GPU 数组
通过使用 Parallel Computing Toolbox™ 在图形处理单元 (GPU) 上运行来加快代码执行。

svds 函数支持 GPU 数组输入，但有以下用法说明和限制：

如果提供 sigma 参数，则值必须为 'largest'。
输入矩阵 A 必须为 double 类型。

有关详细信息，请参阅在 GPU 上运行 MATLAB 函数 (Parallel Computing Toolbox)。

分布式数组
使用 Parallel Computing Toolbox™ 在集群的组合内存中对大型数组进行分区。

用法说明和限制：

如果提供 sigma 参数，则值必须为 'largest'。
输入矩阵 A 必须为 double 类型。

有关详细信息，请参阅使用分布式数组运行 MATLAB 函数 (Parallel Computing Toolbox)。

版本历史记录

在 R2006a 之前推出

全部展开

R2025a: 指定单精度输入参量

您可以将以下参量指定为单精度：

A - 输入矩阵
sigma - 特征值的类型
LeftStartVector - 左初始起始向量
RightStartVector - 右初始起始向量

如果将 A、LeftStartVector 或 RightStartVector 指定为单精度，函数将以单精度计算并返回 single 类型的输出。

如果仅指定矩阵函数 Afun 和矩阵大小 n 作为输入，svds 的输出的精度与 Afun 的输出相同。如果还将 LeftStartVector 或 RightStartVector 指定为 single，则 Afun 的输出也必须为 single。

R2016a: 可再现性变化

可再现性
现在，连续多次调用 svds 会产生相同的结果。要更改此行为，请执行以下操作：
- 在 R2017a 或更早版本中，将 options 结构体的 u0 或 v0 字段设置为随机向量。
- 在 R2017b 或更高版本中，优先选择将 'LeftStartVector' 或 'RightStartVector' 设置为随机向量。

另请参阅

svd | eigs | svdsketch | svdappend

主题

奇异值

svds

语法

说明

示例

最大奇异值

最小奇异值

最小非零奇异值

使用函数句柄的最大奇异值

稀疏矩阵的奇异值分解

解决收敛问题

使用 QR 分解计算接近奇异矩阵的 SVD

输入参数

A — 输入矩阵 矩阵

k — 要计算的奇异值个数 标量

sigma — 奇异值的类型 'largest' (默认) | 'smallest' | 'smallestnz' | 标量

opts — Options 结构体 结构体

Afun — 矩阵函数 函数句柄

n — Afun 使用的矩阵的大小 二元素向量

名称-值参数

Tolerance — 收敛容差 1e-14 (默认) | 非负实数标量

MaxIterations — 算法的最大迭代次数 300 (默认) | 正整数

SubspaceDimension — 克雷洛夫子空间的最大大小 max(3*k,15) (默认) | 非负整数

LeftStartVector — 左初始起始向量 向量

RightStartVector — 右初始起始向量 向量

FailureTreatment — 未收敛的奇异值的处理方式 'replacenan' | 'keep' | 'drop'

Display — 开启或关闭诊断信息的显示 false (默认) | true | 0 | 1

输出参量

s — 奇异值 列向量

U — 左奇异向量 矩阵

S — 奇异值 对角矩阵

V — 右奇异向量 矩阵

flag — 收敛标志 标量

提示

参考

扩展功能

基于线程的环境 使用 MATLAB® backgroundPool 在后台运行代码或使用 Parallel Computing Toolbox™ ThreadPool 加快代码运行速度。

GPU 数组 通过使用 Parallel Computing Toolbox™ 在图形处理单元 (GPU) 上运行来加快代码执行。

分布式数组 使用 Parallel Computing Toolbox™ 在集群的组合内存中对大型数组进行分区。

版本历史记录

R2025a: 指定单精度输入参量

R2016a: 可再现性变化

另请参阅

主题

`A` — 输入矩阵
矩阵

`k` — 要计算的奇异值个数
标量

`sigma` — 奇异值的类型
`'largest'` (默认) | `'smallest'` | `'smallestnz'` | 标量

`opts` — Options 结构体
结构体

`Afun` — 矩阵函数
函数句柄

`n` — `Afun` 使用的矩阵的大小
二元素向量

`Tolerance` — 收敛容差
`1e-14` (默认) | 非负实数标量

`MaxIterations` — 算法的最大迭代次数
`300` (默认) | 正整数

`SubspaceDimension` — 克雷洛夫子空间的最大大小
`max(3*k,15)` (默认) | 非负整数

`LeftStartVector` — 左初始起始向量
向量

`RightStartVector` — 右初始起始向量
向量

`FailureTreatment` — 未收敛的奇异值的处理方式
`'replacenan'` | `'keep'` | `'drop'`

`Display` — 开启或关闭诊断信息的显示
`false` (默认) | `true` | `0` | `1`

`s` — 奇异值
列向量

`U` — 左奇异向量
矩阵

`S` — 奇异值
对角矩阵

`V` — 右奇异向量
矩阵

`flag` — 收敛标志
标量

基于线程的环境
使用 MATLAB® `backgroundPool` 在后台运行代码或使用 Parallel Computing Toolbox™ `ThreadPool` 加快代码运行速度。

GPU 数组
通过使用 Parallel Computing Toolbox™ 在图形处理单元 (GPU) 上运行来加快代码执行。

分布式数组
使用 Parallel Computing Toolbox™ 在集群的组合内存中对大型数组进行分区。