计算量化误差
此示例说明如何计算和比较使用各种舍入方法时信号量化误差的统计量。当某数据类型无法精确表示某个值时,就会发生量化。在这些情况下,必须将该值舍入到该数据类型可以表示的最接近的值。
首先,创建一个跨 quantizer 对象范围的随机信号。接下来,分别使用舍入方法 'fix'、'floor'、'ceil'、'nearest' 和 'convergent' 对信号进行量化,并估计信号的统计量。
使用 errpdf 函数计算量化误差的理论概率密度函数,使用 errmean 函数计算量化误差的理论均值,使用 errvar 函数计算量化误差的理论方差。
创建均匀分布的随机信号
创建一个均匀分布的随机信号,其范围跨定点 quantizer 对象 q 的 -1 到 1 域。
q = quantizer([8 7]); r = realmax(q); u = r*(2*rand(50000,1) - 1); xi = linspace(-2*eps(q),2*eps(q),256);
fix:向零舍入
使用 'fix' 舍入时,概率密度函数的宽度是其他方法的两倍。因此,方差是其他方法的四倍。
q = quantizer('fix',[8 7]);
err = quantize(q,u) - u;
f_t = errpdf(q,xi);
mu_t = errmean(q);
v_t = errvar(q);
qerrordemoplot(q,f_t,xi,mu_t,v_t,err)Estimated error variance (dB) = -46.8586 Theoretical error variance (dB) = -46.9154 Estimated mean = 7.788e-06 Theoretical mean = 0
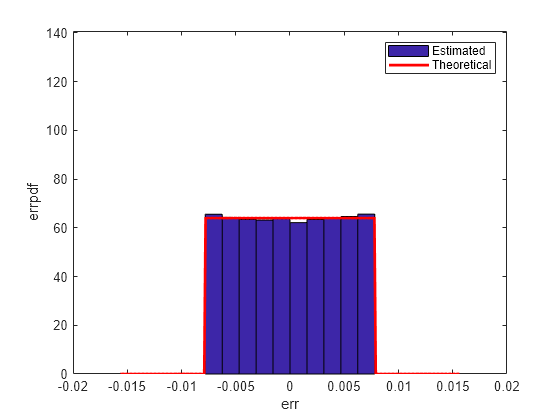
理论方差为 eps(q)^2/3,理论均值为 0。
floor:向负无穷方向舍入
当与使用 2 的补码表示的整数和定点数结合使用时,'floor' 舍入通常称为截断。它是 DSP 处理器最常见的舍入模式,因为它不需要硬件来实现。'floor' 不会产生像 'round' 那样接近真实值的量化值,但它具有相同的方差。使用 'floor' 时,会检测到符号变化的小信号,而在 'round' 中它们会丢失。
q = quantizer('floor',[8 7]);
err = quantize(q,u) - u;
f_t = errpdf(q,xi);
mu_t = errmean(q);
v_t = errvar(q);
qerrordemoplot(q,f_t,xi,mu_t,v_t,err)Estimated error variance (dB) = -52.9148 Theoretical error variance (dB) = -52.936 Estimated mean = -0.0038956 Theoretical mean = -0.0039062
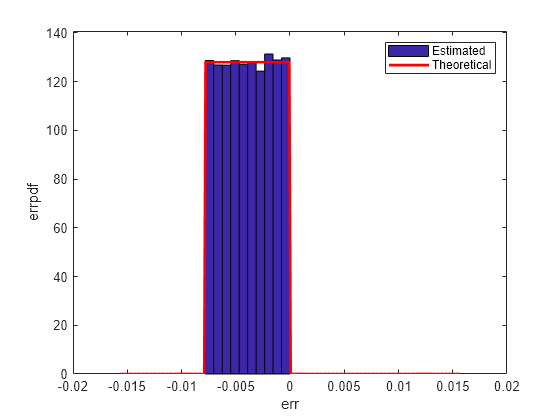
理论方差为 eps(q)^2/12,理论均值为 -eps(q)/2。
Ceil:向正无穷方向舍入
q = quantizer('ceil',[8 7]);
err = quantize(q,u) - u;
f_t = errpdf(q,xi);
mu_t = errmean(q);
v_t = errvar(q);
qerrordemoplot(q,f_t,xi,mu_t,v_t,err)Estimated error variance (dB) = -52.9148 Theoretical error variance (dB) = -52.936 Estimated mean = 0.0039169 Theoretical mean = 0.0039062
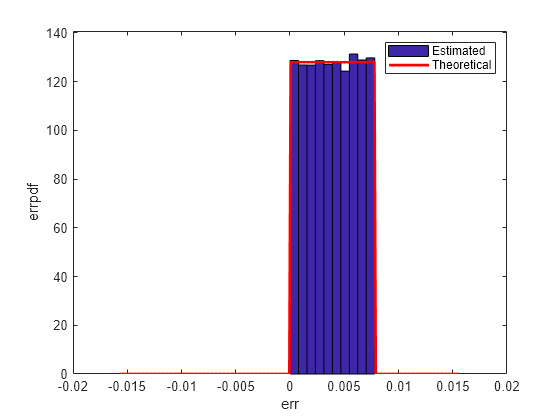
理论方差为 eps(q)^2/12,理论均值为 eps(q)/2。
round:舍入到最接近的值;出现结值时舍入到最大幅值
'round' 比 'floor' 更准确,但所有小于 eps(q) 的值都会舍入为零并丢失。
q = quantizer('nearest',[8 7]);
err = quantize(q,u) - u;
f_t = errpdf(q,xi);
mu_t = errmean(q);
v_t = errvar(q);
qerrordemoplot(q,f_t,xi,mu_t,v_t,err)Estimated error variance (dB) = -52.9579 Theoretical error variance (dB) = -52.936 Estimated mean = -2.212e-06 Theoretical mean = 0
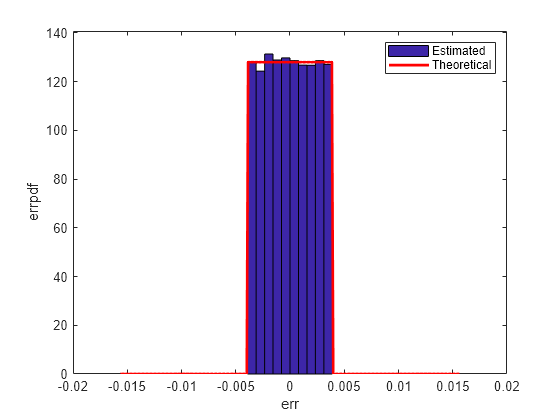
理论方差为 eps(q)^2/12,理论均值为 0。
convergent:舍入到最接近的值;出现结值时舍入到偶数
'convergent' 舍入消除了由普通 'round' 引入的偏差,该偏差是由于始终以相同方向舍入结值引起的。
q = quantizer('convergent',[8 7]);
err = quantize(q,u) - u;
f_t = errpdf(q,xi);
mu_t = errmean(q);
v_t = errvar(q);
qerrordemoplot(q,f_t,xi,mu_t,v_t,err)Estimated error variance (dB) = -52.9579 Theoretical error variance (dB) = -52.936 Estimated mean = -2.212e-06 Theoretical mean = 0

理论方差为 eps(q)^2/12,理论均值为 0。
比较最近舍入和收敛舍入
通过查看绘图,很难区分收敛舍入的误差概率密度函数和最近舍入的误差概率密度函数。
收敛的误差概率密度函数为
f(err) = 1/eps(q), for -eps(q)/2 <= err <= eps(q)/2, and 0 otherwise
而舍入的误差概率密度函数为
f(err) = 1/eps(q), for -eps(q)/2 < err <= eps(q)/2, and 0 otherwise
收敛的误差概率密度函数是对称的,而舍入则略微偏向正值。
唯一区别是出现结值时的舍入方向。
x = (-3.5:3.5)'; [x convergent(x) nearest(x)]
ans = 8×3
-3.5000 -4.0000 -3.0000
-2.5000 -2.0000 -2.0000
-1.5000 -2.0000 -1.0000
-0.5000 0 0
0.5000 0 1.0000
1.5000 2.0000 2.0000
2.5000 2.0000 3.0000
3.5000 4.0000 4.0000