Extended Object Tracking of Highway Vehicles with Radar and Camera

Introduction

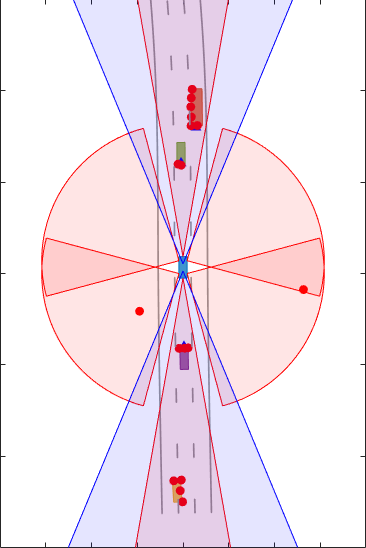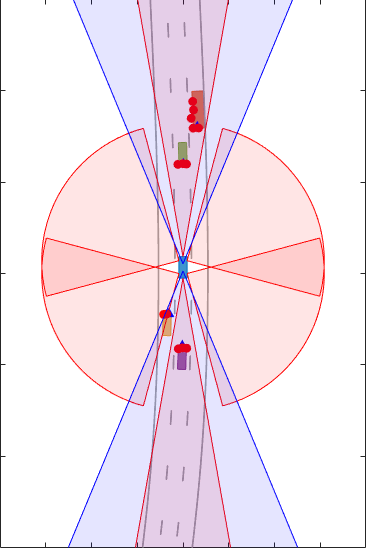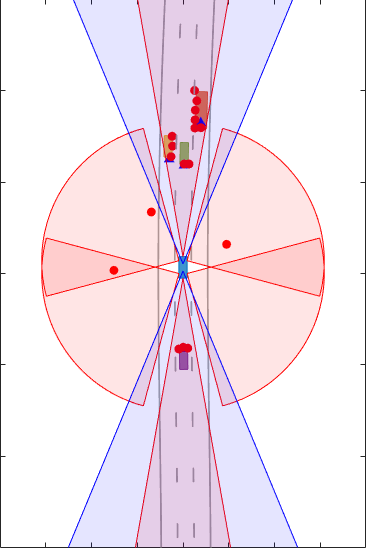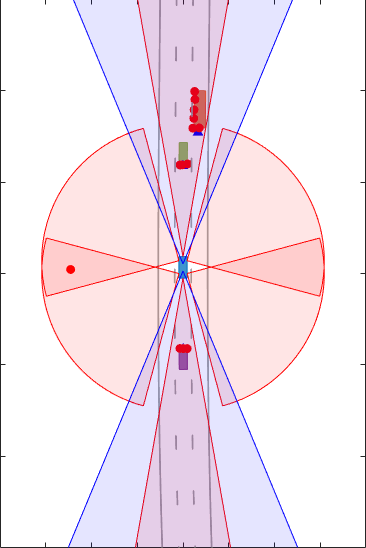
In conventional tracking approaches such as global nearest neighbor (multiObjectTracker, trackerGNN), joint probabilistic data association (trackerJPDA) and multi-hypothesis tracking (trackerTOMHT), tracked objects are assumed to return one detection per sensor scan. With the development of sensors that have better resolution, such as a high-resolution radar, the sensors typically return more than one detection of an object. For example, the image below depicts multiple detections for a single vehicle that spans multiple radar resolution cells. In such cases, the technique used to track the objects is known as extended object tracking [1].

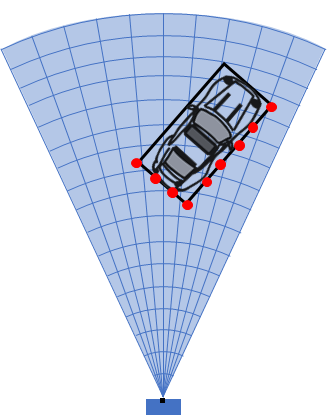
The key benefit of using a high-resolution sensor is getting more information about the object, such as its dimensions and orientation. This additional information can improve the probability of detection and reduce the false alarm rate.

Extended objects present new challenges to conventional trackers, because these trackers assume a single detection per object per sensor. In some cases, you can cluster the sensor data to provide the conventional trackers with a single detection per object. However, by doing so, the benefit of using a high-resolution sensor may be lost.

In contrast, extended object trackers can handle multiple detections per object. In addition, these trackers can estimate not only the kinematic states, such as position and velocity of the object, but also the dimensions and orientation of the object. In this example, you track vehicles around the ego vehicle using the following trackers:

You will evaluate the tracking results of all trackers using trackErrorMetrics and trackAssignmentMetrics, which provide multiple measures of effectiveness of a tracker. You will also evaluate the results using the Optimal SubPattern Assignment Metric (OSPA), trackOSPAMetric, which aims to evaluate the performance of a tracker using a combined score.

Setup

Scenario

In this example, there is an ego vehicle and four other vehicles: a vehicle ahead of the ego vehicle in the center lane, a vehicle behind the ego vehicle in the center lane, a truck ahead of the ego vehicle in the right lane and an overtaking vehicle in the left lane.

In this example, you simulate an ego vehicle that has 6 radar sensors and 2 vision sensors covering the 360-degree field of view. The sensors have some overlap and some coverage gap. The ego vehicle is equipped with a long-range radar sensor and a vision sensor on both the front and back of the vehicle. Each side of the vehicle has two short-range radar sensors, each covering 90 degrees. One sensor on each side covers from the middle of the vehicle to the back. The other sensor on each side covers from the middle of the vehicle forward.

% Create the scenario
[scenario, egoVehicle, sensors] = helperCreateScenario;

% Create the display object
display = helperExtendedTargetTrackingDisplay;

% Create the Animation writer to record each frame of the figure for
% animation writing. Set 'RecordGIF' to true to enable GIF writing.
gifWriter = helperGIFWriter(Figure = display.Figure,...
    RecordGIF = false);

Metrics

In this example, you use some key metrics to assess the tracking performance of each tracker. In particular, you assess the trackers based on their accuracy in estimating the positions, velocities, dimensions (length and width) and orientations of the objects. These metrics can be evaluated using the trackErrorMetrics class. To define the error of a tracked target from its ground truth, this example uses a 'custom' error function, helperExtendedTargetError, listed at the end of this example.

You will also assess the performance based on metrics such as number of false tracks or redundant tracks. These metrics can be calculated using the trackAssignmentMetrics class. To define the distance between a tracked target and a truth object, this example uses a 'custom' error function, helperExtendedTargetDistance, listed at the end of this example. The function defines the distance metric as the sum of distances in position, velocity, dimension and yaw.

trackErrorMetrics and trackAssignmentMetrics provide multiple measures of effectiveness of a tracking algorithm. You will also assess the performance based on the Optimal SubPattern Assignment Metric (OSPA), which provides a single score value for the tracking algorithm at each time step. This metric can be calculated using the trackOSPAMetric class. The 'custom' distance function defined for OSPA is same as the assignment metrics.

% Function to return the errors given track and truth.
errorFcn = @(track,truth)helperExtendedTargetError(track,truth);

% Function to return the distance between track and truth.
distFcn = @(track,truth)helperExtendedTargetDistance(track,truth);

% Function to return the IDs from the ground truth. The default
% identifier assumes that the truth is identified with PlatformID. In
% drivingScenario, truth is identified with an ActorID.
truthIdFcn = @(x)[x.ActorID];

% Create metrics object.
tem = trackErrorMetrics(...
    ErrorFunctionFormat = 'custom',...
    EstimationErrorLabels = {'PositionError','VelocityError','DimensionsError','YawError'},...
    EstimationErrorFcn = errorFcn,...
    TruthIdentifierFcn = truthIdFcn);

tam = trackAssignmentMetrics(...
    DistanceFunctionFormat = 'custom',...
    AssignmentDistanceFcn = distFcn,...
    DivergenceDistanceFcn = distFcn,...
    TruthIdentifierFcn = truthIdFcn,...
    AssignmentThreshold = 30,...
    DivergenceThreshold = 35);

% Create ospa metric object.
tom = trackOSPAMetric(...
    Distance = 'custom',...
    DistanceFcn = distFcn,...
    TruthIdentifierFcn = truthIdFcn);

Point Object Tracker

The multiObjectTracker System object™ assumes one detection per object per sensor and uses a global nearest neighbor approach to associate detections to tracks. It assumes that every object can be detected at most once by a sensor in a scan. In this case, the simulated radar sensors have a high enough resolution to generate multiple detections per object. If these detections are not clustered, the tracker generates multiple tracks per object. Clustering returns one detection per cluster, at the cost of having a larger uncertainty covariance and losing information about the true object dimensions. Clustering also makes it hard to distinguish between two objects when they are close to each other, for example, when one vehicle passes another vehicle.

trackerRunTimes = zeros(0,3);
ospaMetric = zeros(0,3);

% Create a multiObjectTracker
tracker = multiObjectTracker(...
    FilterInitializationFcn = @helperInitPointFilter, ...
    AssignmentThreshold = 30, ...
    ConfirmationThreshold = [4 5], ...
    DeletionThreshold = 3);

% Reset the random number generator for repeatable results
seed = 2018;
S = rng(seed);
timeStep = 1;

% For multiObjectTracker, the radar reports in Ego Cartesian frame and does
% not report velocity. This allows us to cluster detections from multiple
% sensors.
for i = 1:6
    sensors{i}.HasRangeRate = false;
    sensors{i}.DetectionCoordinates = 'Body';
end

Run the scenario.

while advance(scenario) && ishghandle(display.Figure)
    % Get the scenario time
    time = scenario.SimulationTime;

    % Collect detections from the ego vehicle sensors
    [detections,isValidTime] = helperDetect(sensors, egoVehicle, time);

    % Update the tracker if there are new detections
    if any(isValidTime)
        % Detections must be clustered first for the point tracker
        detectionClusters = helperClusterRadarDetections(detections);

        % Update the tracker
        tic
        % confirmedTracks are in scenario coordinates
        confirmedTracks = updateTracks(tracker, detectionClusters, time);
        t = toc;

        % Update the metrics
        % a. Obtain ground truth
        groundTruth = scenario.Actors(2:end); % All except Ego

        % b. Update assignment metrics
        tam(confirmedTracks,groundTruth);
        [trackIDs,truthIDs] = currentAssignment(tam);

        % c. Update error metrics
        tem(confirmedTracks,trackIDs,groundTruth,truthIDs);

        % d. Update ospa metric
        ospaMetric(timeStep,1) = tom(confirmedTracks, groundTruth);

        % Update bird's-eye-plot
        % Convert tracks to ego coordinates for display
        confirmedTracksEgo = helperConvertToEgoCoordinates(egoVehicle, confirmedTracks);
        display(egoVehicle, sensors, detections, confirmedTracksEgo, detectionClusters);
        drawnow;

        % Record tracker run times
        trackerRunTimes(timeStep,1) = t;
        timeStep = timeStep + 1;

        % Capture frames for animation
        gifWriter();
    end
end

% Capture the cumulative track metrics. The error metrics show the averaged
% value of the error over the simulation.
assignmentMetricsMOT = tam.trackMetricsTable;
errorMetricsMOT = tem.cumulativeTruthMetrics;

% Write GIF if requested
writeAnimation(gifWriter,'multiObjectTracking');

These results show that, with clustering, the tracker can keep track of the objects in the scene. However, it also shows that the track associated with the overtaking vehicle (yellow) moves from the front of the vehicle at the beginning of the scenario to the back of the vehicle at the end. At the beginning of the scenario, the overtaking vehicle is behind the ego vehicle (blue), so radar and vision detections are made from its front. As the overtaking vehicle passes the ego vehicle, radar detections are made from the side of the overtaking vehicle and then from its back, and the track moves to the back of the vehicle.

You can also see that the clustering is not perfect. When the passing vehicle passes the vehicle that is behind the ego vehicle (purple), both tracks are slightly shifted to the left due to the imperfect clustering. A redundant track is created on the track initially due to multiple clusters created when part of the side edge is missed. Also, a redundant track appears on the passing vehicle during the end because the distances between its detections increase.

GGIW-PHD Extended Object Tracker

In this section, you use a GGIW-PHD tracker (trackerPHD with ggiwphd) to track objects. Unlike multiObjectTracker, which uses one filter per track, the GGIW-PHD is a multi-target filter which describes the probability hypothesis density (PHD) of the scenario. To model the extended target, GGIW-PHD uses the following distributions:

Gamma: Positive value to describe expected number of detections.

Gaussian: State vector to describe target's kinematic state.

Inverse-Wishart: Positive-definite matrix to describe the elliptical extent.

The model assumes that each distribution is independent of each other. Thus, the probability hypothesis density (PHD) in GGIW-PHD filter is described by a weighted sum of the probability density functions of several GGIW components.

A PHD tracker requires calculating the detectability of each component in the density. The calculation of detectability requires configurations of each sensor used with the tracker. You define these configurations for trackerPHD using the trackingSensorConfiguration class.

% Release and restart all objects.
restart(scenario);
release(tem);
release(tam);
% No penality for trackerPHD
tam.AssignmentThreshold = tam.AssignmentThreshold - 2;
release(display);
display.PlotClusteredDetection = false;
gifWriter.pFrames = {};
for i = 1:numel(sensors)
    release(sensors{i});
    if i <= 6
        sensors{i}.HasRangeRate = true;
        sensors{i}.DetectionCoordinates = 'Sensor spherical';
    end
end

% Restore random seed.
rng(seed)

% Set up sensor configurations

% Set Ego pose
egoPose.Position = egoVehicle.Position;
egoPose.Velocity = egoVehicle.Velocity;
egoPose.Orientation = rotmat(quaternion([egoVehicle.Yaw egoVehicle.Pitch egoVehicle.Roll],'eulerd','ZYX','frame'),'frame');

sensorConfigurations = cell(numel(sensors),1);
for i = 1:numel(sensors)
    sensorConfigurations{i}  = trackingSensorConfiguration(sensors{i},egoPose, ...
        FilterInitializationFcn = @helperInitGGIWFilter, ...
        SensorTransformFcn = @ctmeas);
end

Define the tracker.

In contrast to a point object tracker, which usually takes into account one partition (cluster) of detections, the trackerPHD creates multiple possible partitions of a set of detections and evaluates it against the current components in the PHD filter. The 3 and 5 in the function below defines the lower and upper Mahalanobis distance between detections. This is equivalent to defining that each cluster of detection must be a minimum of 3 resolutions apart and maximum of 5 resolutions apart from each other. The helper function wraps around partitionDetections and doesn't use range-rate measurements for partitioning detections from side radars.

partFcn = @(x)helperPartitioningFcn(x,3,5);

tracker = trackerPHD( SensorConfigurations = sensorConfigurations,...
    PartitioningFcn = partFcn,...
    AssignmentThreshold = 450,...% Minimum negative log-likelihood of a detection cell (multiple detections per cell) to add birth components.
    ExtractionThreshold = 0.75,...% Weight threshold of a filter component to be declared a track
    ConfirmationThreshold = 0.85,...% Weight threshold of a filter component to be declared a confirmed track
    MergingThreshold = 50,...% Threshold to merge components
    HasSensorConfigurationsInput = true... % Tracking is performed in scenario frame and hence sensor configurations change with time
    );

Run the simulation. First time step

timeStep = 1;
% Run the scenario
while advance(scenario) && ishghandle(display.Figure)
    % Get the scenario time
    time = scenario.SimulationTime;

    % Get the poses of the other vehicles in ego vehicle coordinates
    ta = targetPoses(egoVehicle);

    % Collect detections from the ego vehicle sensors
    [detections, isValidTime, configurations] = helperDetect(sensors, egoVehicle, time);

    % Update the tracker with all the detections. Note that there is no
    % need to cluster the detections before passing them to the tracker.
    % Also, the sensor configurations are passed as an input to the
    % tracker.
    tic
    % confirmedTracks are in scenario coordinates
    confirmedTracks = tracker(detections,configurations,time);
    t = toc;

    % Update the metrics
    % a. Obtain ground truth
    groundTruth = scenario.Actors(2:end); % All except Ego

    % b. Update assignment metrics
    tam(confirmedTracks,groundTruth);
    [trackIDs,truthIDs] = currentAssignment(tam);

    % c. Update error metrics
    tem(confirmedTracks,trackIDs,groundTruth,truthIDs);

    % d. Update ospa metric
    ospaMetric(timeStep,2) = tom(confirmedTracks, groundTruth);

    % Update the bird's-eye plot
    % Convert tracks to ego coordinates for display
    confirmedTracksEgo = helperConvertToEgoCoordinates(egoVehicle, confirmedTracks);
    display(egoVehicle, sensors, detections, confirmedTracksEgo);
    drawnow;

    % Record tracker run times
    trackerRunTimes(timeStep,2) = t;
    timeStep = timeStep + 1;

    % Capture frames for GIF
    gifWriter();
end

% Capture the truth and track metrics tables
assignmentMetricsGGIWPHD = tam.trackMetricsTable;
errorMetricsGGIWPHD = tem.cumulativeTruthMetrics;

% Write GIF if requested
writeAnimation(gifWriter,'ggiwphdTracking');

These results show that the GGIW-PHD can handle multiple detections per object per sensor, without the need to cluster these detections first. Moreover, by using the multiple detections, the tracker estimates the position, velocity, dimensions and orientation of each object. The dashed elliptical shape in the figure demonstrates the expected extent of the target. The filter initialization function specifies multiple possible sizes and their relative weights using multiple components. The list can be expanded to add more sizes with added computational complexity. In contrast, you can also initialize one component per detection with a higher uncertainty in dimensions. This will enable the tracker to estimate the dimensions of the objects automatically. That said, the accuracy of the estimate will depend on the observability of the target dimensions and is susceptible to shrinkage and enlargement of track dimensions as the targets move around the ego vehicle.

The GGIW-PHD filter assumes that detections are distributed around the target's elliptical center. Therefore, the tracks tend to follow observable portions of the vehicle. Such observable portions include rear face of the vehicle that is directly ahead of the ego vehicle or the front face of the vehicle directly behind the ego vehicle for example, the rear and front face of the vehicle directly ahead and behind of the ego vehicle respectively. In contrast, the length and width of the passing vehicle was fully observed during the simulation. Therefore, its estimated ellipse has a better overlap with the actual shape.

GM-PHD Rectangular Object Tracker

In this section, you use a GM-PHD tracker (trackerPHD with gmphd) and a rectangular target model (initctrectgmphd) to track objects. Unlike ggiwphd, which uses an elliptical shape to track extent, gmphd allows you to use a Gaussian distribution to define the shape of your choice. The rectangular target model is defined by motion models, ctrect and ctrectjac and measurement models, ctrectmeas and ctrectmeasjac.

The sensor configurations defined for trackerPHD earlier remain the same, except for definition of SensorTransformFcn and FilterInitializationFcn.

for i = 1:numel(sensorConfigurations)
    sensorConfigurations{i}.FilterInitializationFcn = @helperInitRectangularFilter; % Initialize a rectangular target gmphd
    sensorConfigurations{i}.SensorTransformFcn = @ctrectcorners; % Use corners to calculate detection probability
end

% Define tracker using new sensor configurations
tracker = trackerPHD( SensorConfigurations = sensorConfigurations,...
    PartitioningFcn = partFcn,...
    AssignmentThreshold = 750,...% Minimum negative log-likelihood of a detection cell to add birth components
    ExtractionThreshold = 0.85,...% Weight threshold of a filter component to be declared a track
    ConfirmationThreshold = 0.95,...% Weight threshold of a filter component to be declared a confirmed track
    MergingThreshold = 50,...% Threshold to merge components
    HasSensorConfigurationsInput = true... % Tracking is performed in scenario frame and hence sensor configurations change with time
    );

% Release and restart all objects.
restart(scenario);
for i = 1:numel(sensors)
    release(sensors{i});
end
release(tem);
release(tam);
release(display);
display.PlotClusteredDetection = false;
gifWriter.pFrames = {};

% Restore random seed.
rng(seed)

% First time step
timeStep = 1;

% Run the scenario
while advance(scenario) && ishghandle(display.Figure)
    % Get the scenario time
    time = scenario.SimulationTime;

    % Get the poses of the other vehicles in ego vehicle coordinates
    ta = targetPoses(egoVehicle);

    % Collect detections from the ego vehicle sensors
    [detections, isValidTime, configurations] = helperDetect(sensors, egoVehicle, time);

    % Update the tracker with all the detections. Note that there is no
    % need to cluster the detections before passing them to the tracker.
    % Also, the sensor configurations are passed as an input to the
    % tracker.
    tic
    % confirmedTracks are in scenario coordinates
    confirmedTracks = tracker(detections,configurations,time);
    t = toc;

    % Update the metrics
    % a. Obtain ground truth
    groundTruth = scenario.Actors(2:end); % All except Ego

    % b. Update assignment metrics
    tam(confirmedTracks,groundTruth);
    [trackIDs,truthIDs] = currentAssignment(tam);

    % c. Update error metrics
    tem(confirmedTracks,trackIDs,groundTruth,truthIDs);

    % d. Update ospa metric
    ospaMetric(timeStep,3) = tom(confirmedTracks, groundTruth);

    % Update the bird's-eye plot
    % Convert tracks to ego coordinates for display
    confirmedTracksEgo = helperConvertToEgoCoordinates(egoVehicle, confirmedTracks);
    display(egoVehicle, sensors, detections, confirmedTracksEgo);
    drawnow;

    % Record tracker run times
    trackerRunTimes(timeStep,3) = t;
    timeStep = timeStep + 1;

    % Capture frames for GIF
    gifWriter();
end

% Capture the truth and track metrics tables
assignmentMetricsGMPHD = tam.trackMetricsTable;
errorMetricsGMPHD = tem.cumulativeTruthMetrics;

% Write GIF if requested
writeAnimation(gifWriter,'gmphdTracking');

% Return the random number generator to its previous state
rng(S)

These results show that the GM-PHD can also handle multiple detections per object per sensor. Similar to GGIW-PHD, it also estimates the size and orientation of the object. The filter initialization function uses a similar approach as the GGIW-PHD tracker and initializes multiple components for different sizes.

You can notice that the estimated tracks, which are modeled as rectangles, have a good fit with the simulated ground truth object, depicted by the solid color patches. In particular, the tracks are able to correctly track the shape of the vehicle along with the kinematic center.

Evaluate Tracking Performance

Evaluate the tracking performance of each tracker using quantitative metrics such as the estimation error in position, velocity, dimensions and orientation. Also evaluate the track assignments using metrics such as redundant and false tracks.

Assignment metrics

helperPlotAssignmentMetrics(assignmentMetricsMOT, assignmentMetricsGGIWPHD, assignmentMetricsGMPHD);

The assignment metrics illustrate that redundant and false tracks were initialized and confirmed by the point object tracker. These tracks result due to imperfect clustering, where detections belonging to the same target were clustered into more than one clustered detection. In contrast, the GGIW-PHD tracker and the GM-PHD tracker maintain tracks on all four targets and do not create any false or redundant tracks. These metrics show that both extended object trackers correctly partition the detections and associate them with the correct tracks.

Error metrics

helperPlotErrorMetrics(errorMetricsMOT, errorMetricsGGIWPHD, errorMetricsGMPHD);

The plot shows the average estimation errors for the three types of trackers used in this example. Because the point object tracker does not estimate the yaw and dimensions of the objects, they are now shown in the plots. The point object tracker is able to estimate the kinematics of the objects with a reasonable accuracy. The position error of the vehicle behind the ego vehicle is higher because it was dragged to the left when the passing vehicle overtakes this vehicle. This is also an artifact of imperfect clustering when the objects are close to each other.

As described earlier, the GGIW-PHD tracker assumes that measurements are distributed around the object's extent, which results in center of the tracks on observable parts of the vehicle. This can also be seen in the position error metrics for TruthID 2 and 4. The tracker is able to estimate the dimensions of the object with about 0.3 meters accuracy for the vehicles ahead and behind the ego vehicle. Because of higher certainty defined for the vehicles' dimensions in the helperInitGGIWFilter function, the tracker does not collapse the length of these vehicles, even when the best-fit ellipse has a very low length. As the passing vehicle (TruthID 3) was observed on all dimensions, its dimensions are measured more accurately than the other vehicles. However, as the passing vehicle maneuvers with respect to the ego vehicle, the error in yaw estimate is higher.

The GM-PHD in this example uses a rectangular shaped target model and uses received measurements to evaluate expected measurements on the boundary of the target. This model helps the tracker estimate the shape and orientation more accurately. However, the process of evaluating expected measurements on the edges of a rectangular target is computationally more expensive.

OSPA Metric

As described earlier, the OSPA metric aims to describe the performance of a tracking algorithm using a single score. Notice that the OSPA sufficiently captures the performance of the tracking algorithm which decreases from GM-PHD to GGIW-PHD to the point-target tracker, as described using the error and assignment metrics.

ospaFig = figure;
plot(ospaMetric,'LineWidth',2);
legend('Point Target Tracker','GGIW-PHD Tracker','Rectangular GM-PHD Tracker');
xlabel('Time step (k)');
ylabel('OSPA');

Compare Time Performance

Previously, you learned about different techniques, the assumptions they make about target models, and the resulting tracking performance. Now compare the run-times of the trackers. Notice that GGIW-PHD filter offers significant computational advantages over the GM-PHD, at the cost of decreased tracking performance.

runTimeFig = figure;
h = plot(trackerRunTimes(3:end,:)./trackerRunTimes(3:end,1),'LineWidth',2);
legend('Point Target Tracker','GGIW-PHD Tracker','Rectangular GM-PHD Tracker');
xlabel('Time step (k)');
ylabel('$$\frac{t_{tracker}}{t_{multiObjectTracker}}$$','interpreter','latex','fontsize',14);
ylim([0 max([h.YData]) + 1]);

Summary

This example showed how to track objects that return multiple detections in a single sensor scan using different approaches. These approaches can be used to track objects with high-resolution sensors, such as a radar or laser sensor.

References

[1] Granström, Karl, Marcus Baum, and Stephan Reuter. "Extended Object Tracking: Introduction, Overview and Applications." Journal of Advances in Information Fusion. Vol. 12, No. 2, December 2017.

[2] Granström, Karl, Christian Lundquist, and Umut Orguner. "Tracking rectangular and elliptical extended targets using laser measurements." 14th International Conference on Information Fusion. IEEE, 2011.

[3] Granström, Karl. "Extended target tracking using PHD filters." 2012

Supporting Functions

helperExtendedTargetError

Function to define the error between tracked target and the associated ground truth.

function [posError,velError,dimError,yawError] = helperExtendedTargetError(track,truth)
% Errors as a function of target track and associated truth.

% Get true information from the ground truth.
truePos = truth.Position(1:2)';
% Position is at the rear axle for all vehicles. We would like to compute
% the error from the center of the vehicle
rot = [cosd(truth.Yaw) -sind(truth.Yaw);sind(truth.Yaw) cosd(truth.Yaw)];
truePos = truePos + rot*[truth.Wheelbase/2;0];

trueVel = truth.Velocity(1:2);
trueYaw = truth.Yaw(:);
trueDims = [truth.Length;truth.Width];

% Get estimated value from track. 
% GGIW-PHD tracker outputs a struct field 'Extent' and 'SourceIndex' 
% GM-PHD tracker outputs struct with but not 'Extent'
% multiObjectTracker outputs objectTrack

if isa(track,'objectTrack')
    estPos = track.State([1 3]);
    estVel = track.State([2 4]);
    % No yaw or dimension information in multiObjectTracker.
    estYaw = nan;
    estDims = [nan;nan];
elseif isfield(track,'Extent') % trackerPHD with GGIWPHD
    estPos = track.State([1 3]);
    estVel = track.State([2 4]);
    estYaw = atan2d(estVel(2),estVel(1));
    d = eig(track.Extent);
    dims = 2*sqrt(d);
    estDims = [max(dims);min(dims)];
else % trackerPHD with GMPHD
    estPos = track.State(1:2);
    estYaw = track.State(4);
    estVel = [track.State(3)*cosd(estYaw);track.State(3)*sind(estYaw)];
    estDims = track.State(6:7);
end

% Compute 2-norm of error for each attribute.
posError = norm(truePos(:) - estPos(:));
velError = norm(trueVel(:) - estVel(:));
dimError = norm(trueDims(:) - estDims(:));
yawError = norm(trueYaw(:) - estYaw(:));
end

helperExtendedTargetDistance

Function to define the distance between a track and a ground truth.

function dist = helperExtendedTargetDistance(track,truth)
% This function computes the distance between track and a truth.

% Copyright 2019-2020 The MathWorks, Inc.

% Errors in each aspect
[posError,velError,dimError,yawError] =  helperExtendedTargetError(track,truth);

% For multiObjectTracker, add a constant penalty for not estimating yaw
% and dimensions
if isnan(dimError)
    dimError = 1;
end
if isnan(yawError)
    yawError = 1;
end

% Distance is the sum of errors
dist = posError + velError + dimError + yawError;


end

helperInitGGIWFilter

Function to create a ggiwphd filter from a detection cell.

function phd = helperInitGGIWFilter(varargin)
% helperInitGGIWFilter A function to initialize the GGIW-PHD filter for the
% Extended Object Tracking example

% Create a ggiwphd filter using 5 states and the constant turn-rate models.
phd = ggiwphd(zeros(5,1),eye(5),...
    'StateTransitionFcn',@constturn,...
    'StateTransitionJacobianFcn',@constturnjac,...
    'MeasurementFcn',@ctmeas,...
    'MeasurementJacobianFcn',@ctmeasjac,...
    'HasAdditiveMeasurementNoise',true,...
    'HasAdditiveProcessNoise',false,...
    'ProcessNoise',diag([1 1 3]),...
    'MaxNumComponents',1000,...
    'ExtentRotationFcn',@extentRotFcn,...
    'PositionIndex',[1 3]);

% If the function is called with no inputs i.e. the predictive portion of
% the birth density, no components are added to the mixture.
if nargin == 0
    % Nullify to return 0 components.
    nullify(phd);
else
    % When called with detections input, add two components to the filter,
    % one for car and one for truck, More components can be added based on
    % prior knowledge of the scenario, example, pedestrian or motorcycle.
    % This is a "multi-model" type approach. Another approach can be to add
    % only 1 component with a higher covariance in the dimensions. The
    % later is computationally less demanding, but has a tendency to track
    % observable dimensions of the object. For example, if only the back is
    % visible, the measurement noise may cause the length of the object to
    % shrink.
    
    % Detections
    detections = varargin{1};
    
    % Enable elevation measurements to create a 3-D filter using
    % initctggiwphd
    if detections{1}.SensorIndex < 7
        for i = 1:numel(detections)
            detections{i}.Measurement = [detections{i}.Measurement(1);0;detections{i}.Measurement(2:end)];
            detections{i}.MeasurementNoise = blkdiag(detections{i}.MeasurementNoise(1,1),0.4,detections{i}.MeasurementNoise(2:end,2:end));
            detections{i}.MeasurementParameters(1).HasElevation = true;
        end
    end
    phd3d = initctggiwphd(detections);
    
    % Set states of the 2-D filter using 3-D filter
    phd.States = phd3d.States(1:5);
    phd.StateCovariances = phd3d.StateCovariances(1:5,1:5);
    
    phd.DegreesOfFreedom = 1000;
    phd.ScaleMatrices = (1000-4)*diag([4.7/2 1.8/2].^2);
    
    % Add truck dimensions as second component
    append(phd,phd);
    phd.ScaleMatrices(:,:,2) = (1000-4)*diag([8.1/2 2.45/2].^2);
    phd.GammaForgettingFactors = [1.03 1.03];
    
    % Relative weights of the components. Can be treated as probability of
    % existence of a car vs a truck on road.
    phd.Weights = [0.7 0.3];
end
end

function R = extentRotFcn(x,dT)
    % Rotation of the extent during prediction.
    w = x(5);
    theta = w*dT;
    R = [cosd(theta) -sind(theta);sind(theta) cosd(theta)]; 
end

helperInitRectangularFilter

Function to create a gmphd rectangular target filter from a detection cell.

function filter = helperInitRectangularFilter(varargin)
% helperInitRectangularFilter A function to initialize the rectangular
% target PHD filter for the Extended Object Tracking example

% Copyright 2019 The MathWorks, Inc.

if nargin == 0
    % If called with no inputs, simply use the initctrectgmphd function to
    % create a PHD filter with no components.
    filter = initctrectgmphd;
    % Set process noise
    filter.ProcessNoise = diag([1 3]);
else
    % When called with detections input, add two components to the filter,
    % one for car and one for truck, More components can be added based on
    % prior knowledge of the scenario, example, pedestrian or motorcycle.
    % This is a "multi-model" type approach. Another approach can be to add
    % only 1 component with a higher covariance in the dimensions. The
    % later is computationally less demanding, but has a tendency to track
    % observable dimensions of the object. For example, if only the back is
    % visible, the measurement noise may cause the length of the object to
    % shrink.
    
    % Detections
    detections = varargin{1};
    
    % Create a GM-PHD filter with rectangular model
    filter = initctrectgmphd(detections);
    
    % Length width of a passenger car
    filter.States(6:7,1) = [4.7;1.8];
    
    % High certainty in dimensions
    lCov = 1e-4;
    wCov = 1e-4;
    lwCorr = 0.5;
    lwCov = sqrt(lCov*wCov)*lwCorr;
    filter.StateCovariances(6:7,6:7,1) = [lCov lwCov;lwCov wCov];
    
    % Add one more component by appending the filter with itself.
    append(filter,filter);
    
    % Set length and width to a truck dimensions
    filter.States(6:7,2) = [8.1;2.45];
    
    % Relative weights of each component
    filter.Weights = [0.7 0.3];
end

end