本页采用了机器翻译。点击此处可查看最新英文版本。

比较替代优化与其他求解器

打开实时脚本

此示例将 surrogateopt 与另外两个求解器进行比较：fmincon（推荐用于平滑问题的求解器）和 patternsearch（推荐用于非平滑问题的求解器）。该示例在二维区域上使用非光滑函数。

type nonSmoothFcn
function [f, g] = nonSmoothFcn(x)
%NONSMOOTHFCN is a non-smooth objective function

%   Copyright 2005 The MathWorks, Inc.

for i = 1:size(x,1)
    if  x(i,1) < -7
        f(i) = (x(i,1))^2 + (x(i,2))^2 ;
    elseif x(i,1) < -3
        f(i) = -2*sin(x(i,1)) - (x(i,1)*x(i,2)^2)/10 + 15 ;
    elseif x(i,1) < 0
        f(i) = 0.5*x(i,1)^2 + 20 + abs(x(i,2))+ patho(x(i,:));
    elseif x(i,1) >= 0
        f(i) = .3*sqrt(x(i,1)) + 25 +abs(x(i,2)) + patho(x(i,:));
    end
end

%Calculate gradient
g = NaN;
if x(i,1) < -7
    g = 2*[x(i,1); x(i,2)];
elseif x(i,1) < -3
    g = [-2*cos(x(i,1))-(x(i,2)^2)/10; -x(i,1)*x(i,2)/5];
elseif x(i,1) < 0
    [fp,gp] = patho(x(i,:));
    if x(i,2) > 0
        g = [x(i,1)+gp(1); 1+gp(2)];
    elseif x(i,2) < 0
        g =  [x(i,1)+gp(1); -1+gp(2)];
    end
elseif x(i,1) >0
    [fp,gp] = patho(x(i,:));
    if x(i,2) > 0
        g = [.15/sqrt(x(i,1))+gp(1); 1+ gp(2)];
    elseif x(i,2) < 0
        g = [.15/sqrt(x(i,1))+gp(1); -1+ gp(2)];
    end
end

function [f,g] = patho(x)
Max = 500;
f = zeros(size(x,1),1);
g = zeros(size(x));
for k = 1:Max  %k 
   arg = sin(pi*k^2*x)/(pi*k^2);
   f = f + sum(arg,2);
   g = g + cos(pi*k^2*x);
end

mplier = 0.1; % Scale the control variable
Objfcn = @(x)nonSmoothFcn(mplier*x); % Handle to the objective function
range = [-6 6;-6 6]/mplier; % Range used to plot the objective function
rng default % Reset the global random number generator
showNonSmoothFcn(Objfcn,range);
title('Nonsmooth Objective Function')
view(-151,44)

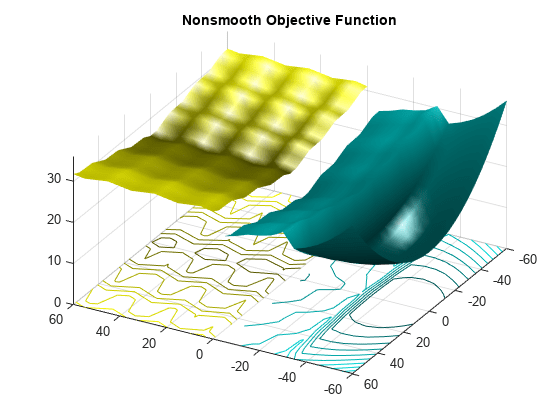
Figure contains an axes object. The axes object with title Nonsmooth Objective Function contains 4 objects of type surface, contour.

drawnow

看看 surrogateopt 在默认迭代次数内定位全局最小值的表现如何。

lb = -6*ones(1,2)/mplier;
ub = -lb;
[xs,fvals,eflags,outputs] = surrogateopt(Objfcn,lb,ub);

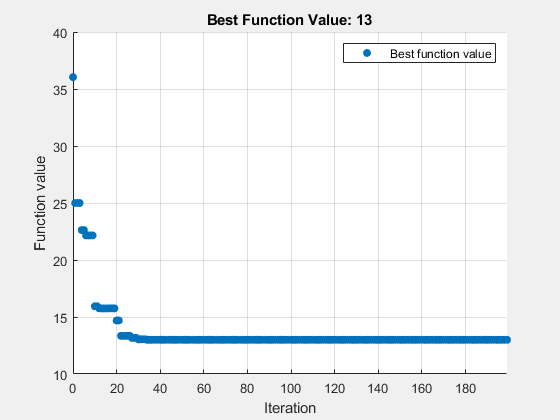
Figure Optimization Plot Function contains an axes object. The axes object with title Best Function Value: 13, xlabel Iteration, ylabel Function value contains an object of type scatter. This object represents Best function value.

surrogateopt stopped because it exceeded the function evaluation limit set by 
'options.MaxFunctionEvaluations'.

fprintf("Lowest found value = %g.\r",fvals)
Lowest found value = 13.

figure
showNonSmoothFcn(Objfcn,range);
view(-151,44)
hold on
p1 = plot3(xs(1),xs(2),fvals,'om','MarkerSize',15,'MarkerFaceColor','m');
legend(p1,{'Solution'})
hold off

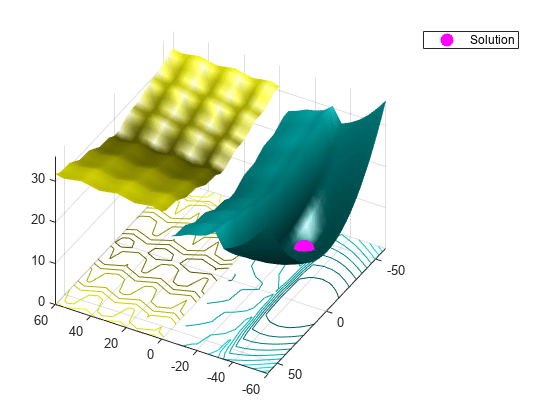
Figure contains an axes object. The axes object contains 5 objects of type surface, contour, line. One or more of the lines displays its values using only markers This object represents Solution.

与 patternsearch 比较

设置 patternsearch 选项以使用相同数量的函数计算，从边界内的随机点开始。

rng default
x0 = lb + rand(size(lb)).*(ub - lb);
optsps = optimoptions('patternsearch','MaxFunctionEvaluations',200,'PlotFcn','psplotbestf');
[xps,fvalps,eflagps,outputps] = patternsearch(Objfcn,x0,[],[],[],[],lb,ub,[],optsps);
patternsearch stopped because the mesh size was less than options.MeshTolerance.

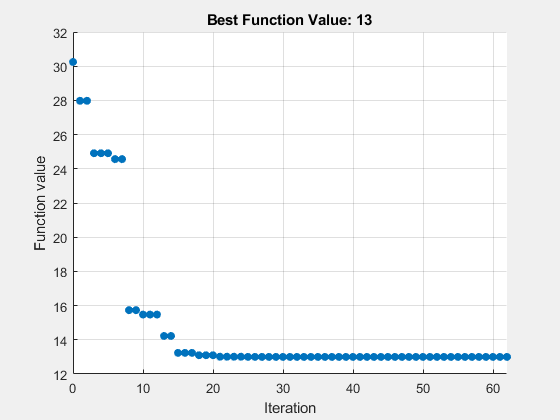
Figure Pattern Search contains an axes object. The axes object with title Best Function Value: 13, xlabel Iteration, ylabel Function value contains an object of type scatter.

figure
showNonSmoothFcn(Objfcn,range);
view(-151,44)
hold on
p1 = plot3(x0(1),x0(2),Objfcn(x0),'ob','MarkerSize',12,'MarkerFaceColor','b');
p2 = plot3(xps(1),xps(2),fvalps,'om','MarkerSize',15,'MarkerFaceColor','m');
legend([p1,p2],{'Start Point','Solution'})
hold off

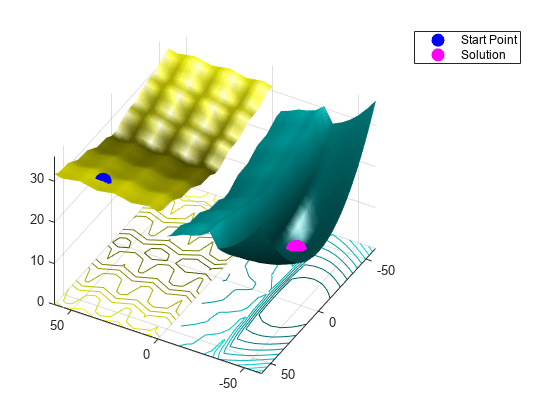
Figure contains an axes object. The axes object contains 6 objects of type surface, contour, line. One or more of the lines displays its values using only markers These objects represent Start Point, Solution.

patternsearch 找到了与 surrogateopt 相同的解。

限制函数计算的次数并重试。

optsurr = optimoptions('surrogateopt','MaxFunctionEvaluations',40);
[xs,fvals,eflags,outputs] = surrogateopt(Objfcn,lb,ub,optsurr);

Figure Optimization Plot Function contains an axes object. The axes object with title Best Function Value: 13.0003, xlabel Iteration, ylabel Function value contains an object of type scatter. This object represents Best function value.

surrogateopt stopped because it exceeded the function evaluation limit set by 
'options.MaxFunctionEvaluations'.

optsps.MaxFunctionEvaluations = 40;
[xps,fvalps,eflagps,outputps] = patternsearch(Objfcn,x0,[],[],[],[],lb,ub,[],optsps);
patternsearch stopped because it exceeded options.MaxFunctionEvaluations.

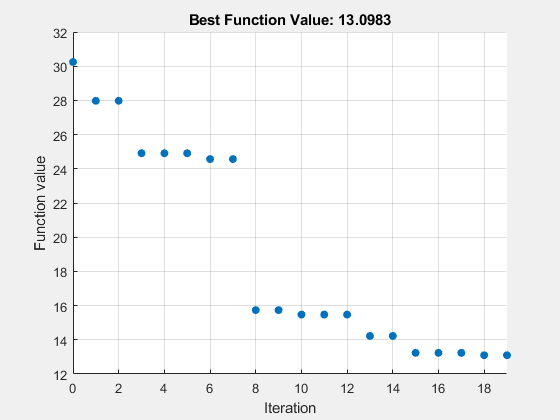
Figure Pattern Search contains an axes object. The axes object with title Best Function Value: 13.0983, xlabel Iteration, ylabel Function value contains an object of type scatter.

再次，两个求解器都快速找到了全局解。

与 fmincon 比较

fmincon 能够有效地在起点附近找到局部解。然而，在非凸或非光滑问题中，它很容易远离全局解。

设置 fmincon 选项以使用绘图函数、与之前的求解器相同数量的函数计算以及与 patternsearch 相同的起点。

opts = optimoptions('fmincon','PlotFcn','optimplotfval','MaxFunctionEvaluations',200);
[fmsol,fmfval,eflag,fmoutput] = fmincon(Objfcn,x0,[],[],[],[],lb,ub,[],opts);

Figure Optimization Plot Function contains an axes object. The axes object with title Current Function Value: 30.1703, xlabel Iteration, ylabel Function value contains an object of type scatter.

Local minimum possible. Constraints satisfied.

fmincon stopped because the size of the current step is less than
the value of the step size tolerance and constraints are 
satisfied to within the value of the constraint tolerance.

<stopping criteria details>

figure
showNonSmoothFcn(Objfcn,range);
view(-151,44)
hold on
p1 = plot3(x0(1),x0(2),Objfcn(x0),'ob','MarkerSize',12,'MarkerFaceColor','b');
p2 = plot3(fmsol(1),fmsol(2),fmfval,'om','MarkerSize',15,'MarkerFaceColor','m');
legend([p1,p2],{'Start Point','Solution'})
hold off

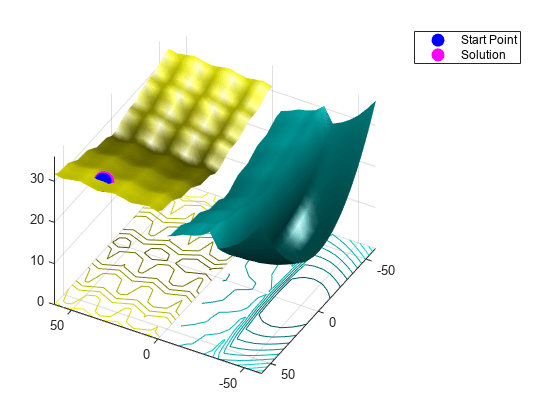
Figure contains an axes object. The axes object contains 6 objects of type surface, contour, line. One or more of the lines displays its values using only markers These objects represent Start Point, Solution.

fmincon 陷入了起点附近的局部最小值。

另请参阅

| |

主题