使用多目标优化规划核燃料处置
此示例说明如何制定和解决具有一些整数约束的大型非线性多目标问题。该问题改编自 Montonen、Ranta 和 Mäkelä [1]。其目的是处理废核燃料,目标是尽量减少成本,尽量减少从反应堆中取出废核燃料组件到埋藏之间的时间,并尽量减少任何时候储存的废燃料组件数量。该问题是一个多期规划问题,每个期为五年。
模型概述
核反应堆产生的废物必须进行长期掩埋处置。这些废品是含有废核燃料的燃料棒组件。从反应堆中取出时,组件很热且具有放射性,但放射性会逐渐降低。在周期 t,辐射水平由参数向量 u 的双指数衰减函数给出:
.
每个组件都留在反应堆建筑物的水池中,直到冷却到可以转移到临时存储设施中,然后再放入水池中。当组件进一步冷却后,可以将其与其他组件一起封装在铜铁罐中,然后埋在处置隧道中。所有处置隧道均连接至中央隧道。
该图说明了核燃料组件从反应堆到最终处置的各个阶段。
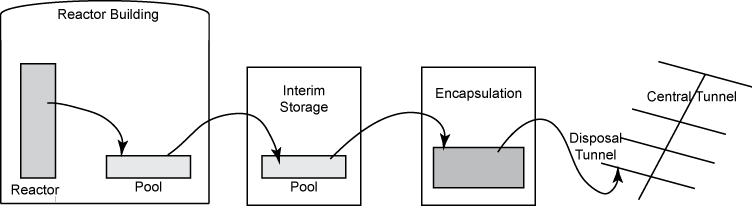
问题变量与每个时间单位代表 5 年的时间表有关。时间段从 1 开始。
与模型相关的常量
Z 是燃料组件从反应堆中删除的最后时间段。删除时间段为 1:Z。在 [1] 中,Z = 11。每个时期为 5 年,因此最后一个拆除燃料组件的时期是时间 55。
N 是最后埋藏毒罐的时间段。埋藏时期为 1:N。在 [1] 中,N = 19。每个时期为 5 年,因此最后一个可以埋葬罐子的时期是时间 95。
Z = 11; N = 19;
a 是第一次处置之前最后一次拆除的时期。
b 是最后一次删除发生的处置期。
a = 5; b = 6;
R 是存储组件的最小周期数。
R = 4;
K 是一个罐中可容纳的最大组件数量。
K = 4;
T 是一段时期内处理的最少罐数。
T = 50;
U 是一段时期内处理的最大罐数。
U = 500;
Q 是处置隧道的长度(以米为单位)。
Q = 350;
M(i) 是在时间 i 时删除的程序集数量。
M = 300 - 60*(-1).^(1:Z); % 360 for odd indices, 240 for evenA(i,j) 是从 i 删除的组件在 j 周期内的存储时间,其中 i <= Z 和 j <= N。
A = zeros(Z,N); for i = 1:Z for j = i:N A(i, j) = j - i; end end
p(i,j) 是组件在 i 周期内从 j 删除而产生的衰变热功率(以瓦特为单位),其中 i <= Z 和 j <= N。
% The following parameters fit P_{i,j} of Table A2 from [1] to within 1 in each % entry (fractional error <= 1/250). u = [503 0.1346 260 0.0231]; myfun = @(d)round(u(1)*exp(-u(2)*d) + u(3)*exp(-u(4)*d)); PP = myfun(1:N); pij = zeros(Z,N); for i = 2:Z for j = 1:i pij(i,j) = 1e3; % Dummy values because j >= i does not occur. end end for i=1:Z pij(i,i:end) = PP(1:(N-i+1)); % Same decay profile for all removal times end
pmaxup 是罐体平均功率的上界,pmaxlow 是下界。
pmaxup = 1830; pmaxlow = 1300;
dDTup 是处置隧道之间距离的上界,dDTlow 是下界。
dDTup = 50; dDTlow = 25;
dCAup 是处置隧道中罐子之间距离的上界,dCAlow 是下界。
dCAup = 15; dCAlow = 6;
[1]中没有给出与这些操作相关的成本。此示例假设以下值:
Cas是每期间一个组件的存储成本。Cis是临时存储中每个期间一个组件的存储成本。Csp是每个组件的存储空间成本。Cca是罐子的成本。Cef是每个时期封装设施的运行成本。Cdt是每米处置隧道的成本。Cct是中央隧道每米的成本。
Cas = 50; Cis = 60; Csp = 10; Cca = 1200; Cef = 300; Cdt = 3000; Cct = 5000;
问题的优化变量
要为 MATLAB® 创建问题,请使用基于问题的方法。为大多数数量定义连续变量。
该图说明了与组件移动相关的变量。

x(i,j) 是在时间 i 删除并在时间 j、i <= Z 和 j <= N 处置的程序集的数量。
x = optimvar("x",Z,N,LowerBound=0,UpperBound=U*K);z(i,j) 是在时间 i 删除并在时间 j、i <= Z 和 j <= N 存储的程序集的数量。
z = optimvar("z",Z,N,LowerBound=0,UpperBound=U*K*N/2);y(j) 是在 j <= N 时刻处理的罐子数量。
y = optimvar("y",N,LowerBound=0,UpperBound=U);pmax 是罐的最大平均功率。
pmax = optimvar("pmax",LowerBound=pmaxlow,UpperBound=pmaxup);该图显示了与处置隧道相关的数量。
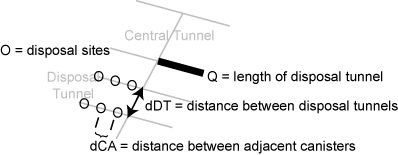
dDT 是相邻处置隧道之间的距离。
dDT = optimvar("dDT",LowerBound=dDTlow,UpperBound=dDTup);dCA 是处置隧道中相邻罐之间的距离。稍后您将在此示例的问题约束部分使用函数 g 计算该距离。
该数字与封装时间有关。

将以下变量指定为整数类型二进制变量,其下界为 0,上界为 1。
ej(j) 表示封装设施在 j <= N 期间处于运行状态。
ej = optimvar("ej",N,Type="integer",LowerBound=0,UpperBound=1);
ejON(j) 表示封装从 j <= N 周期开始。
ejON = optimvar("ejON",N,Type="integer",LowerBound=0,UpperBound=1);
ejOFF(j) 表示封装在 j <= N 周期开始时结束。
ejOFF = optimvar("ejOFF",N,Type="integer",LowerBound=0,UpperBound=1);
这个数字与可以处置程序集的时间有关,rij = 1。这些时间从 ejON = 1 开始,到 sij = 1 结束。

sij(i,j) 表示在时间 i 删除的程序集从时间 j、i <= Z 和 j <= N 开始无法再被处置。
sij = optimvar("sij",Z,N,Type="integer",LowerBound=0,UpperBound=1);
rij(i,j) 表示在时间 i 删除的程序集可以在时间 j、i <= Z 和 j <= N 处处置。
rij = optimvar("rij",Z,N,Type="integer",LowerBound=0,UpperBound=1);
现在所有优化变量和问题参数都已定义。
问题约束
创建一个优化问题来满足目标和约束。
prob = optimproblem;
约束数字与 [1] 中的方程相匹配。前三个约束与临时存储中的组件数量有关。
jnot1 = 2:N; prob.Constraints.cons10 = z(:,1) - M(:) + x(:,1) == 0; prob.Constraints.cons11 = z(:,jnot1) - z(:,(jnot1 - 1)) + x(:,jnot1) == 0; prob.Constraints.cons12 = z(:,N) == 0;
设置所有程序集均一次性处置的约束。
prob.Constraints.cons13 = sum(sij,2) == 1;
通过设置以下约束来定义变量 rij。
cons15 = optimconstr(Z,N); cons15(:,1) = rij(:,1) == -sij(:,1) + ejON(1); % equation 14 cons15(:,jnot1) = rij(:,jnot1) == ... rij(:,jnot1-1) - sij(:,jnot1) + repmat(ejON(jnot1)',Z,1); % equation 15 prob.Constraints.cons15 = cons15;
设置仅在封装设施运行期间进行处置的约束。
cons16 = rij <= repmat(ej', Z, 1); prob.Constraints.cons16 = cons16;
指定不超出生产能力的约束。
prob.Constraints.cons17 = x <= U*K*rij;
下一个约束要求组件在处置之前必须足够冷。
prob.Constraints.cons18 = x.*(A - R) >= 0;
以下约束与封装设施有关。这些约束强制要求设施只能打开和关闭一次,这意味着所有的罐子都在一次运行中被封装起来,
prob.Constraints.cons19 = sum(ejON) == 1; prob.Constraints.cons20 = sum(ejOFF) == 1;
通过设置以下约束来定义变量 ej。
cons21 = optimconstr(N); cons21(1) = ej(1) == ejON(1) - ejOFF(1); % equation 21 cons21(jnot1) = ej(jnot1) == ... ej(jnot1 - 1) + ejON(jnot1) - ejOFF(jnot1); % equation 22 prob.Constraints.cons21 = cons21;
设定约束:罐数足够处置、不超过生产能力、并遵守最小生产约束。
prob.Constraints.cons23 = y' >= (1/K)*sum(x,1); prob.Constraints.cons24 = y <= U*ej; jnotN = 1:(N-1); prob.Constraints.cons25 = y(jnotN) >= T*(ej(jnotN) - ejOFF(jnotN + 1));
对于处置设施,设定了允许罐体热功率的约束。
prob.Constraints.cons26 = sum(pij.*x,1) <= pmax*y';
对埋置罐之间的距离指定非线性约束。该函数是分段线性的,使用 max 函数定义,这不是优化表达式支持的操作。因此,使用 fcn2optimexpr 将约束放入 prob 中。
g = @(pmax,dDT)max([-2.26911*dDT + 0.00675*pmax + 54.5288,... -0.05833*dDT + 0.00596*pmax - 0.727083,... -0.14*dDT + 0.17701*pmax - 350.651]); dCA = fcn2optimexpr(@(pmax,dDT)g(pmax,dDT),pmax,dDT); prob.Constraints.cons29a = dCA >= dCAlow; prob.Constraints.cons29b = dCA <= dCAup;
成本目标
这个多目标问题的第一个目标是成本,它有七个分量。
cost = optimexpr(7,1);
1.组件的存储成本。该成本是单位时间成本乘以每个组件存储时间长度的总和。
cost(1) = Cas*sum(A.*x,"all");2.临时存储成本。对于 j*ejOFF(j) 的一个分量 ejOFF 来说,这个成本是 1。
cost(2) = Cis*max(ejOFF(1)–1,2*ejOFF(2)–1,3*ejOFF(3)–1,...,N*ejOFF(N)–1).
为了简要地表示这个表达式,将 cost(2) = Cis*u 表示为一个新的优化变量 u,以及约束
ucons = u >= ((1:N)'.*ejOFF) – 1.
u = optimvar("u",LowerBound=0);
cost(2) = Cis*u;
ucons = u >= ((1:N)'.*ejOFF) - 1;
prob.Constraints.ucons = ucons;3.装配存储位置成本。cost(3) 可以用 Csp*v1 表示,其中 v1 是一个新的优化变量,以及约束
v1 >= sum(M)
每个 1 <= j <= N(用于每个 v1 >= sum_{i=1}^j z(i,j))
每个 b <= j <= N(用于每个 v1 >= sum_{i=1}^Z z(i,j))。
创建这些成本和相关约束。
v1 = optimvar("v1",LowerBound=0); cost(3) = Csp*v1; % Include the three v1 constraints given below. v1consa = v1 >= sum(M); bmin1 = 1:(b-1); v1consb = optimconstr(b-1); for j=bmin1 v1consb(j) = sum(z(1:a+j,j)) <= v1; end ell = b:N; v1consc = sum(z(:,ell),1) <= v1; prob.Constraints.v1consa = v1consa; prob.Constraints.v1consb = v1consb; prob.Constraints.v1consc = v1consc;
4.罐子的成本。该成本等于每个罐的成本乘以埋藏的罐总数。
cost(4) = Cca*sum(y);
5.运行封装设施的成本。该成本是单位时间成本乘以设施运行的时间长度。
cost(5) = Cef*sum(ej);
6.处置隧道的成本。这是每单位长度的成本乘以罐之间的长度乘以埋藏的罐总数。
cost(6) = Cdt*dCA*sum(y);
7.中央隧道的成本。该成本是每单位长度的成本乘以中央隧道所需长度。一条处置隧道内可埋置的罐子数量等于隧道长度 Q 除以罐子之间的距离 dCA。中央隧道的长度与埋藏的罐子的数量 sum(y) 成正比,与 Q/dCA 成反比,成本与 Cct 成正比。
cost(7) = Cct/Q*dDT*dCA*sum(y);
总成本是七个成本分量的总和。为了改变总成本的规模来匹配其他目标的规模,请对总和取对数。
prob.Objective.cost = log(sum(cost));
安全目标
该问题有两个与安全相关的目标。目标 2,名为 safety1,试图最小化所有删除的最大存储时间。目标 3,名为 safety2,尝试尽早停止处置。使用辅助函数 max1 和 max2 定义这两个目标,它们出现在此脚本的末尾。
prob.Objective.safety1 = fcn2optimexpr(@max1,A,sij); % Minimize maximum storage time, objective (2) in [1] prob.Objective.safety2 = fcn2optimexpr(@max2,ejOFF); % Stop disposal as early as possible, objective (5) in [1]
设置选项
随着求解器的进行,设置帕累托图的选项。由于问题有超过 900 个变量,因此设置选项以使用 500 的种群规模,这大于默认值。此外,由于问题包含二进制变量,因此请使用 mutationgaussian 变异函数。对于二元变量来说,此变异函数比默认的 mutationpower 效果更好。
opts = optimoptions("gamultiobj",PlotFcn="gaplotpareto",PopulationSize=5e2,... MutationFcn=@mutationgaussian);
运行问题
问题表述已完成,并且为该多目标问题设置了选项。运行问题。
rng default % For reproducibility [sol,fval,exitflag,output] = solve(prob,Options=opts);
Solving problem using gamultiobj. gamultiobj stopped because the average change in the spread of Pareto solutions is less than options.FunctionTolerance.
xlabel("Cost") ylabel("Safety 1") zlabel("Safety 2")
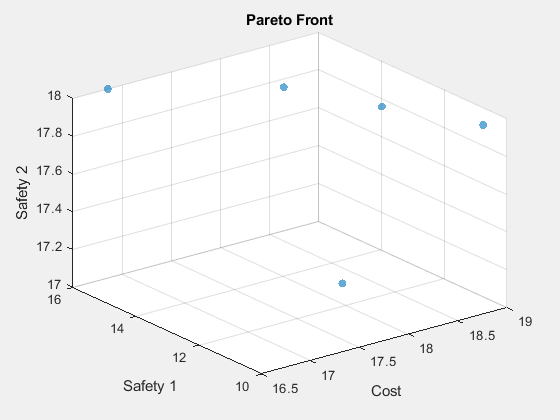
帕累托图显示了成本和安全性 1 之间的明显权衡。真实成本是所示金额的指数,因此权衡比所示的更为严重。
检查解
gamultiobj 找到了几个具有不同适应度函数值的可行解。要找到与解相关的控制变量,请使用数据提示。

激活数据提示后,点击左上角的解。要查看数据提示,您可能需要使用以下命令:
ax = gca;
ax.Clipping = "off";
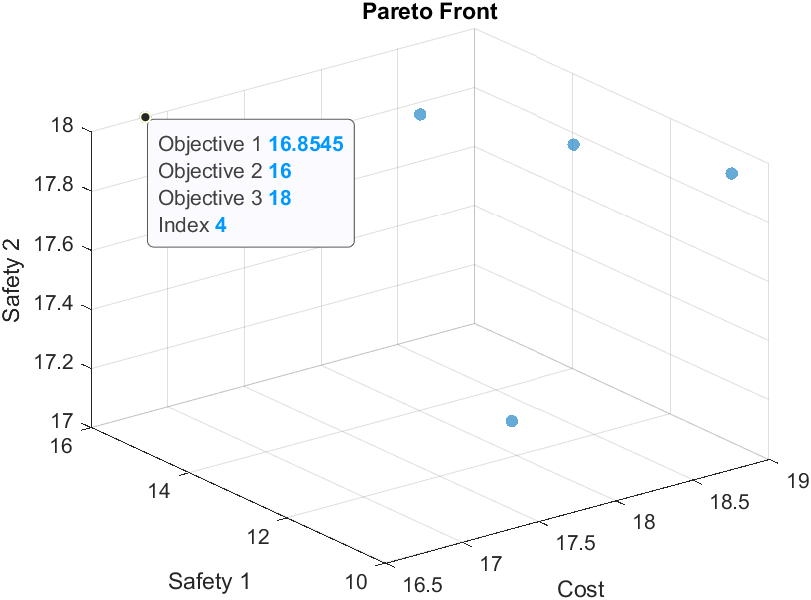
选定点的索引为 8。与该点相关的变量在 sol(3) 中。
检查与此解相关的 x 变量。回想一下,x(i,j) 是在时间 i 时删除的,并在时间 j 时处理掉。
disp(sol(8).x)
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 360 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 240 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 360 0
0 0 0 0 0 0 0 0 0 0 0 0 0 240 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 360 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 240 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 360 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 240 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 360 0
0 0 0 0 0 0 0 0 0 0 0 0 0 240 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 360 0 0 0 0
解是整数值。查看 x 处置计划的总和与 M(:) 清除量相比的情况。
disp([sum(sol(3).x,2),M(:)])
360 360 240 240 360 360 240 240 360 360 240 240 360 360 240 240 360 360 240 240 360 360
x 计划考虑了所有删除。
封装设施的运行时间是什么时候?
disp(sol(8).ej')
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0
封装运行次数为 14 至 18。
处置隧道之间的距离是多少?
disp(sol(8).dDT)
33.4536
距离约为下界 25 米与上界 50 米的中间点。
该计划的美元成本是多少?为了找出答案,计算 exp(sol(4).cost),因为 sol(4).cost 是总处置成本的对数。
disp(exp(sol(8).cost))
3.1936e+07
成本约为 3200 万美元。
检查帕累托集中目标 2 值最低的点。
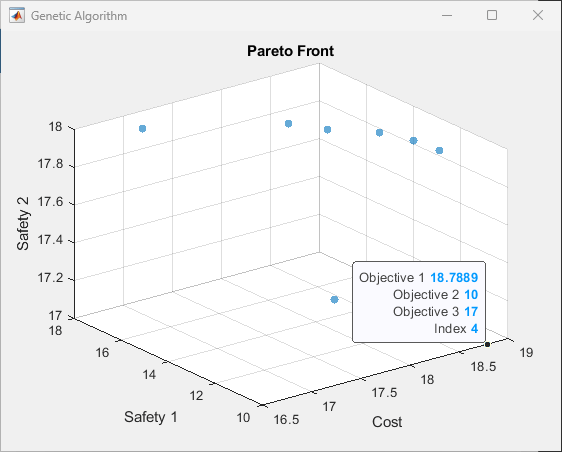
该点的索引为 10。这个操作点的货币成本要高得多。
disp(exp(sol(10).cost))
1.2827e+08
货币成本约为 1.28 亿美元,是之前价值的四倍以上。但好处是,目标 2 从 17 减少到 9,这相当于提前 40 年(=8*5)减少了废物埋葬量。越早埋葬越安全。
查看此解的 x 的时间表。
disp(sol(10).x)
0 0 0 0 0 360.0000 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 240.0000 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 360.0000 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 240.0000 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 360.0000 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 240.0000 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 360.0000 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 18.4809 37.6345 0 183.8847 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 360.0000 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 240.0000 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 360.0000 0 0 0 0
这些解并非都是整数值。查看 x 处置计划的总和与 M(:) 清除量相比的情况。
disp([sum(sol(4).x,2),M(:)])
360 360 240 240 360 360 240 240 360 360 240 240 360 360 240 240 360 360 240 240 360 360
再次强调,该计划记录了所有拆除情况。
封装设施的运行时间是什么时候?
disp(sol(10).ej')
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0
封装运行次数为 1 至 16。
该解的处置隧道之间的距离是多少?
disp(sol(10).dDT)
25
这次,下界的距离为 25 米。
结论
此示例展示了使用基于问题的方法制定非线性、多目标、混合整数优化问题。帕累托图中的数据提示使您能够分析解。您无需指定 gaplotpareto 绘图函数,而是可以使用 paretoplot函数从解中获取类似的绘图。
参考资料
[1] Montonen, Outi, Timo Ranta, and Marko M. Mäkelä.Planning the Schedule for the Disposal of the Spent Nuclear Fuel with Interactive Multiobjective Optimization.Algorithms Vol. 12, Issue 12, 2019.Available at https://www.mdpi.com/1999-4893/12/12/252.
辅助函数
以下代码创建 max1 辅助函数。
function v = max1(A,sij) v = round(max(max(A.*sij - 1))); % "round" ensures integer values end
以下代码创建 max2 辅助函数。
function v = max2(ejOFF) v = round(max((ejOFF').*(1:length(ejOFF)) - 1)); end
另请参阅
gamultiobj | solve | paretoplot | paretosearch