设置最大代数和停滞代数
MaxGenerations 选项确定遗传算法任务接受的最大代数;请参阅算法的停止条件。增大 MaxGenerations 可以改进最终结果。相关的 MaxStallGenerations 选项控制 ga 经过的步骤数,查看是否有进展。增大 MaxStallGenerations 可以使 ga 在算法需要更多函数计算以求更优解时继续运行。
例如,使用具有默认参数的 10 个变量来优化 rastriginsfcn。要观察求解器在接近最小值 0 时的进展,请对函数的对数进行优化。
rng default % For reproducibility fun = @(x)log(rastriginsfcn(x)); nvar = 10; options = optimoptions('ga','PlotFcn',"gaplotbestf"); [x,fval] = ga(fun,nvar,[],[],[],[],[],[],[],options)
ga stopped because the average change in the fitness value is less than options.FunctionTolerance.
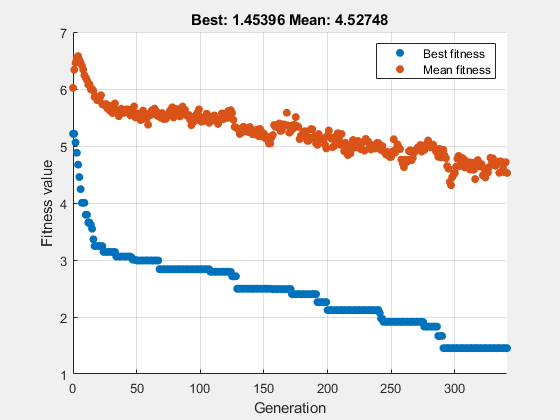
x = 1×10
-0.0495 -0.0670 -0.0485 0.0174 -0.0087 0.0275 -0.0383 0.0620 -1.0047 -0.0298
fval = 1.4540
当 ga 接近位于原点的最优点时,它会停滞。要获得更优解,请将停滞代数限值设置为 500,将代数限值设置为 1000。
options = optimoptions(options,'MaxStallGenerations',500,'MaxGenerations',1000); rng default % For reproducibility [x,fval] = ga(fun,nvar,[],[],[],[],[],[],[],options)
ga stopped because it exceeded options.MaxGenerations.
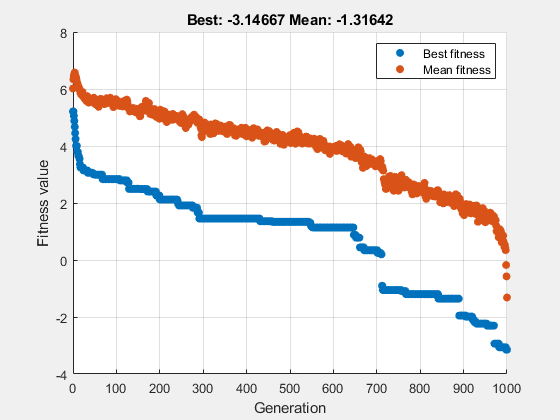
x = 1×10
0.0025 -0.0039 0.0021 -0.0030 -0.0053 0.0033 0.0080 0.0012 0.0006 0.0088
fval = -3.1467
这一次,求解器更加逼近真正的最小值。