使用 surrogateopt 优化多维函数,基于问题
此示例展示了如何在基于问题的方法中使用替代优化来最小化多维函数。要最小化的函数 multirosenbrock(x) 出现在此示例的末尾。multirosenbrock 函数在点 0 处具有 [1,1,...,1] 的单个局部最小值。该函数的设计对于求解器来说具有挑战性。
注意:multirosenbrock 辅助函数的代码在本示例末尾提供。确保代码包含在脚本末尾或路径上的文件中。
创建一个 4-D 优化变量 x。multirosenbrock 函数期望变量为行向量,因此将 x 指定为 4 元素行向量。
x = optimvar("x",1,4);surrogateopt 求解器要求所有问题变量都有有限的边界。指定下界为 -3,上界为 3。当您指定标量边界时,它们适用于所有问题变量。
x.LowerBound = -3; x.UpperBound = 3;
要使用 multirosenbrock 作为目标函数,请使用 fcn2optimexpr 将该函数转换为优化表达式。
fun = fcn2optimexpr(@multirosenbrock,x);
用目标函数 multirosenbrock 创建一个优化问题。
prob = optimproblem("Objective",fun);求解问题,指定 surrogateopt 求解器。
rng default % For reproducibility [sol,fval] = solve(prob,"Solver","surrogateopt")
Solving problem using surrogateopt.
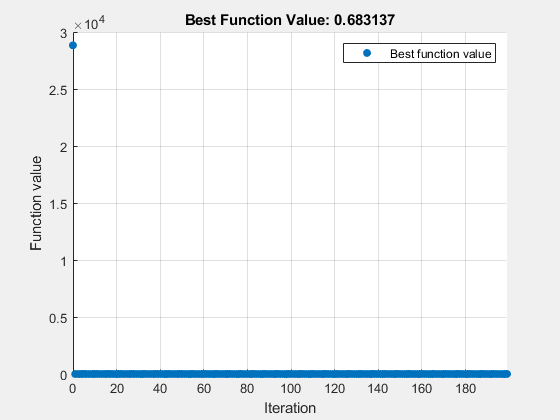
surrogateopt stopped because it exceeded the function evaluation limit set by 'options.MaxFunctionEvaluations'.
sol = struct with fields:
x: [0.2895 0.0882 0.5829 0.3348]
fval = 0.6831
尝试改进解
返回的解并不好,因为目标函数值不太接近 0。尝试通过运行 surrogateopt 进行更多评估来改进解。使用先前的解作为起点。
options = optimoptions("surrogateopt","MaxFunctionEvaluations",1000); [sol2,fval2] = solve(prob,sol,"Solver","surrogateopt","Options",options)
Solving problem using surrogateopt.
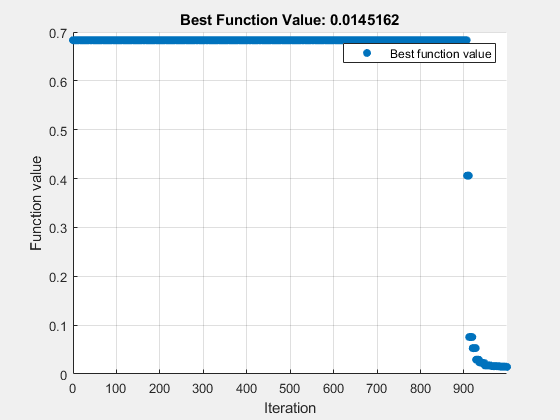
surrogateopt stopped because it exceeded the function evaluation limit set by 'options.MaxFunctionEvaluations'.
sol2 = struct with fields:
x: [1.0410 1.0844 0.8870 0.7865]
fval2 = 0.0145
这一次,求解器找到了一个很好的解。
辅助函数
以下代码创建 multirosenbrock 辅助函数。
function F = multirosenbrock(x) % This function is a multidimensional generalization of Rosenbrock's % function. It operates in a vectorized manner, assuming that x is a matrix % whose rows are the individuals. % Copyright 2014 by The MathWorks, Inc. N = size(x,2); % assumes x is a row vector or 2-D matrix if mod(N,2) % if N is odd error('Input rows must have an even number of elements') end odds = 1:2:N-1; evens = 2:2:N; F = zeros(size(x)); F(:,odds) = 1-x(:,odds); F(:,evens) = 10*(x(:,evens)-x(:,odds).^2); F = sum(F.^2,2); end
另请参阅
surrogateopt | fcn2optimexpr | solve