Spool Orifice (IL)

Variable-area spool orifice in an isothermal liquid system

Since R2020a

Libraries:
Simscape / Fluids / Isothermal Liquid / Valves & Orifices / Orifices

Description

The Spool Orifice (IL) block models a variable-area orifice between a spool and a sleeve with holes. The sleeve holes can be either a series of round or rectangular holes. The flow rate is based on the total opening area between the sleeve, holes, and spool, which extends or retracts according to the signal received at port S. Multiple Spool Orifice (IL) blocks can be connected for multiple sets of holes along a spool-sleeve pair.

If the spool displacement in your system is supplied by an external source or custom block and you would like the axial flow force to be transmitted to the system, you can use the Spool Orifice Flow Force (IL) block, which applies the same equations for force as the Spool Orifice (IL) block.

Flow Force

The force on the spool is calculated as:

$F = \frac{- {\dot{m}}_{A}^{2}}{ρ A} \cos (α) ε,$

where:

${\dot{m}}_{A}$ is the mass flow rate at port A.
ρ is the fluid density.
A is the orifice open area, which is determined by the spool position and orifice parameterization.
α is the jet angle, which is calculated from an approximation of the von Mises formula:

$α_{j e t} = 0.3663 + 0.8373 (1 - e^{\frac{- h}{1.848 c}}),$
where c is the Radial clearance, and h is the orifice opening.
ε is the Orifice orientation, which indicates orifice opening that is associated with a positive or negative signal at S.

Orifice Opening Area

For variable orifices, setting Orifice orientation to Positive spool displacement opens the orifice indicates that the orifice opens when the control member extends, while Negative spool displacement opens the orifice indicates that the orifice opens when the control member retracts.

The Leakage area, A_leak, is considered a small area open to flow when the orifice is closed, which maintains numerical continuity. Additionally, a nonzero Smoothing factor can provide increased numerical stability when the orifice is in near-closed or near-open position.

Round Holes

Setting Orifice parameterization to Round holes evenly distributes a user-defined number of holes along the sleeve perimeter with the equal diameters and centers aligned in the same plane.

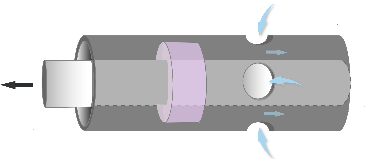
The open area expression is based on a geometric derivation and calculates the area of each hole as a planar circle. If the sleeve is cylindrical, the holes are not planar and this expression is an approximation. The open area is

$A_{o r i f i c e} = n_{0} \frac{d_{0}^{2}}{8} (θ - \sin (θ)) + A_{l e a k},$

where:

n₀ is the number of holes.
d₀ is the diameter of the holes.
A_leak is $A_{l e a k} = c d_{0} n_{0} .$
θ is the orifice opening area.

θ is set by the control signal at S

$θ = 2 \cos^{- 1} (1 - \frac{2 Δ S}{d_{0}}),$

where ΔS is the control member travel distance, ε(S - S_min), where S_min is the Control member position at closed orifice.

The maximum open area is:

$A_{\max} = \frac{π}{4} d_{0}^{2} n_{0} + A_{l e a k} .$

Rectangular Slot

Setting Orifice parameterization to Rectangular slot models one rectangular slot in the tube sleeve.

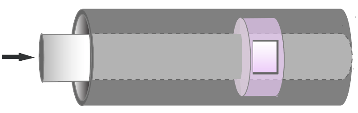
For an orifice with a slot in a rectangular sleeve, the open area is

$A_{o r i f i c e} = w Δ S + A_{l e a k},$

where w is the orifice width.

The maximum opening distance between the sleeve and case is:

$A_{\max} = w Δ S_{\max} + A_{l e a k} .$

where ΔS_max is the slot orifice Spool travel between closed and open orifice distance.

At the minimum orifice opening area, the leakage area is:

$A_{l e a k} = c w .$

Numerically-Smoothed Displacement

At the extremes of the orifice opening range, you can maintain numerical robustness in your simulation by adjusting the block Smoothing factor. The block applies a smoothing function to every calculated displacement, but primarily influences the simulation at the extremes of this range.

If the Smoothing factor parameter is nonzero, the block smoothly saturates the orifice opening between 0 and ΔS_max where ΔS_max is the:

Value of the Diameter of round holes parameter, when Orifice parameterization is set to Round holes.
Value of the Spool travel between closed and open orifice parameter, when Orifice parameterization is set to Rectangular slot.

For more information, see Numerical Smoothing.

The Mass Flow Rate Equation

The flow through a spool orifice is calculated by the pressure-flow rate equation:

$\dot{m} = \frac{C_{d} A_{o r i f i c e} \sqrt{2 \bar{ρ}}}{\sqrt{P R_{l o s s} (1 - {(\frac{A_{o r i f i c e}}{A})}^{2})}} \frac{Δ p}{{[Δ p^{2} + Δ p_{c r i t}^{2}]}^{1 / 4}},$

where:

C_d is the Discharge coefficient.
A is the Cross-sectional area at ports A and B.
$\bar{ρ}$ is the average fluid density.
A_orifice, is the orifice open area, unless:
- The opening is larger than or equal to the area at the Spool travel between closed and open orifice distance. The orifice area is then A_max.
- The orifice opening is less than or equal to the minimum opening distance. The orifice area is then A_leak.

The critical pressure difference, Δp_crit, is the pressure differential associated with the Critical Reynolds number, Re_crit, which is the point of transition between laminar and turbulent flow in the fluid:

$Δ p_{c r i t} = \frac{π \bar{ρ}}{8 A_{o r i f i c e}} {(\frac{ν {Re}_{c r i t}}{C_{d}})}^{2} .$

Pressure loss describes the reduction of pressure in the orifice due to a decrease in area. PR_loss is calculated as:

$P R_{l o s s} = \frac{\sqrt{1 - {(\frac{A_{o r i f i c e}}{A_{p o r t}})}^{2} (1 - C_{d}^{2})} - C_{d} \frac{A_{o r i f i c e}}{A_{p o r t}}}{\sqrt{1 - {(\frac{A_{o r i f i c e}}{A_{p o r t}})}^{2} (1 - C_{d}^{2})} + C_{d} \frac{A_{o r i f i c e}}{A_{p o r t}}} .$

Pressure recovery describes the positive pressure change in the orifice due to an increase in area. If you do not wish to capture this increase in pressure, clear the Pressure recovery check box. In this case, PR_loss is 1.

Assumptions and Limitations

The transient effects are negligible.
The jet angle approximation is based on the Richard von Mises equation.
The jet angle variation with the orifice opening is identical for the rectangular slot and the round holes orifices.

Examples

Diesel Engine In-Line Injection System

An in-line multi-element diesel injection system. It consists of a cam shaft, a lift pump, four in-line injection pumps, and four injectors.

Open Model

Hydraulic Axial-Piston Pump with Load-Sensing and Pressure-Limiting Control

A test rig designed to investigate the interaction between an axial-piston pump and a typical control unit simultaneously performing the load-sensing and pressure-limiting functions. To increase the fidelity of the simulation, this example uses a detailed model of the pump that accounts for the interaction between the pistons, swash plate, and valve plate.

Open Model

Ports

Conserving

expand all

A — Liquid port
isothermal liquid

Entry or exit port of the liquid to or from the orifice.

B — Liquid port
isothermal liquid

Entry or exit port of the liquid to or from the orifice.

Input

expand all

S — Control member displacement, m
physical signal

Control member displacement for a variable-area orifice, in m.

Output

expand all

F — Flow force, N
physical signal

Axial flow force, in N.

Parameters

expand all

Orifice parameterization — Type of orifice
`Round holes` (default) | `Rectangular slot`

Hole geometry in the sleeve. The round holes are spaced evenly about the cross-sectional circumference. There is only one hole in the Rectangular slot setting.

Diameter of round holes — Diameter of round holes
`5e-3 m` (default) | positive scalar

Diameter of all holes on the sleeve.

Dependencies

To enable this parameter, set Orifice parametrization to Round holes.

Number of round holes — Number of round holes
`6` (default) | positive integer

Number of holes along the sleeve circumference.

Dependencies

To enable this parameter, set Orifice parametrization to Round holes.

Orifice width — Rectangular slot width
`0.01 m` (default) | positive scalar

Rectangular slot width.

Dependencies

To enable this parameter, set Orifice parametrization to Rectangular slot.

Spool travel between closed and open orifice — Control member maximum stroke
`5e-3 m` (default) | positive scalar

Maximum distance of the control member travel. This value provides an upper limit to calculations so that simulations do not return unphysical values.

Dependencies

To enable this parameter, set Orifice parametrization to Rectangular slot.

Flow force output — Whether to model axial hydraulic force on the spool
`off` (default) | `on`

Whether to model the axial hydraulic force on the spool. When you select this parameter, port F is enabled and outputs the axial force as a physical signal, in N.

Radial clearance — Spool-sleeve clearance
`1e-5 m` (default) | positive scalar

Radial distance between the spool and the sleeve.

Dependencies

To enable this parameter, select Flow force output.

Leakage area — Gap area when valve is in fully closed position
`1e-10` m^2 (default) | positive scalar

Sum of all gaps when the valve is in the fully closed position. Any area smaller than this value is saturated to the specified leakage area. This contributes to numerical stability by maintaining continuity in the flow.

Spool position at closed orifice — Spool offset
`0` (default) | scalar

Spool offset when the orifice is fully open. A positive, nonzero value indicates a partially closed orifice. A negative, nonzero value indicates an overlapped orifice that remains open for an initial displacement set by the physical signal at port S.

Cross-sectional area at ports A and B — Orifice area at conserving ports
`inf m^2` (default) | positive scalar

Cross-sectional area at the entry and exit ports A and B. This area is used in the pressure-flow rate equation that determines the mass flow rate through the orifice.

Opening orientation — Direction of changing orifice area
`Positive spool displacement opens the orifice` (default) | `Negative spool displacement opens the orifice`

Direction of the area change for variable orifices. A positive opening orientation indicates an increase in the orifice opening. A negative orientation indicates a decrease in the orifice opening. The magnitude is always positive.

Discharge coefficient — Discharge coefficient
`0.64` (default) | positive scalar in the range of [0,1]

Correction factor that accounts for discharge losses in theoretical flows.

Critical Reynolds number — Upper Reynolds number limit for laminar flow
`150` (default) | positive scalar

Upper Reynolds number limit for laminar flow through the orifice.

Smoothing factor — Numerical smoothing factor
`0.01` (default) | positive scalar

Continuous smoothing factor that introduces a layer of gradual change to the flow response when the orifice is in near-open or near-closed positions. Set this value to a nonzero value less than one to increase the stability of your simulation in these regimes.

Pressure recovery — Whether to account for pressure increase in area expansions
`off` (default) | `on`

Whether to account for pressure increase when fluid flows from a region of smaller cross-sectional area to a region of larger cross-sectional area.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

Introduced in R2020a

Spool Orifice (IL)

Description

Flow Force

Orifice Opening Area

Numerically-Smoothed Displacement

The Mass Flow Rate Equation

Assumptions and Limitations

Examples

Diesel Engine In-Line Injection System

Hydraulic Axial-Piston Pump with Load-Sensing and Pressure-Limiting Control

Ports

Conserving

A — Liquid port isothermal liquid

B — Liquid port isothermal liquid

Input

S — Control member displacement, m physical signal

Output

F — Flow force, N physical signal

Parameters

Orifice parameterization — Type of orifice Round holes (default) | Rectangular slot

Diameter of round holes — Diameter of round holes 5e-3 m (default) | positive scalar

Dependencies

Number of round holes — Number of round holes 6 (default) | positive integer

Dependencies

Orifice width — Rectangular slot width 0.01 m (default) | positive scalar

Dependencies

Spool travel between closed and open orifice — Control member maximum stroke 5e-3 m (default) | positive scalar

Dependencies

Flow force output — Whether to model axial hydraulic force on the spool off (default) | on

Radial clearance — Spool-sleeve clearance 1e-5 m (default) | positive scalar

Dependencies

Leakage area — Gap area when valve is in fully closed position 1e-10 m^2 (default) | positive scalar

Spool position at closed orifice — Spool offset 0 (default) | scalar

Cross-sectional area at ports A and B — Orifice area at conserving ports inf m^2 (default) | positive scalar

Opening orientation — Direction of changing orifice area Positive spool displacement opens the orifice (default) | Negative spool displacement opens the orifice

Discharge coefficient — Discharge coefficient 0.64 (default) | positive scalar in the range of [0,1]

Critical Reynolds number — Upper Reynolds number limit for laminar flow 150 (default) | positive scalar

Smoothing factor — Numerical smoothing factor 0.01 (default) | positive scalar

Pressure recovery — Whether to account for pressure increase in area expansions off (default) | on

Extended Capabilities

C/C++ Code Generation Generate C and C++ code using Simulink® Coder™.

Version History

See Also

A — Liquid port
isothermal liquid

B — Liquid port
isothermal liquid

S — Control member displacement, m
physical signal

F — Flow force, N
physical signal

Orifice parameterization — Type of orifice
`Round holes` (default) | `Rectangular slot`

Diameter of round holes — Diameter of round holes
`5e-3 m` (default) | positive scalar

Number of round holes — Number of round holes
`6` (default) | positive integer

Orifice width — Rectangular slot width
`0.01 m` (default) | positive scalar

Spool travel between closed and open orifice — Control member maximum stroke
`5e-3 m` (default) | positive scalar

Flow force output — Whether to model axial hydraulic force on the spool
`off` (default) | `on`

Radial clearance — Spool-sleeve clearance
`1e-5 m` (default) | positive scalar

Leakage area — Gap area when valve is in fully closed position
`1e-10` m^2 (default) | positive scalar

Spool position at closed orifice — Spool offset
`0` (default) | scalar

Cross-sectional area at ports A and B — Orifice area at conserving ports
`inf m^2` (default) | positive scalar

Opening orientation — Direction of changing orifice area
`Positive spool displacement opens the orifice` (default) | `Negative spool displacement opens the orifice`

Discharge coefficient — Discharge coefficient
`0.64` (default) | positive scalar in the range of [0,1]

Critical Reynolds number — Upper Reynolds number limit for laminar flow
`150` (default) | positive scalar

Smoothing factor — Numerical smoothing factor
`0.01` (default) | positive scalar

Pressure recovery — Whether to account for pressure increase in area expansions
`off` (default) | `on`

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.