非线性灰盒模型

估计非线性微分方程、差分方程和状态空间方程的系数

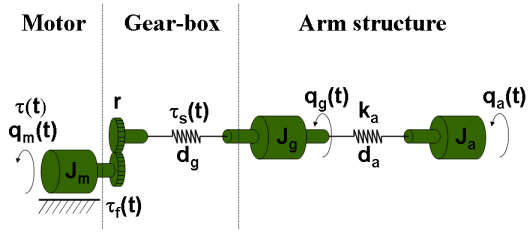
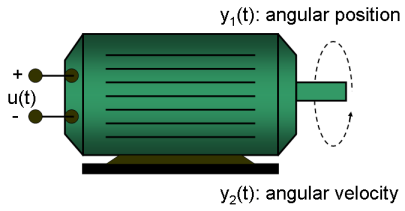
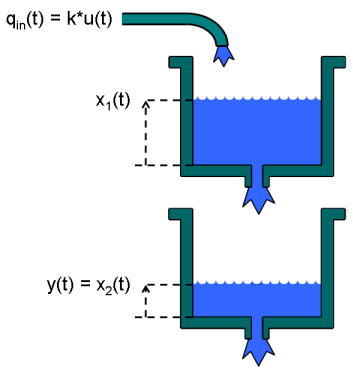
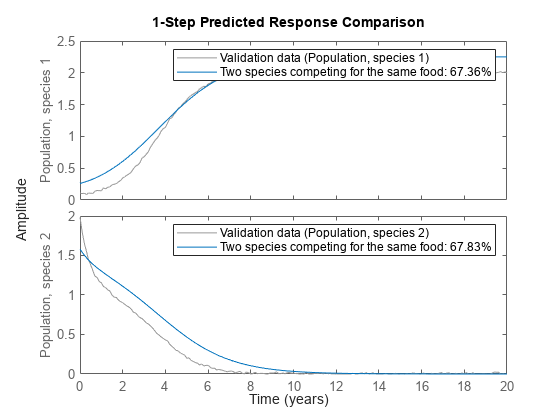
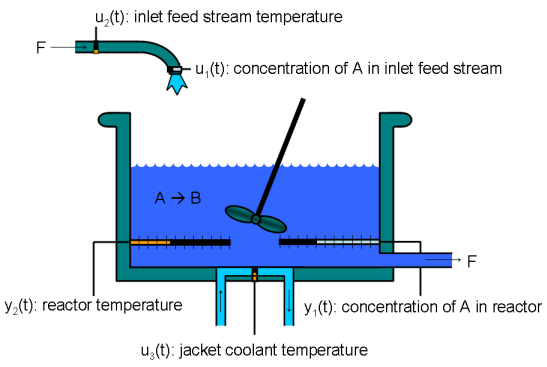
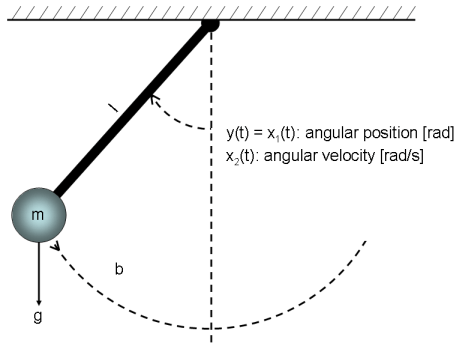
如果您了解系统的物理特性，并且可以使用具有未知参数的常微分方程或差分方程 (ODE) 来表示系统，则可以使用 System Identification Toolbox™ 命令执行灰盒建模。灰盒模型 ODE 明确指定模型的数学结构，包括参数之间的耦合。当您了解变量之间的关系、模型行为的约束或表示系统动态特性的显式方程时，灰盒建模是很有用的。

您可以使用 idnlgrey 对象表示非线性灰盒模型，这需要您编写一个函数将动态特性描述为一组一阶微分方程。有关详细信息，请参阅Estimate Nonlinear Grey-Box Models。

函数

全部展开

模型估计

`nlgreyest`	Estimate nonlinear grey-box model parameters
`nlgreyestOptions`	Option set for `nlgreyest`
`idnlgrey`	Nonlinear grey-box model
`pem`	Prediction error minimization for refining linear and nonlinear models
`generateMATLABFunction`	Generate MATLAB functions that evaluate the state and output functions, and their Jacobians, of a nonlinear grey-box or neural state-space model (自 R2022b 起)

模型参数

`init`	Set or randomize initial parameter values
`getpar`	Parameter values and properties of `idnlgrey` model parameters
`setpar`	Set initial parameter values of `idnlgrey` model object
`getpvec`	Obtain model parameters and associated uncertainty data
`setpvec`	Modify values of model parameters

模型状态

`getinit`	Values of `idnlgrey` model initial states
`setinit`	设置 `idnlgrey` 模型对象的初始状态
`findstates`	Estimate initial states of model
`findstatesOptions`	Option set for `findstates`

仿真

`sim`	Simulate response of identified model
`simOptions`	Option set for `sim`

主题

Linear and Nonlinear Grey-Box Modeling
If you understand the physics of your system, you can estimate linear or nonlinear grey-box models.
Estimate Nonlinear Grey-Box Models
How to define and estimate nonlinear grey-box models at the command line.
Creating IDNLGREY Model Files
This example shows how to write ODE files for nonlinear grey-box models as MATLAB® and C MEX files.
Estimate Coefficients of ODEs to Fit Given Solution
Estimate model parameters using linear and nonlinear grey-box modeling.