pem

预测误差最小化用于优化线性与非线性模型

全页折叠

语法

sys = pem(data,init_sys)

sys = pem(data,init_sys,opt)

说明

sys = pem(data,init_sys) 更新初始模型 init_sys 的参数以拟合 data 中的估计数据。data 可以是时间表、以逗号分隔的矩阵对，或数据对象。

该函数采用预测误差最小化算法来更新初始模型的参数。使用此命令来优化先前估计模型的参数。

示例

sys = pem(data,init_sys,opt) 使用选项集指定估计选项。

示例

全部折叠

优化估计的状态空间模型

打开实时脚本

使用 n4sid 进行离散时间状态空间建模，该方法采用子空间法。

加载数据并提取前 300 个点作为估计数据。

load sdata7 tt7;
tt7e = tt7(1:300,:);

估计模型 init_sys，将 'Focus' 选项设置为 'simulation'。

opt = n4sidOptions('Focus','simulation');
init_sys = n4sid(tt7e,4,opt);

显示估计拟合。

init_sys.Report.Fit.FitPercent

ans = 
73.8490

使用 pem 来提高贴合度。

sys = pem(tt7e,init_sys);

分析得到的结果。

compare(tt7e,sys,init_sys);

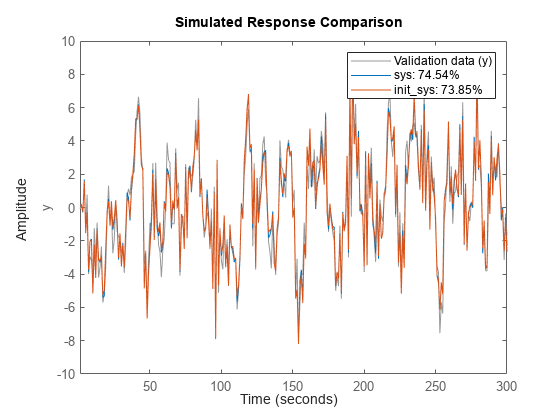
$Figure contains an axes object. The axes object with ylabel y contains 3 objects of type line. These objects represent Validation data (y), sys: 74.54%, init\_sys: 73.85%.$

使用 pem 可改善对估计数据的拟合效果。

估计非线性灰盒模型

打开实时脚本

估计非线性灰箱模型的参数以拟合直流电机数据。

加载实验数据，并指定信号属性，例如起始时间和单位。

load('dcmotordata');
data = iddata(y, u, 0.1);
data.Tstart = 0;
data.TimeUnit = 's';

配置非线性灰箱模型 (idnlgrey)。

在本示例中，请使用 dcmotor_m.m 文件。要在 MATLAB® 命令提示符下查看此文件，请输入 edit dcmotor_m.m。

file_name = 'dcmotor_m';
order = [2 1 2];
parameters = [1;0.28];
initial_states = [0;0];
Ts = 0;
init_sys = idnlgrey(file_name,order,parameters,initial_states,Ts);
init_sys.TimeUnit = 's';

setinit(init_sys,'Fixed',{false false});

init_sys 是一个非线性灰盒模型，其结构由 dcmotor_m.m 描述。该模型具有一个输入、两个输出和两个状态，具体由 order 定义。

setinit(init_sys,'Fixed',{false false}) 指定 init_sys 的初始状态为自由估计参数。

估计模型参数和初始状态。

sys = pem(data,init_sys);

sys 是 idnlgrey 模型，该模型封装了估计参数及其协方差。

分析估计结果。

compare(data,sys,init_sys);

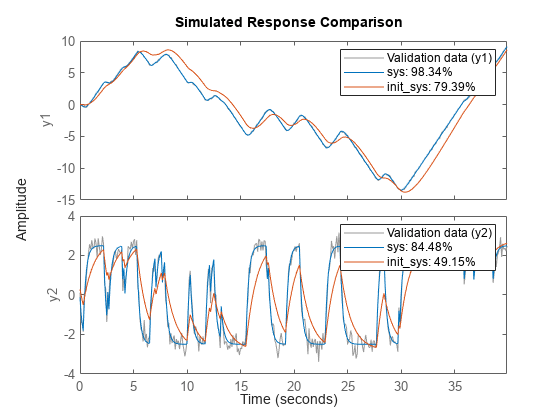
$Figure contains 2 axes objects. Axes object 1 with ylabel y1 contains 3 objects of type line. These objects represent Validation data (y1), sys: 98.34%, init\_sys: 79.39%. Axes object 2 with ylabel y2 contains 3 objects of type line. These objects represent Validation data (y2), sys: 84.48%, init\_sys: 49.15%.$

sys 模型对估计数据的拟合度为 98.34%。

使用流程模型配置估计

打开实时脚本

创建流程模型结构并更新其参数值，以最小化预测误差。

初始化过程模型的系数。

init_sys = idproc('P2UDZ');
init_sys.Kp = 10;
init_sys.Tw = 0.4;
init_sys.Zeta = 0.5;
init_sys.Td = 0.25;
init_sys.Tz = 0.01;

init_sys 的 Kp、Tw、Zeta、Td 和 Tz 系数均配置了其初始猜测值。

使用 init_sys 配置基于测量数据的预测误差最小化模型估计。由于 init_sys 是 idproc 模型，请使用 procestOptions 创建选项集。

load iddata1 z1;
opt = procestOptions('Display','on','SearchMethod','lm');
sys = pem(z1,init_sys,opt);

Process Model Identification
                            
Estimation data: Time domain data z1         
Data has 1 outputs, 1 inputs and 300 samples.
Model Type:   
    {'P2DUZ'}


Algorithm: Levenberg-Marquardt search
 <br>
------------------------------------------------------------------------------------------
 <br>
                          Norm of      First-order    Improvement (%) <br> Iteration       Cost       step         optimality     Expected   Achieved    Bisections <br>------------------------------------------------------------------------------------------
     0        29.7194          -            260        2.57           -         -                                                                                                                                                                                                                                                                                                                               
     1        28.6801          6           98.9        2.57         3.5         0
     2        8.38196       4.91           42.2        2.72        70.8         0
     3         8.2138      0.704           41.3        1.37        2.01        12
     4        8.00237      0.528           48.3        2.89        2.57         9
     5        7.65577      0.588           73.1        2.02        4.33         9
     6          6.851      0.809            196        4.51        10.5         9
     7        5.72335       1.08            459        4.59        16.5         8
     8         3.3434       2.11       1.63e+03        11.4        41.6         7
     9        1.80724      0.701            504        14.2        45.9         0
    10         1.6812      0.122             12        4.24        6.97         0
    11        1.68092      0.014           1.11       0.309      0.0168         0
    12        1.68092    0.00179         0.0215         0.3    0.000101         0
    13        1.68092   0.000112        0.00634         0.3    8.26e-07         0
    14        1.68092   1.36e-05       0.000382         0.3    7.62e-09         0
    15        1.68092   1.18e-06       5.01e-05         0.3    7.28e-11         0
    16        1.68092   1.23e-07       4.29e-06         0.3    7.13e-13         0
    17        1.68092   1.17e-08       4.56e-07         0.3    1.32e-14         0
------------------------------------------------------------------------------------------
Termination condition: No improvement along the search direction with line search..
Number of iterations: 18, Number of function evaluations: 115                      
                                                                                   
Status: Estimated using PEM                                                        
Fit to estimation data: 70.57%, FPE: 1.7379

检查模型拟合度。

sys.Report.Fit.FitPercent

ans = 
       70.567

sys 模型对测量数据的拟合度为 70.63%。

输入参数

全部折叠

`data` — 估计数据
时间表 | 矩阵 | `iddata object` | `idfrd` 对象 | `frd` 对象 | 时间表的元胞数组 | 矩阵对的元胞数组

均匀采样估计数据，可指定为时间表、逗号分隔的矩阵对或数据对象，具体如下文所述。对于多实验数据，data 也可以是一个 1×N_e 的元胞数组，其中包含时间表或矩阵对，其中 N_e 是实验的数量。数据对象可在对象内部容纳多实验数据。

时间表

将 data 指定为使用等间隔时间向量的 timetable。tt 包含表示输入和输出通道的变量。pem 从作为输入参量传递的模型中推导出输入和输出通道变量。

以逗号分隔的矩阵对

将 data 指定为由实数矩阵组成的以逗号分隔的成对数据，其中包含输入和输出时域信号值。

对于单输入单输出系统，请将 data 指定为一对 N_s×1 实数矩阵，其中包含均匀采样的输入和输出时域信号值。这里，N_s 是采样数。
对于 MIMO 系统，指定 u,y 作为具有以下维度的输入/输出矩阵对：
- u - N_sxN_u，其中 N_u 是输入数目。
- y - N_sxN_y，其中 N_y 是输出数目。

数据对象

将数据指定为 iddata、idfrd 或 frd 对象。

如果作为输入参量传递的模型是：

参数化模型例如 idss，然后 data 可以是 iddata，idfrd 或 frd 模型对象。
频率响应数据模型（idfrd 或 frd 模型对象），则 data 也必须是频率响应数据模型。
如果是 iddata 对象，则 data 必须是一个具有匹配域、试验的数量和时间或频率向量的 iddata 对象。

有关使用估计数据类型的详细信息，请参阅Data Domains and Data Types in System Identification Toolbox。

`init_sys` — 已识别出配置 `sys` 初始参数化的模型
线性模型 | 非线性模型

用于配置 sys 初始参数化的标识模型，指定为线性或非线性模型。您可以通过使用测量数据进行估计或直接构造来获得 init_sys。

init_sys 必须具有有限的参数值。您可以配置初始猜测值，指定最小/最大边界，并为 init_sys 的任何参数估计设置固定或自由参数：

对于线性模型，请使用 Structure 属性。有关详细信息，请参阅Imposing Constraints on Model Parameter Values。
对于非线性灰箱模型，请使用 InitialStates 和 Parameters 属性。对于非线性 ARX 模型和 Hammerstein-Wiener 模型，无法指定参数约束。

`opt` — 估计选项
选项集

估计选项，用于配置算法设置、处理估计焦点、初始条件和数据偏移量，以选项集的形式指定。创建选项集所使用的命令取决于初始模型类型：

模型类型	使用
`idss`	`ssestOptions`
`idtf`	`tfestOptions`
`idproc`	`procestOptions`
`idpoly`	`polyestOptions`
`idgrey`	`greyestOptions`
`idnlarx`	`nlarxOptions`
`idnlhw`	`nlhwOptions`
`idnlgrey`	`nlgreyestOptions`

输出参量

全部折叠

`sys` — 辨识模型
线性模型 | 非线性模型

已识别模型，返回与 init_sys 相同的模型类型。该模型是通过预测误差最小化算法估计 init_sys 的自由参数而获得的。

算法

PEM 采用数值优化方法来最小化预测误差的加权范数 cost function，对于标量输出，其定义如下：

$V_{N} (G, H) = \sum_{t = 1}^{N} e^{2} (t)$

其中 e(t) 是模型测量输出与预测输出之间的差值。对于线性模型，误差定义为：

$e (t) = H^{- 1} (q) [y (t) - G (q) u (t)]$

其中 e(t) 是向量，而成本函数 $V_{N} (G, H)$ 是标量值。下标 N 表明成本函数是数据样本数量的函数，且随着 N 值增大而变得更精确。对于多输出模型，上述方程更为复杂。更多信息请参阅第 7 章系统辨识：用户理论，第二版，作者：伦纳特·吕恩，普伦蒂斯厅出版社，1999 年。

替代功能

通过使用针对不同模型结构的专用估计命令，您可获得与 pem 相同的估计结果。例如，使用 ssest(data,init_sys) 进行状态空间模型的估计。

版本历史记录

在 R2006a 之前推出

另请参阅

主题

Refine Linear Parametric Models

pem

语法

说明

示例

优化估计的状态空间模型

估计非线性灰盒模型

使用流程模型配置估计

输入参数

data — 估计数据 时间表 | 矩阵 | iddata object | idfrd 对象 | frd 对象 | 时间表的元胞数组 | 矩阵对的元胞数组

时间表

以逗号分隔的矩阵对

数据对象

init_sys — 已识别出配置 sys 初始参数化的模型 线性模型 | 非线性模型

opt — 估计选项 选项集

输出参量

sys — 辨识模型 线性模型 | 非线性模型

算法

替代功能

版本历史记录

另请参阅

主题

`data` — 估计数据
时间表 | 矩阵 | `iddata object` | `idfrd` 对象 | `frd` 对象 | 时间表的元胞数组 | 矩阵对的元胞数组

`init_sys` — 已识别出配置 `sys` 初始参数化的模型
线性模型 | 非线性模型

`opt` — 估计选项
选项集

`sys` — 辨识模型
线性模型 | 非线性模型