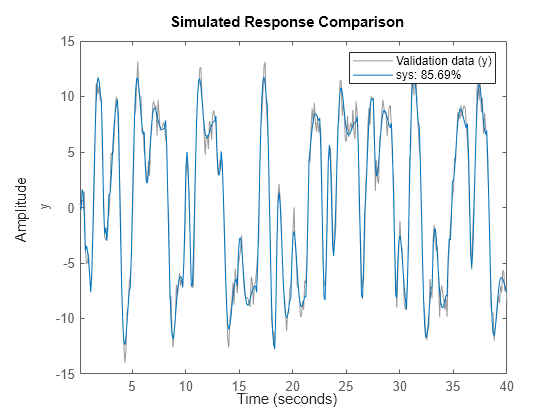
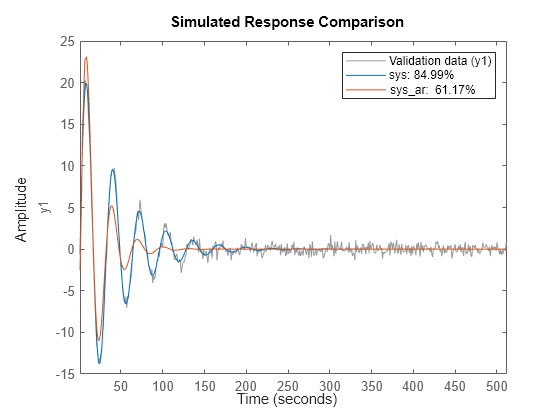
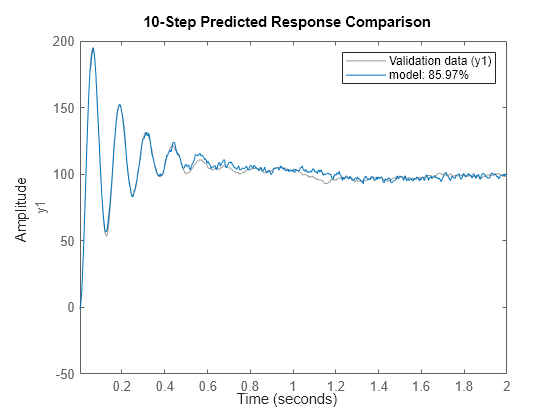
armax

使用时域数据估计 ARMAX、ARIMAX、ARMA 或 ARIMA 模型的参数

全页折叠

语法

sys = armax(tt,[na nb nc nk])

sys = armax(u,y,[na nb nc nk])

sys = armax(data,[na nb nc nk])

sys = armax(___,Name,Value)

sys = armax(tt,init_sys)

sys = armax(u,y,init_sys)

sys = armax(data,init_sys)

sys = armax(___,opt)

[sys,ic] = armax(___)

说明

估计 ARMAX 或 ARMA 模型

sys = armax(tt,[na nb nc nk]) 使用时间表 tt 的变量中包含的数据来估计 ARMAX 或 ARMA idpoly 模型 sys 的参数。软件以第一个 Nu 个变量作为输入，以接下来的 Ny 个变量作为输出，其中 Nu 和 Ny 分别由 nb 和 na 的维度确定。

对于没有输入信号的 ARMA 模型，使用 sys = armax(tt,na)。在这种情况下，软件使用第一个 Ny 变量来拟合模型。

armax 使用预测误差方法和 [na nb nc nk] 中指定的多项式阶数执行估计。模型属性包括估计协方差（参数不确定性）以及估计数据和测量数据之间的拟合优度。

要从 tt 中选择特定的输入和输出通道，请使用名称-值语法将 'InputName' 和 'OutputName' 设置为相应的时间表变量名称。

示例

sys = armax(u,y,[na nb nc nk]) 使用逗号分隔的矩阵 u,y 中的时域输入和输出信号。软件假设数据采样时间为 1 秒。要更改采样时间，请使用名称-值语法设置 Ts。

sys = armax(data,[na nb nc nk]) 使用 iddata 对象 data 中的时域数据。特别是当您想利用数据对象提供的附加信息（例如数据采样时间或试验标注）时，请使用此语法。

示例

sys = armax(___,Name,Value) 使用一个或多个名称-值参量指定附加选项。例如，使用名称-值参量 'IntegrateNoise',1 估计 ARIMAX 或 ARIMA 模型，这对于具有非平稳扰动的系统很有用。在任意先前的输入参数组合之后指定 Name,Value。

示例

配置初始参数

sys = armax(tt,init_sys) 使用离散时间线性系统 init_sys 配置 sys 的初始参数化，以便使用时间表 tt 进行估计。

示例

sys = armax(u,y,init_sys)使用矩阵数据 u,y 进行估计。

sys = armax(data,init_sys) 使用数据对象 data 进行估计。

指定其他估计选项

sys = armax(___,opt) 包含一个选项集 opt，该选项集指定了用于估计的初始条件处理、正则化和数值搜索方法等选项。

示例

返回估计的初始条件

[sys,ic] = armax(___) 将估计的初始条件作为 initialCondition 对象返回。如果您计划使用相同的估计输入数目据来仿真或预测模型响应，然后将响应与相同的估计输出数目据进行比较，请使用此语法。结合初始条件，在仿真的第一部分可以得到更好的匹配。

示例

全部折叠

估计 ARMAX 模型

打开实时脚本

估计 ARMAX 模型并查看模型输出与估计数据的拟合程度。

在时间表 tt2 中加载测量数据。

load sdata2 tt2

估计具有二阶 $A$ 、 $B$ 和 $C$ 多项式以及一个采样周期的传输延迟的 ARMAX 模型。

na = 2;
nb = 2;
nc = 2;
nk = 1;
sys = armax(tt2,[na nb nc nk])

sys =
Discrete-time ARMAX model: A(z)y(t) = B(z)u(t) + C(z)e(t)
  A(z) = 1 - 1.512 z^-1 + 0.7006 z^-2                    
                                                         
  B(z) = -0.2606 z^-1 + 1.664 z^-2                       
                                                         
  C(z) = 1 - 1.604 z^-1 + 0.7504 z^-2                    
                                                         
Sample time: 0.1 seconds
  
Parameterization:
   Polynomial orders:   na=2   nb=2   nc=2   nk=1
   Number of free coefficients: 6
   Use "polydata", "getpvec", "getcov" for parameters and their uncertainties.

Status:                                          
Estimated using ARMAX on time domain data "tt2". 
Fit to estimation data: 85.89% (prediction focus)
FPE: 1.086, MSE: 1.054                           
 
Model Properties

输出显示包含估计参数的多项式以及估计细节。在 Status, Fit to estimation data 下显示估计模型的 1 步预测准确率在 80% 以上。

将模型仿真输出与测量数据进行比较。

compare(tt2,sys)

Figure contains an axes object. The axes object with ylabel y contains 2 objects of type line. These objects represent Validation data (y), sys: 85.69%.

仿真模型与测量数据的拟合度与估计拟合度几乎相同。

ARMA 模型

打开实时脚本

估计 ARMA 模型并将其响应与测量输出和 AR 模型进行比较。

加载数据，其中包含带有噪声的时间序列 ymat9。

load sdata9 ymat9

用一阶 $C$ 多项式估计四阶 ARMA 模型。

na = 4;
nc = 1;
sys = armax(ymat9,[na nc]);

估计四阶 AR 模型。

sys_ar = ar(ymat9,na);

将模型输出与测量数据进行比较。

compare(ymat9,sys,sys_ar)

$Figure contains an axes object. The axes object with ylabel y1 contains 3 objects of type line. These objects represent Validation data (y1), sys: 84.99%, sys\_ar: 61.17%.$

ARMA 模型对数据的拟合效果较好。

指定估计选项

打开实时脚本

从测量数据估计 ARMAX 模型并指定估计选项。

加载数据并创建一个 iddata 对象。初始化选项集 opt，并设置 Focus、SearchMethod、MaxIterations 和 Display 的选项。然后使用更新后的选项集估计 ARMAX 模型。

load twotankdata;
z = iddata(y,u,0.2);
opt = armaxOptions;
opt.Focus = 'simulation';
opt.SearchMethod = 'lm';
opt.SearchOptions.MaxIterations = 10;
opt.Display = 'on';
sys = armax(z,[2 2 2 1],opt);

进度查看器中显示的模型测量组件的终止条件是达到最大迭代次数。

为了改善结果，请使用更大的 MaxIterations 值重新估计模型，或者继续对之前估计的模型进行如下迭代：

sys2 = armax(z,sys);
compare(z,sys,sys2)

其中 sys2 细化了 sys 的参数以改善数据拟合。

具有正则化的 ARMAX 模型

打开实时脚本

通过转换正则化的 ARX 模型来估计正则化的 ARMAX 模型。

加载数据。

load regularizationExampleData.mat m0simdata;

估计阶数为 30 的非正则化 ARMAX 模型。

m1 = armax(m0simdata(1:150),[30 30 30 1]);

通过反复试验确定 Lambda 值来估计正则化 ARMAX 模型。

opt = armaxOptions;
opt.Regularization.Lambda = 1;
m2 = armax(m0simdata(1:150),[30 30 30 1],opt);

通过转换正则化的 ARX 模型，然后进行降阶，得到低阶的 ARMAX 模型。

opt1 = arxOptions;
[L,R] = arxRegul(m0simdata(1:150),[30 30 1]);
opt1.Regularization.Lambda = L;
opt1.Regularization.R = R;
m0 = arx(m0simdata(1:150),[30 30 1],opt1);
mr = idpoly(balred(idss(m0),7));

将模型输出与数据进行比较。

opt2 = compareOptions('InitialCondition','z');
compare(m0simdata(150:end),m1,m2,mr,opt2);

Figure contains an axes object. The axes object with ylabel y1 contains 4 objects of type line. These objects represent Validation data (y1), m1: 41.22%, m2: 52.13%, mr: 64.91%.

ARIMA 模型

打开实时脚本

估计单变量时间序列数据的四阶 ARIMA 模型。

加载包含噪声的时间序列的数据。

load iddata9 z9;

对输出信号进行积分，并使用结果替换 z9 中的原始输出信号。

z9.y = cumsum(z9.y);

通过将 'IntegrateNoise' 设置为 true，用一阶 $C$ 多项式估计四阶 ARIMA 模型。

model = armax(z9,[4 1],'IntegrateNoise',true);

使用 10 步预测来预测模型输出，并将预测输出与估计数据进行比较。

compare(z9,model,10)

Figure contains an axes object. The axes object with ylabel y1 contains 2 objects of type line. These objects represent Validation data (y1), model: 85.97%.

迭代估计 ARMAX 模型

打开实时脚本

根据测量数据迭代估计不同阶数的 ARMAX 模型。

加载 dryer2 数据并对多项式阶数 na、nb、nc 和输入延迟 nk 的组合进行估计。

load dryer2;
z = iddata(y2,u2,0.08,'Tstart',0);
na = 2:4;
nc = 1:2;
nk = 0:2;
models = cell(1,18);
ct = 1;
for i = 1:3
    na_ = na(i);
    nb_ = na_;
    for j = 1:2
        nc_ = nc(j);
        for k = 1:3
            nk_ = nk(k); 
            models{ct} = armax(z,[na_ nb_ nc_ nk_]);
            ct = ct+1;
        end
    end
end

堆叠估计模型并将它们的仿真响应与估计数据 z 进行比较。

models = stack(1,models{:});
compare(z,models)

使用状态空间模型初始化 ARMAX 模型参数

打开实时脚本

加载估计数据。

load sdata2 umat2 ymat2

从估计数据中估计 3 阶状态空间模型。

sys0 = n4sid(umat2,ymat2,3);

使用先前估计的状态空间模型来估计 ARMAX 模型以初始化参数。

sys = armax(umat2,ymat2,sys0);
compare(umat2,ymat2,sys)

Figure contains an axes object. The axes object with ylabel y1 contains 2 objects of type line. These objects represent Validation data (y1), sys: 86.56%.

获取初始条件

打开实时脚本

加载数据。

load iddata1ic z1i

估计二阶 ARMAX 模型 sys 并返回 ic 中的初始条件。

na = 2;
nb = 2;
nc = 2;
nk = 1;
[sys,ic] = armax(z1i,[na nb nc nk]);
ic

ic = 
  initialCondition with properties:

     A: [2×2 double]
    X0: [2×1 double]
     C: [0 1]
    Ts: 0.1000

ic 是一个 initialCondition 对象，它以状态空间形式封装了 sys 对 X0 中的初始状态向量的自由响应。当您使用 z1i 输入信号仿真 sys 并将响应与 z1i 输出信号进行比较时，您可以合并 ic。

输入参数

全部折叠

`tt` — 基于时间表的估计数据
时间表 | 时间表的元胞数组。

估计数据，指定为使用固定间隔时间向量的 timetable。tt 包含表示输入和输出通道的变量。对于多试验数据，tt 是长度为 Ne 的时间表元胞数组，其中 Ne 是试验的数量。

软件根据指定多项式阶数的维度确定用于估计的输入和输出通道的数量。输入/输出通道选择取决于是否指定了 'InputName' 和 'OutputName' 名称-值参量。

如果未指定 'InputName' 和 'OutputName'，则软件将使用 tt 的第一个 Nu 变量作为输入，使用 tt 的下一个 Ny 变量作为输出。
如果指定了 'InputName' 和 'OutputName'，则软件使用指定的变量。指定的输入和输出名称的数量必须与 Nu 和 Ny 一致。
对于可以估计时间序列模型的函数，如果没有输入，则不需要指定 'InputName'。

有关使用估计数据类型的详细信息，请参阅Data Domains and Data Types in System Identification Toolbox。

`u`, `y` — 基于矩阵的估计数据
矩阵 | 由矩阵组成的元胞数组

估计数据，对于 SISO 系统指定为以逗号分隔的 N_s×1 实值矩阵对，其中包含均匀采样的输入和输出时域信号值。这里，N_s 是采样数。

对于 MIMO 系统，指定 u,y 作为具有以下维度的输入/输出矩阵对：

u - N_sxN_u，其中 N_u 是输入数目。
y - N_sxN_y，其中 N_y 是输出数目。

对于多试验数据，将 u、y 指定为一对 1×N_e 元胞数组数组，其中 N_e 是试验的数量。所有试验的采样时间必须匹配。

对于仅包含输出而不包含输入的时间序列数据，请指定 [],y。

有关使用估计数据类型的详细信息，请参阅Data Domains and Data Types in System Identification Toolbox。

`data` — 时域估计数据
`iddata` 对象

时域估计数据，指定为 iddata 对象。对于 ARMA 和 ARIMA 时间序列模型，data 中的输入通道必须为空。例如，请参阅ARMA 模型和ARIMA 模型。

`[na nb nc nk]` — 多项式阶数
整数行向量 | 整数矩阵的行向量 | 标量

模型的多项式阶数和延迟，指定为 1×4 向量或矩阵向量 [na nb nc nk]。多项式的阶等于该多项式中要估计的系数的数量。

对于没有输入的 ARMA 或 ARIMA 时间序列模型，将 [na nb nc nk] 设置为 [na nc]。有关示例，请参阅ARMA 模型。

对于具有 Ny 输出和 Nu 输入的模型：

na 是多项式 A(q) 的阶，指定为非负整数的 Ny×Ny 矩阵。
nb 是多项式 B(q) + 1 的阶，指定为非负整数的 Ny×Nu 矩阵。
nc 是多项式 C(q) 的阶，指定为长度为 Ny 的非负整数列向量。
nk 是输入-输出延迟，也称为传输延迟，指定为非负整数的 Ny×Nu 矩阵。nk 在 ARMAX 模型中由 B 多项式的固定前导零表示。

有关示例，请参阅估计 ARMAX 模型。

`init_sys` — 用于配置初始参数化的系统
离散时间线性模型

用于配置 sys 的初始参数化的系统，指定为离散时间线性模型。您可以通过使用测量数据进行估计或使用 idpoly 和 idss 等命令直接构造来获得 init_sys。

如果 init_sys 是 ARMAX 模型，armax 会使用 init_sys 的参数值作为估计的初始猜测。要配置 A(q)、B(q) 和 C(q) 的初始猜测和约束，请使用 init_sys 的 Structure 属性。例如：

要为 init_sys 的 A(q) 项指定初始猜测，请将 init_sys.Structure.A.Value 设置为初始猜测。
要为 init_sys 的 B(q) 项指定约束：
- 将 init_sys.Structure.B.Minimum 设置为最小 B(q) 系值。
- 将 init_sys.Structure.B.Maximum 设置为最大 B (q) 系值。
- 设置 init_sys.Structure.B.Free 来指示哪些 B (q) 系数可以自由估计。

如果 init_sys 不是具有 ARMAX 结构的多项式模型，软件会首先将 init_sys 转换为 ARMAX 模型。armax 使用结果模型的参数作为估计 sys 的初始猜测。

如果未指定 opt 且 init_sys 是通过估计获得的，则使用 init_sys.Report.OptionsUsed 中的估计选项。

有关示例，请参阅使用状态空间模型初始化 ARMAX 模型参数。

`opt` — 估计选项
`armaxOptions` 选项集

ARMAX 模型辨识的估计选项，指定为 armaxOptions 选项集。opt 指定的选项包括以下内容：

初始条件处理 - 使用此选项确定如何设置或估计初始条件。
输入和输出数目据偏移 - 使用这些选项在估计期间从数据中删除偏移。
正则化 - 使用此选项可控制估计过程中偏置和方差误差之间的权衡。

名称-值参数

全部折叠

以 Name1=Value1,...,NameN=ValueN 的形式指定可选参量对组，其中 Name 是参量名称，Value 是对应的值。名称-值参量必须出现在其他参量之后，但对各个参量对组的顺序没有要求。

如果使用的是 R2021a 之前的版本，请使用逗号分隔每个名称和值，并用引号将 Name 引起来。

示例: 'InputDelay',2 对所有输入通道应用两个采样周期的输入延迟。

`Ts` — 采样时间
`1` (默认) | 正标量

采样时间，指定为以逗号分隔的对，由 'Ts' 和以 TimeUnit 指定的单位表示的采样时间组成。当您使用基于矩阵的数据（u、y）时，如果您需要除假定的 1 秒采样时间之外的采样时间，则必须指定 Ts。

要获取时间表 tt 的数据采样时间，请使用时间表属性 tt.Properties.Timestep。

示例: armax(umat1,ymat1,___,'Ts',0.08) 计算采样时间为 0.08 秒的模型。

`InputDelay` — 输入延迟
`0` (默认) | 整数标量 | 正整数向量

输入延迟表示为采样时间的整数倍数，指定为由 'InputDelay' 和以下之一组成的逗号分隔的对：

N_u×1 向量，其中 N_u 是输入数目 - 每个条目都是一个值，表示相应输入通道的输入延迟。
标值 - 对所有输入通道应用相同的延迟。
0 - 无输入延迟。

示例: armax(data,[2 1 1 0],'InputDelay',1) 估计具有一阶 B 和 C 多项式的二阶 ARX 模型，该模型具有两个采样的输入延迟。

`IODelay` — 传输延误
`0` (默认) | 标量 | 矩阵

每个输入-输出对的传输延迟，表示为采样时间的整数倍数，并指定为由 'IODelay' 和以下之一组成的逗号分隔的对：

N_yxN_u 矩阵，其中 N_y 是输出数目，N_u 是输入数目 - 每个条目都是一个整值，表示相应输入-输出对的传输延迟。
标值 - 对所有输入-输出对应用相同的延迟。

'IODelay' 可以作为 nk 阶数的替代。您可以将 max(nk-1,0) 滞后分解为 'IODelay' 值。对于 nk > 1，armax(na,nb,nk) 等同于 armax(na,nb,1,'IODelay',nk-1)。

`IntegrateNoise` — 在噪声通道中添加积分器
`false` (默认) | 逻辑向量

在噪声通道中添加积分器，指定为以逗号分隔的对，由 'IntegrateNoise' 和长度为 N_y 的逻辑向量组成，其中 N_y 是输出数目。

将 'IntegrateNoise' 设置为 true 以获得特定输出结果

$A (q) y (t) = B (q) u (t - n k) + \frac{C (q)}{1 - q^{- 1}} e (t)$

其中 $\frac{1}{1 - q^{- 1}}$ 是噪声通道中的积分器，e(t)。

使用 'IntegrateNoise' 创建 ARIMA 或 ARIMAX 模型。

有关示例，请参阅ARIMA 模型。

输出参量

全部折叠

`sys` — ARMAX 模型
`idpoly` 对象

适合给定估计数据的 ARMAX 模型，以离散时间 idpoly 对象的形式返回。该模型是使用指定的模型阶数、延迟和估计选项创建的。

有关估计结果和所用选项的信息存储在模型的 Report 属性中。Report 具有以下字段。

报告字段	描述
`Status`	模型状态摘要，指示模型是通过构造创建的还是通过估计获得的
`Method`	使用的估计命令
`InitialCondition`	模型估计期间初始条件的处理，返回以下值之一： `'zero'` - 初始条件已设置为零。 `'estimate'` - 初始条件被视为独立的估计参数。 `'backcast'` - 使用最佳最小二乘拟合估计初始条件。此字段对于查看当估计选项集中的 `InitialCondition` 选项为 `'auto'` 时如何处理初始条件特别有用。
`Fit`	估计的定量评估，以结构体形式返回。有关这些质量度量的详细信息，请参阅Loss Function and Model Quality Metrics。该结构体具有以下字段。 `FitPercent` - 归一化均方根误差 (NRMSE)，用于衡量模型响应对估计数据的拟合度，以百分比 fitpercent = 100(1-NRMSE) 表示 `LossFcn` - 估计完成时的损失函数值 `MSE` - 均方误差 (MSE)，衡量模型响应对估计数据的拟合度 `FPE` - 模型的最终预测误差 `AIC` - 模型质量的原始赤池信息准则 (AIC) 测量 `AICc` - 小采样大小的校正 AIC `nAIC` - 归一化 AIC `BIC` - 贝叶斯信息标准 (BIC)
`Parameters`	模型参数的估计值
`OptionsUsed`	用于估计的选项集。如果没有配置自定义选项，则这是一组默认选项。请参阅 `armaxOptions` 以了解详细信息。
`RandState`	估计开始时随机数流的状态。如果在估计期间未使用随机化，则为空 `[]`。有关详细信息，请参阅 `rng`。
`DataUsed`	用于估计的数据的属性，以具有以下字段的结构返回。 `Name` - 数据集的名称 `Type` - 数据类型 `Length` - 数据采样数 `Ts` - 采样时间 `InterSample` - 输入采样间行为，以下列值之一返回： `'zoh'` - 零阶保持器在采样之间维持分段常数输入信号。 `'foh'` - 一阶保持器在采样之间维持分段线性输入信号。 `'bl'` - 带限行为指定连续时间输入信号在奈奎斯特频率以上的功率为零。 `InputOffset` - 估计期间从时域输入数目据中移除的偏移量。对于非线性模型，它是 `[]`。 `OutputOffset` - 估计期间从时域输出数目据中移除的偏移量。对于非线性模型，它是 `[]`。
`Termination`	用于预测误差最小化的迭代搜索的终止条件，以包含这些字段的结构返回。 `WhyStop` - 终止数值搜索的原因 `Iterations` - 估计算法执行的搜索迭代次数 `FirstOrderOptimality` - 搜索算法终止时梯度搜索向量的 $\infty$ -范数 `FcnCount` -目标函数被调用的次数 `UpdateNorm` - 最后一次迭代中的梯度搜索向量的范数。当搜索方法为 `'lsqnonlin'` 或 `'fmincon'` 时省略。 `LastImprovement` - 上次迭代中的标准改进，以百分比表示。当搜索方法为 `'lsqnonlin'` 或 `'fmincon'` 时省略。 `Algorithm` - `'lsqnonlin'` 或 `'fmincon'` 搜索方法使用的算法。当使用其他搜索方法时省略。对于不需要数值搜索优化的估计方法，省略了 `Termination` 字段。

有关使用 Report 的详细信息，请参阅Estimation Report。

`ic` — 初始条件
`initialCondition` 对象 | `initialCondition` 值的对象数组

估计的初始条件，以 initialCondition 对象或 initialCondition 值的对象数组形式返回。

对于单试验数据集，ic 以状态空间形式表示传递函数模型（A 和 C 矩阵）对估计的初始状态 (x₀) 的自由响应。
对于包含 N_e 个试验的多试验数据集，ic 是一个长度为 N_e 的对象数组，其中包含每个试验的一组 initialCondition 值。

如果 armax 返回 ic 的 0 值，并且您知道您具有非零初始条件，请将 armaxOptions 中的 'InitialCondition' 选项设置为 'estimate'，并将更新的选项集传递给 armax。例如：

opt = armaxOptions('InitialCondition','estimate')
[sys,ic] = armax(data,np,nz,opt)

当初始条件对整体估计误差最小化过程的影响可忽略不计时，'InitialCondition' 的默认 'auto' 设置使用 'zero' 方法。指定 'estimate' 可确保软件估计 ic 的值。

有关详细信息，请参阅 initialCondition。有关使用此参量的示例，请参阅获取初始条件。

详细信息

全部折叠

ARMAX 模型

ARMAX（带额外输入的自回归移动平均）模型结构为：

$\begin{array}{l} y (t) + a_{1} y (t - 1) + \dots + a_{n_{a}} y (t - n_{a}) = \\ b_{1} u (t - n_{k}) + \dots + b_{n_{b}} u (t - n_{k} - n_{b} + 1) + \\ c_{1} e (t - 1) + \dots + c_{n_{c}} e (t - n_{c}) + e (t) \end{array}$

更简洁的差分方程写法是

$A (q) y (t) = B (q) u (t - n_{k}) + C (q) e (t)$

其中

$y (t)$ - 时间 $t$ 的输出
$n_{a}$ - 极点数
$n_{b}$ - 零点数加 1
$n_{c}$ - 系数的数量
$n_{k}$ - 输入影响输出之前发生的输入采样数，也称为系统中的死区时间
$y (t - 1) \dots y (t - n_{a})$ - 当前输出所依赖的先前输出
$u (t - n_{k}) \dots u (t - n_{k} - n_{b} + 1)$ - 当前输出所依赖的先前输入和延迟输入
$e (t - 1) \dots e (t - n_{c})$ - 白噪声干扰值

参数 na、nb、nc 为 ARMAX 模型的阶数，nk 为延时，q 为延时算子。具体来说，

$A (q) = 1 + a_{1} q^{- 1} + \dots + a_{n_{a}} q^{- n_{a}}$

$B (q) = b_{1} + b_{2} q^{- 1} + \dots + b_{n_{b}} q^{- n_{b} + 1}$

$C (q) = 1 + c_{1} q^{- 1} + \dots + c_{n_{c}} q^{- n_{c}}$

ARMA 时间序列模型

ARMA（自回归移动平均）模型是没有输入通道的ARMAX 模型的特殊情况。ARMA 单输出模型结构由下方程给出：

$A (q) y (t) = C (q) e (t)$

ARIMAX 模型

ARIMAX（带额外输入的自回归移动平均模型）模型结构与 ARMAX 模型类似，不同之处在于它在噪声源 e(t) 中包含一个积分器：

$A (q) y (t) = B (q) u (t - n k) + \frac{C (q)}{(1 - q^{- 1})} e (t)$

ARIMA 模型

ARIMA（自回归综合移动平均线）模型结构是没有输入的 ARIMAX 模型的简化：

$A (q) y (t) = \frac{C (q)}{(1 - q^{- 1})} e (t)$

算法

迭代搜索算法最小化稳健二次预测误差标准。当下列任一情况为真时，迭代终止：

已达到最大迭代次数。
预期的改进小于指定的公差。
无法找到该标准的较低值。

您可以使用 sys.Report.Termination 获取有关停止标准的信息。

使用 armaxOptions 选项集来创建和配置影响估计结果的选项。具体来说，使用 'SearchOptions' 属性设置搜索算法属性，例如 MaxIterations 和 Tolerance。

当您没有为迭代搜索指定初始参数值作为初始模型时，它们将在特殊的四阶段 LS-IV 算法中构建。

稳健性的截止值基于 Advanced.ErrorThreshold 估计选项以及残差与初始参数估计的估计标准差。最小化期间不会重新计算截止值。默认情况下，不执行任何鲁棒性；ErrorThreshold 选项的默认值 0。

为了确保只测试与稳定预测变量相对应的模型，该算法会对预测变量进行稳定性测试。通常， $C (q)$ 和 $F (q)$ （如果适用）都必须在单位圆内全部为零。

当估计选项 'Display' 为 'On' 或 'Full' 时，屏幕上会显示最小化信息。当 'Display' 为 'Full' 时，当前和之前的参数估计值都以列向量形式显示，并且参数按字母顺序列出。此外，还给出了标准函数（成本）的值，并显示了高斯-牛顿向量及其范数。当 'Display' 为 'On' 时，仅显示标准值。

备选方法

armax 不支持连续时间模型估计。使用 tfest 估计连续时间传递函数模型，或使用 ssest 估计连续时间状态空间模型。

armax 仅支持时域数据。对于频域数据，使用 oe 来估计输出-误差 (OE) 模型。

参考

[1] Ljung, L. System Identification: Theory for the User, Second Edition. Upper Saddle River, NJ: Prentice-Hall PTR, 1999. See chapter about computing the estimate.

版本历史记录

在 R2006a 中推出

全部展开

R2022b: 接受时间表和矩阵形式的时域估计数据

现在，大多数估计、验证、分析和实用工具函数都接受时域输入/输出数目据，其形式为包含输入和输出数目据的单个时间表或分别包含输入和输出数目据的一对矩阵。这些函数仍然接受 iddata 对象作为数据源，无论是时域数据还是频域数据。

R2018a: 当 `SearchMethod` 为 `'lsqnonlin'` 时，`SearchOptions` 的高级选项已弃用

与 lsqnonlin 相关的高级选项的设定已被弃用，包括在 Optimization Toolbox™ 中使用 lsqnonlin 搜索方法或求解器进行估计时调用并行处理的选项。

另请参阅

armaxOptions | arx | bj | oe | polyest | ssest | tfest | idpoly | iddata | compare | aic | fpe

armax

语法

说明

估计 ARMAX 或 ARMA 模型

配置初始参数

指定其他估计选项

返回估计的初始条件

示例

估计 ARMAX 模型

ARMA 模型

指定估计选项

具有正则化的 ARMAX 模型

ARIMA 模型

迭代估计 ARMAX 模型

使用状态空间模型初始化 ARMAX 模型参数

获取初始条件

输入参数

tt — 基于时间表的估计数据 时间表 | 时间表的元胞数组。

u, y — 基于矩阵的估计数据 矩阵 | 由矩阵组成的元胞数组

data — 时域估计数据 iddata 对象

[na nb nc nk] — 多项式阶数 整数行向量 | 整数矩阵的行向量 | 标量

init_sys — 用于配置初始参数化的系统 离散时间线性模型

opt — 估计选项 armaxOptions 选项集

名称-值参数

Ts — 采样时间 1 (默认) | 正标量

InputDelay — 输入延迟 0 (默认) | 整数标量 | 正整数向量

IODelay — 传输延误 0 (默认) | 标量 | 矩阵

IntegrateNoise — 在噪声通道中添加积分器 false (默认) | 逻辑向量

输出参量

sys — ARMAX 模型 idpoly 对象

ic — 初始条件 initialCondition 对象 | initialCondition 值的对象数组

详细信息

ARMAX 模型

ARMA 时间序列模型

ARIMAX 模型

ARIMA 模型

算法

备选方法

参考

版本历史记录

R2022b: 接受时间表和矩阵形式的时域估计数据

R2018a: 当 SearchMethod 为 'lsqnonlin' 时，SearchOptions 的高级选项已弃用

另请参阅

主题

`tt` — 基于时间表的估计数据
时间表 | 时间表的元胞数组。

`u`, `y` — 基于矩阵的估计数据
矩阵 | 由矩阵组成的元胞数组

`data` — 时域估计数据
`iddata` 对象

`[na nb nc nk]` — 多项式阶数
整数行向量 | 整数矩阵的行向量 | 标量

`init_sys` — 用于配置初始参数化的系统
离散时间线性模型

`opt` — 估计选项
`armaxOptions` 选项集

`Ts` — 采样时间
`1` (默认) | 正标量

`InputDelay` — 输入延迟
`0` (默认) | 整数标量 | 正整数向量

`IODelay` — 传输延误
`0` (默认) | 标量 | 矩阵

`IntegrateNoise` — 在噪声通道中添加积分器
`false` (默认) | 逻辑向量

`sys` — ARMAX 模型
`idpoly` 对象

`ic` — 初始条件
`initialCondition` 对象 | `initialCondition` 值的对象数组

R2018a: 当 `SearchMethod` 为 `'lsqnonlin'` 时，`SearchOptions` 的高级选项已弃用