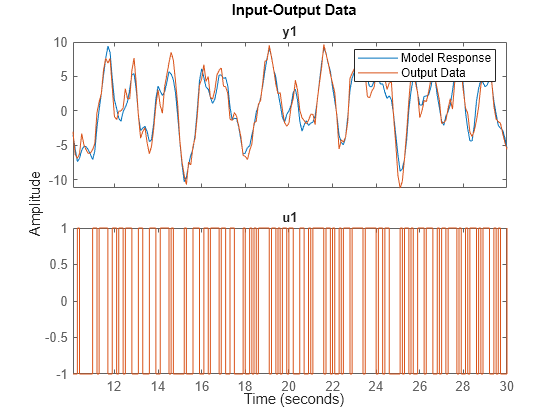
tfest
估计传递函数模型
语法
说明
估计传递函数模型
sys = tfest(u,y,np)u、y 中的时域输入信号和输出信号估计连续时间传递函数。软件假设数据采样时间为 1 秒。您无法更改此假定的采样时间。如果您想根据采样时间不是 1 秒的数据来估计模型,则有两种选择:
通过使用
'Ts'名称-值参量设置采样时间来估计离散时间系统。例如,sys = tfest(u,y,np,'Ts',0.1)将采样时间设置为0.1。您可以将此语法与 SISO、MISO 和 MIMO 系统一起使用。在估计连续时间系统之前,将矩阵数据转换为
timetable或iddata对象。这些格式允许您将采样时间知识合并到数据中。有关详细信息,请参阅u、y。
不建议根据基于矩阵的数据估计连续时间模型。
sys = tfest(___,Name,Value)sys = tfest(um,ym,np,'Ts',0.1) 从采样时间为 0.1 的矩阵数据指定离散时间系统。使用 sys = tfest(data,np,nz,'InputNames',["u1","u2"],'OutputNames',["y1","y3"]) 指定与用于 MIMO 时间表数据的变量相对应的输入和输出信号变量名称。
配置初始参数
指定其他估计选项
返回估计的初始条件
[ 将估计的初始条件作为 sys,ic] = tfest(___)initialCondition 对象返回。如果您计划使用相同的估计输入数目据来仿真或预测模型响应,然后将响应与相同的估计输出数目据进行比较,请使用此语法。结合初始条件,可以在仿真的早期阶段使测量数据与仿真或预测数据更好地匹配。
示例
输入参数
名称-值参数
输出参量
算法
参考
[1] Garnier, H., M. Mensler, and A. Richard. “Continuous-Time Model Identification from Sampled Data: Implementation Issues and Performance Evaluation.” International Journal of Control 76, no. 13 (January 2003): 1337–57. https://doi.org/10.1080/0020717031000149636.
[2] Ljung, Lennart. “Experiments with Identification of Continuous Time Models.” IFAC Proceedings Volumes 42, no. 10 (2009): 1175–80. https://doi.org/10.3182/20090706-3-FR-2004.00195.
[3] Young, Peter, and Anthony Jakeman. “Refined Instrumental Variable Methods of Recursive Time-Series Analysis Part III. Extensions.” International Journal of Control 31, no. 4 (April 1980): 741–64. https://doi.org/10.1080/00207178008961080.
[4] Drmač, Z., S. Gugercin, and C. Beattie. “Quadrature-Based Vector Fitting for Discretized H2 Approximation.” SIAM Journal on Scientific Computing 37, no. 2 (January 2015): A625–52. https://doi.org/10.1137/140961511.
[5] Ozdemir, Ahmet Arda, and Suat Gumussoy. “Transfer Function Estimation in System Identification Toolbox via Vector Fitting.” IFAC-PapersOnLine 50, no. 1 (July 2017): 6232–37. https://doi.org/10.1016/j.ifacol.2017.08.1026.
版本历史记录
在 R2012a 中推出另请参阅
tfestOptions | idtf | timetable | ssest | procest | ar | arx | oe | bj | polyest | greyest
主题
- 在命令行估计传递函数模型
- Estimate Transfer Function Models with Transport Delay to Fit Given Frequency-Response Data
- Estimate Transfer Function Models with Prior Knowledge of Model Structure and Constraints
- Apply Initial Conditions When Simulating Identified Linear Models
- Troubleshoot Frequency-Domain Identification of Transfer Function Models
- 什么是传递函数模型?
- Regularized Estimates of Model Parameters
- Estimating Models Using Frequency-Domain Data