bj
Estimate Box-Jenkins polynomial model using time-domain data
Syntax
Description
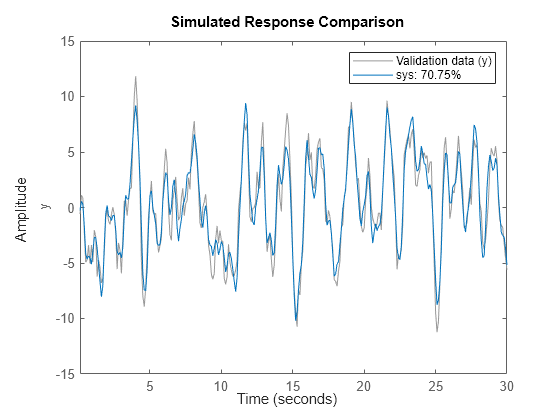
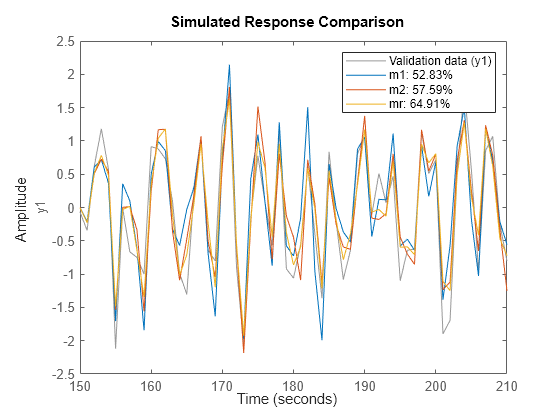
Box-Jenkins (BJ) models are a special configuration of polynomial models that provide completely independent parameterization for the dynamics and noise using rational polynomial functions. BJ models, which are always discrete-time models, can be estimated only from time-domain data. Use BJ models when the noise is primarily a measurement disturbance rather than an input disturbance. The BJ structure provides additional flexibility for modeling the noise.
Estimate Box-Jenkins Model
sys = bj(tt,[nb
nc nd nf nk])sys using the data
contained in the variables of timetable tt. The software
uses the first Nu variables as inputs and the next
Ny variables as outputs, where Nu and
Ny are determined from the dimensions of the specified
polynomial orders.
sys is represented by the equation
Here, y(t) is the output, u(t) is the input, and e(t) is the error.
The components of [nb nc nd nf nk] define the orders of
the polynomials used for estimation. For more information about the Box-Jenkins
model structure, see Box-Jenkins Model Structure.
To select specific input and output channels from tt, use
name-value syntax to set 'InputName' and
'OutputName' to the corresponding timetable variable
names.
sys = bj(u,y,[nb nc nd nf nk])u,y. The software assumes that the
data sample time is 1 second. To change the sample time, set
Ts using name-value syntax.
sys = bj(data,[nb nc nd nf nk])iddata object
data. Use this syntax especially when you want to take
advantage of the additional information, such as data sample time or experiment
labeling, that data objects provide.
sys = bj(___, Name,Value)
Configure Initial Parameters
Specify Additional Estimation Options
Return Estimated Initial Conditions
[
returns the estimated initial conditions as an sys,ic] = bj(___)initialCondition object. Use this syntax if you plan to simulate
or predict the model response using the same estimation input data and then
compare the response with the same estimation output data. Incorporating the
initial conditions yields a better match during the first part of the
simulation.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
More About
Alternatives
To estimate a continuous-time model, use:
References
[1] Ljung, L. System Identification: Theory for the User, Upper Saddle River, NJ, Prentice-Hall PTR, 1999.